You do not have permission to view this page - please try signing in.

6.P: Exercises

Last updated

Oct 1, 2019
Save as PDF
- 4.7: Looking Back and Ahead
- 11.2: Spin Resonance

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Calculate the Clebsch-Gordon coefficients for adding spin one-half to spin one.
Calculate the Clebsch-Gordon coefficients for adding spin one to spin one.
An electron in a hydrogen atom occupies the combined spin and position state whose wavefunction is
$\psi = R_{2\,1}(r)\,\left[\sqrt{1/3}\,Y_{1\,0}(\theta,\varphi)\,\chi_+ + \sqrt{2/3}\,Y_{1\,1}(\theta,\varphi)\,\chi_-\right].$
1. What values would a measurement of $L^2$ yield, and with what probabilities?
2. Same for $S^2$ .
3. Same for $J^{\,2}$ .
4. Same for $r$ , $\varphi$ ?
5. What is the probability density for finding the electron in the spin up state (with respect to the $r$ ?
In a low energy neutron-proton system (with zero orbital angular momentum) the potential energy is given by
$V({\bf x}) = V_1(r) + V_2(r)\left[3\,\frac{(\mbox{\boldmath $\sig... ...\right] + V_3(r)\,\mbox{\boldmath $\sigma$}_n\cdot\mbox{\boldmath $\sigma$}_p,$
where $\sigma$ $\sigma$ $V({\bf x})$ with respect to the overall spin state.]
Consider two electrons in a spin singlet (i.e., spin zero) state.
1. If a measurement of the spin of one of the electrons shows that it is in the state with $z$ -component of the spin of the other electron yields $S_y=\hbar/2$ , what is the probability that a measurement of the $S_x=-\hbar/2$ ?
2. Finally, if electron 1 is in a spin state described by 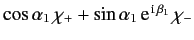$\cos\alpha_1\,\chi_+ + \sin\alpha_1\,{\rm e}^{\,{\rm i}\,\beta_1}\,\chi_-$ , and electron 2 is in a spin state described by 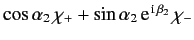$\cos\alpha_2\,\chi_+ + \sin\alpha_2\,{\rm e}^{\,{\rm i}\,\beta_2}\,\chi_-$ , what is the probability that the two-electron spin state is a triplet (i.e., spin one) state?

Contributors

Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

$\newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$

Search

Text Color

Text Size

Margin Size

Font Type

Contributors

Support Center

How can we help?