7.4: Quadratic Stark Effect

Suppose that a one-electron atom [i.e., either a hydrogen atom, or an alkali metal atom (which possesses one valance electron orbiting outside a closed, spherically symmetric, shell)] is subjected to a uniform electric field in the positive $z$ -direction. The Hamiltonian of the system can be split into two parts. The unperturbed Hamiltonian,

$H_0 = \frac{{p}^2}{2\,m_e} + V(r),$ $\ref{617}$

and the perturbing Hamiltonian,

$H_1= e\, \vert{\bf E}\vert\, z.$ $\ref{618}$

Here, we are neglecting the small difference between the reduced mass, $\mu$ , and the electron mass, $m_e$ .

It is assumed that the unperturbed energy eigenvalues and eigenstates are completely known. The electron spin is irrelevant in this problem (because the spin operators all commute with $H_1$ ), so we can ignore the spin degrees of freedom of the system. This implies that the system possesses no degenerate energy eigenvalues. Actually, this is not true for the $n\neq 1$ energy levels of the hydrogen atom, due to the special properties of a pure Coulomb potential. It is necessary to deal with this case separately, because the perturbation theory presented in Section 7.3 breaks down for degenerate unperturbed energy levels.

An energy eigenket of the unperturbed Hamiltonian is characterized by three quantum numbers--the radial quantum number $n$ , and the two angular quantum numbers $l$ and $m$ (see Section 4.6). Let us denote such a ket $\vert n,l,m\rangle$ , and let its energy be $E_{nlm}$ . According to Equation $\ref{614}$, the change in this energy induced by a small electric field is given by

$\ref{619}$

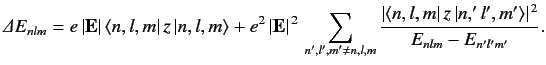
Now, since

$L_z = x\,p_y - y\, p_x,$ $\ref{620}$

it follows that

$[L_z, z] = 0.$ $\ref{621}$

Thus,

$\langle n,l, m\vert\, [L_z, z]\, \vert n',l',m'\rangle = 0,$ $\ref{622}$

giving

$(m - m')\, \langle n,l, m\vert\,z\,\vert n',l',m'\rangle = 0,$ $\ref{623}$

because $\vert n,l,m\rangle$ is, by definition, an eigenstate of $L_z$ with eigenvalue $m\,\hbar$ . It is clear, from the above relation, that the matrix element $\langle n,l, m\vert\,z\,\vert n',l',m'\rangle$ is zero unless $m'=m$ . This is termed the selection rule for the quantum number $m$ .

Let us now determine the selection rule for $l$ . We have

$[L^2, z]$ $= [L_x^{\,2}, z] + [L_y^{\,2}, z] = L_x\,[L_x, z] + [L_x, z] \,L_x + L_y\,[L_y, z] + [L_y, z]\, L_y$ $= {\rm i}\,\hbar\left( -L_x\, y - y\, L_x + L_y \,x + x \,L_y\right)= 2 \,{\rm i} \, \hbar \,( L_y \,x - L_x \,y + {\rm i}\,\hbar\,z)$ $= 2 \,{\rm i}\, \hbar \,( L_y\, x - y \,L_x ) = 2\, {\rm i}\, \hbar\, ( x\, L_y - L_x \,y),$ $\ref{624}$

where use has been made of Equations $\ref{290}$-$\ref{295}$. Similarly,

$[L^2, y]$ $= 2\,{\rm i}\, \hbar \,( L_x\, z - x\, L_z ),$ $\ref{625}$ $[L^2, x]$ $= 2\,{\rm i}\, \hbar\, ( y \,L_z - L_y \,z).$ $\ref{626}$

Thus,

$[L^2, [L^2, z]]$ $= - 4\, \hbar^2 \,L_y\,(y\, L_z - L_y \,z) + 4\,\hbar^2 \,L_x\,(L_x\, z - x\, L_z)- 2\, \hbar^2\,(L^2 \,z - z\, L^2).$ $\ref{627}$

This reduces to

$\ref{628}$

However, it is clear from Equations $\ref{290}$-$\ref{292}$ that

$L_x \,x + L_y \,y + L_z \,z = 0.$ $\ref{629}$

Hence, we obtain

$[L^2, [L^2, z]] = 2 \,\hbar^2\, (L^2\, z + z \,L^2),$ $\ref{630}$

which can be expanded to give

$L^4 \,z - 2\, L^2 \,z\, L^2 + z\, L^4 - 2\, \hbar^2\, (L^2 \,z +z \,L^2) = 0.$ $\ref{631}$

Equation $\ref{631}$ implies that

$\langle n,l,m\vert\, L^4\, z - 2\, L^2\, z \,L^2 + z\, L^4 - 2 \,\hbar^2 \,(L^2\, z +z\, L^2)\, \vert n',l',m' \rangle = 0.$ $\ref{632}$

This expression yields

$\ref{633}$

which reduces to

$(l+l'+2)\,(l+l')\,(l-l'+1)\,(l-l'-1)\,\langle n,l,m\vert\,z\,\vert n',l',m' \rangle = 0.$ $\ref{634}$

According to the above formula, the matrix element $\langle n,l, m\vert\,z\,\vert n',l',m'\rangle$ vanishes unless $l=l'=0$ or $l' = l\pm 1$ . This matrix element can be written

$\ref{635}$

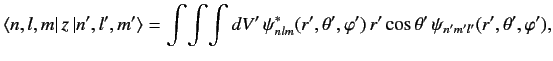
where $\psi_{nlm}({\bf x}') = \langle {\bf x}'\vert n,l,m\rangle$ . Recall, however, that the wavefunction of an $l=0$ state is spherically symmetric (see Section 4.3): i.e., $\psi_{n00}({\bf x}') = \psi_{n00}(r')$ . It follows from Equation $\ref{635}$ that the matrix element vanishes by symmetry when $l=l'=0$ . In conclusion, the matrix element $\langle n,l, m\vert\,z\,\vert n',l',m'\rangle$ is zero unless $l' = l\pm 1$ . This is the selection rule for the quantum number $l$ .

Application of the selection rules to Equation $\ref{619}$ yields

$\ref{636}$

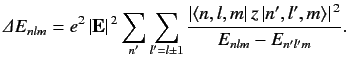
Note that all of the terms in Equation $\ref{619}$ that vary linearly with the electric field-strength vanish by symmetry, according to the selection rules. Only those terms that vary quadratically with the field-strength survive. The electrical polarizability, $\alpha$ , of an atom is defined in terms of the electric-field induced energy-shift of a given atomic state as follows:

${\mit\Delta} E = - \frac{1}{2} \,\alpha \,\vert{\bf E}\vert^{\,2}.$ $\ref{637}$

Consider the ground state of a hydrogen atom. (Recall, that we cannot address the $n>1$ excited states because they are degenerate, and our theory cannot handle this at present). The polarizability of this state is given by

$\alpha = 2 \,e^2 \sum_{n>1} \frac{\vert\langle 1,0,0\vert\,z\,\vert n,1,0\rangle\vert^{\,2}}{E_{n00}-E_{100}}.$ $\ref{638}$

Here, we have made use of the fact that $E_{n10} = E_{n00}$ for a hydrogen atom.

The sum in the above expression can be evaluated approximately by noting that [see Equation $\ref{409}$]

$E_{n00} = - \frac{e^2}{8\pi\,\epsilon_0\, a_0\,n^2}$ $\ref{639}$

for a hydrogen atom, where

$a_0 = \frac{4\pi \,\epsilon_0 \,\hbar^2}{m_e \,e^2}$ $\ref{640}$

is the Bohr radius. We can write

$E_{n00}-E_{100} \geq E_{200} - E_{100} = \frac{3}{4} \frac{e^2}{8\pi\,\epsilon_0\, a_0}.$ $\ref{641}$

Thus,

$\alpha < \frac{16}{3}\, 4\pi \,\epsilon_0\, a_0 \sum_{n>1} \vert\langle 1,0,0\vert\,z\,\vert n,1,0\rangle\vert^{\,2}.$ $\ref{642}$

However,

$\ref{643}$

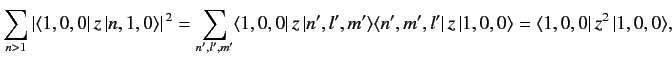
where we have made use of the fact that the wavefunctions of a hydrogen atom form a complete set. It is easily demonstrated from the actual form of the ground-state wavefunction that

$\langle 1,0,0\vert\,z^2\,\vert 1,0,0\rangle = a_0^{\,2}.$ $\ref{644}$

Thus, we conclude that

$\alpha < \frac{16}{3} \,4\pi\, \epsilon_0\, a_0^{\,3} \simeq 5.3\,4\pi\, \epsilon_0 \,a_0^{\,3}.$ $\ref{645}$

The exact result is

$\alpha = \frac{9}{2}\, 4\pi\, \epsilon_0\, a_0^{\,3} = 4.5\,4\pi \,\epsilon_0 \,a_0^{\,3}.$ $\ref{646}$

It is possible to obtain this result, without recourse to perturbation theory, by solving Schrödinger's equation in parabolic coordinates.

Contributors

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  $\newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$