Skip to main content
\(\require{cancel}\)
Physics LibreTexts

8.6: Sudden Perturbations

  1. Last updated
    08:37, 16 Nov 2014
  2. Save as PDF

Consider, for example, a constant perturbation that is suddenly switched on at time $ t=0$ :

 

$\displaystyle H_1(t)$ $\displaystyle = 0$   $\displaystyle \mbox{\hspace{2.0cm}for $t<0$}$    
$\displaystyle H_1(t)$ $\displaystyle = H_1$$\displaystyle \mbox{\hspace{1.75cm}for $t\geq 0$}$$\displaystyle ,$ (801)

 

 

where $ H_1$ is time-independent, but is generally a function of the position, momentum, and spin operators. Suppose that the system is definitely in state $ \vert i\rangle$ at time $ t=0$ . According to Equations (795)-(797) (with $ t_0=0$ ),

 

$\displaystyle c_n^{(0)}(t)$ $\displaystyle = \delta_{i\,n},$ (802)
$\displaystyle c_n^{(1)}(t)$ $\displaystyle = -\frac{{\rm i}}{\hbar}\, H_{ni} \int_0^t dt'\,\exp[\,{\rm i}\, ... ...{ni}\,(t'-t)]= \frac{H_{ni}}{E_n - E_i}\, [1- \exp(\,{\rm i}\,\omega_{ni}\,t)],$ (803)

 

 

giving

 

$\displaystyle P_{i\rightarrow n}(t) \simeq \vert c_n^{(1)}\vert^{\,2} = \frac{4... ...vert E_n - E_i\vert^{\,2}}\, \sin^2\left[ \frac{(E_n-E_i)\,t}{2\,\hbar}\right],$ (804)

 

 

for $ i\neq n$ . The transition probability between states $ \vert i\rangle$ and $ \vert n\rangle$ can be written

 

$\displaystyle P_{i\rightarrow n}(t) = \frac{\vert H_{ni}\vert^{\,2} \,t^2}{\hbar^2} \,{\rm sinc}^2\left[ \frac{(E_n-E_i)\,t}{2\,\hbar}\right],$ (805)

 

 

where

 

$\displaystyle {\rm sinc}(x)\equiv \frac{\sin x}{x}.$ (806)

 

 

The sinc function is highly oscillatory, and decays like $ 1/\vert x\vert$ at large $ \vert x\vert$ . It is a good approximation to say that $ {\rm sinc}(x)$ is small except when $ \vert x\vert \stackrel {_{\normalsize <}}{_{\normalsize\sim}}\pi$ . It follows that the transition probability, $ P_{i\rightarrow n}$ , is small except when

 

$\displaystyle \vert E_n - E_i\vert \stackrel {_{\normalsize <}}{_{\normalsize\sim}}\frac{2\pi\, \hbar}{t}.$ (807)

 

 

Note that in the limit $ t\rightarrow \infty$ only those transitions that conserve energy (i.e., $ E_n=E_i$ ) have an appreciable probability of occurrence. At finite $ t$ , is is possible to have transitions which do not exactly conserve energy, provided that

 

$\displaystyle {\mit\Delta} E \,{\mit\Delta} t \stackrel {_{\normalsize <}}{_{\normalsize\sim}}h,$ (808)

 

 

where $ {\mit\Delta} E = \vert E_n - E_i\vert$ is the change in energy of the system associated with the transition, and $ {\mit\Delta} t = t$ is the time elapsed since the perturbation was switched on. This result is just a manifestation of the well-known uncertainty relation for energy and time. Incidentally, the energy-time uncertainty relation is fundamentally different to the position-momentum uncertainty relation, because (in non-relativistic quantum mechanics) position and momentum are operators, whereas time is merely a parameter.

The probability of a transition that conserves energy (i.e., $ E_n=E_i$ ) is

 

$\displaystyle P_{i\rightarrow n} (t) = \frac{\vert H_{in}\vert^{\,2}\,t^2}{\hbar^2},$ (809)

 

 

where use has been made of $ {\rm sinc}(0) = 1$ . Note that this probability grows quadratically with time. This result is somewhat surprising, because it implies that the probability of a transition occurring in a fixed time interval, $ t$ to $ t+dt$ , grows linearly with $ t$ , despite the fact that $ H_1$ is constant for $ t>0$ . In practice, there is usually a group of final states, all possessing nearly the same energy as the energy of the initial state $ \vert i\rangle$ . It is helpful to define the density of states, $ \rho(E)$ , where the number of final states lying in the energy range $ E$ to $ E+dE$ is given by $ \rho(E)\,dE$ . Thus, the probability of a transition from the initial state $ i$ to any of the continuum of possible final states is

 

$\displaystyle P_{i\rightarrow} (t) = \int dE_n\,P_{i\rightarrow n}(t) \,\rho(E_n),$ (810)

 

 

giving

 

$\displaystyle P_{i\rightarrow} (t) = \frac{2\, t}{\hbar} \int dx\, \vert H_{ni}\vert^{\,2}\, \rho(E_n) \,{\rm sinc}^2(x),$ (811)

 

 

where

 

$\displaystyle x=(E_n-E_i)\,t/2\,\hbar,$ (812)

 

 

and use has been made of Equation (805). We know that in the limit $ t\rightarrow \infty$ the function $ {\rm sinc}(x)$ is only non-zero in an infinitesimally narrow range of final energies centered on $ E_n=E_i$ . It follows that, in this limit, we can take $ \rho(E_n)$ and $ \vert H_{ni}\vert^{\,2}$ out of the integral in the above formula to obtain

 

$\displaystyle P_{i\rightarrow[n]} (t) = \left.\frac{2\pi}{\hbar}\, \overline{\vert H_{ni}\vert^{\,2}} \,\rho(E_n)\,t\, \right\vert _{E_n\simeq E_i},$ (813)

 

 

where $ P_{i\rightarrow [n]}$ denotes the transition probability between the initial state $ \vert i\rangle$ and all final states $ \vert n\rangle$ that have approximately the same energy as the initial state. Here, $ \overline{\vert H_{ni}\vert^{\,2}}$ is the average of $ \vert H_{ni}\vert^{\,2}$ over all final states with approximately the same energy as the initial state. In deriving the above formula, we have made use of the result

 

$\displaystyle \int_{-\infty}^{\infty} dx\,\,{\rm sinc}^2(x) = \pi.$ (814)

 

 

Note that the transition probability, $ P_{i\rightarrow [n]}$ , is now proportional to $ t$ , instead of $ t^2$ .

It is convenient to define the transition rate, which is simply the transition probability per unit time. Thus,

 

$\displaystyle w_{i\rightarrow [n]} = \frac{d P_{i\rightarrow [n]}}{dt},$ (815)

 

 

giving

 

$\displaystyle w_{i\rightarrow [n]} = \left.\frac{2\pi}{\hbar}\, \overline{\vert H_{ni}\vert^{\,2}} \,\rho(E_n) \right\vert _{E_n\simeq E_i}.$ (816)

 

 

This appealingly simple result is known as Fermi's golden rule. Note that the transition rate is constant in time (for $ t>0$ ): i.e., the probability of a transition occurring in the time interval $ t$ to $ t+dt$ is independent of $ t$ for fixed $ dt$ . Fermi's golden rule is sometimes written

 

$\displaystyle w_{i\rightarrow n} = \frac{2\pi}{\hbar} \,\vert H_{ni}\vert^{\,2}\, \delta(E_n - E),$ (817)

 

 

where it is understood that this formula must be integrated with $ \int dE_n\,\rho(E_n)$ to obtain the actual transition rate.

Let us now calculate the second-order term in the Dyson series, using the constant perturbation (801). From Equation (797) we find that

 

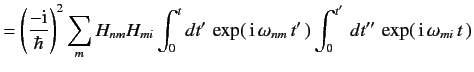
$\displaystyle c_n^{(2)}(t)$ $\displaystyle = \left(\frac{-{\rm i}}{\hbar}\right)^2 \sum_m H_{nm} H_{mi} \int... ...i}\,\omega_{nm}\,t'\,) \int_0^{t'} \, dt'' \,\exp(\,{\rm i} \,\omega_{mi}\,t\,)$    
  $\displaystyle =\frac{\rm i}{\hbar} \sum_m \frac{H_{nm} \,H_{mi}}{E_m - E_i} \in... ...[\exp(\,{\rm i}\,\omega_{ni}\,t'\,) - \exp(\,{\rm i}\,\omega_{nm}\,t']\,\right)$    
  $\displaystyle = \frac{{\rm i}\,t}{\hbar} \sum_m \frac{H_{nm} H_{mi}}{E_m - E_i}... ...t/2)- \exp(\,{\rm i}\,\omega_{nm} \,t/2) \,{\rm sinc}(\omega_{nm}\,t/2)\right].$ (818)

 

 

Thus,

 

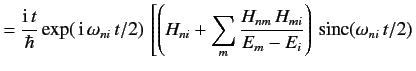$\displaystyle c_n(t) = c_n^{(1)}+ c_n^{(2)}$ $\displaystyle = \frac{{\rm i}\,t}{\hbar} \exp(\,{\rm i}\,\omega_{ni}\,t/2)\, \l... ... \frac{H_{nm}\,H_{mi}}{E_m - E_i}\right)\, {\rm sinc} (\omega_{ni}\,t/2)\right.$    
  $\displaystyle \left. - \sum_m\frac{H_{nm}\,H_{mi}}{E_m - E_i} \exp(\,{\rm i}\,\omega_{im}\,t/2)\,{\rm sinc}(\omega_{nm}\,t/2)\right],$ (819)

 

 

where use has been made of Equation (803). It follows, by analogy with the previous analysis, that

 

$\displaystyle w_{i\rightarrow [n]} =\left. \frac{2\pi}{\hbar}\, \overline{ \lef... ...\,H_{mi}}{E_m - E_i}\right\vert^{\,2}} \rho(E_n) \right\vert _{E_n \simeq E_i},$ (820)

 

 

where the transition rate is calculated for all final states, $ \vert n\rangle$ , with approximately the same energy as the initial state, $ \vert i\rangle$ , and for intermediate states, $ \vert m\rangle$ whose energies differ from that of the initial state. The fact that $ E_m\neq E_i$ causes the last term on the right-hand side of Equation (819) to average to zero (due to the oscillatory phase-factor) during the evaluation of the transition probability.

According to Equation (820), a second-order transition takes place in two steps. First, the system makes a non-energy-conserving transition to some intermediate state $ \vert m\rangle$ . Subsequently, the system makes another non-energy-conserving transition to the final state $ \vert n\rangle$ . The net transition, from $ \vert i\rangle$ to $ \vert n\rangle$ , conserves energy. The non-energy-conserving transitions are generally termed virtual transitions, whereas the energy conserving first-order transition is termed a real transition. The above formula clearly breaks down if $ H_{nm}\,H_{mi}\neq 0$ when $ E_m = E_i$ . This problem can be avoided by gradually turning on the perturbation: i.e., $ H_1\rightarrow \exp(\eta\,t)\, H_1$ (where $ \eta$ is very small). 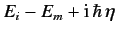The net result is to change the energy denominator in Equation (820) from $ E_i-E_m$ to $ E_i - E_m +{\rm i}\,\hbar\,\eta$ .

Contributors