8.7: Energy-Shifts and Decay-Widths
- Page ID
- 1232
We have examined how a state \( \vert n\rangle\) , other than the initial state \( \vert i\rangle\) , becomes populated as a result of some time-dependent perturbation applied to the system. Let us now consider how the initial state becomes depopulated.
In this case, it is convenient to gradually turn on the perturbation from zero at \( t=-\infty\) . Thus,
where \( \eta\) is small and positive, and \( H_1\) is a constant.
In the remote past, \( t\rightarrow -\infty\) , the system is assumed to be in the initial state \( \vert i\rangle\) . Thus, \( c_i(t\rightarrow-\infty) =1\) , and \( c_{n\neq i}(t\rightarrow -\infty) = 0\) . Basically, we want to calculate the time evolution of the coefficient \( c_i(t)\) . First, however, let us check that our previous Fermi golden rule result still applies when the perturbing potential is turned on slowly, instead of very suddenly. For \( c_{n \neq i}(t)\) we have from Equations \ref{795}-\ref{796} that
![$ = - \frac{\rm i}{\hbar}\, H_{ni} \int_{-\infty}^t dt'\, \exp[(\et...
..., \frac{ \exp[(\eta + {\rm i}\,\omega_{ni} )\, t]}{\eta +{\rm i}\,\omega_{ni}},$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1950.png)
where \( H_{ni} = \langle n\vert\,H_1\,\vert i\rangle\) . It follows that, to first order, the transition probability from state \( \vert i\rangle\) to state \( \vert n\rangle\) is
The transition rate is given by
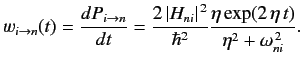
Consider the limit \( \eta\rightarrow 0\) . In this limit, \( \exp(\eta\, t)\rightarrow 1\) , but
Thus, Equation \ref{825} yields the standard Fermi golden rule result
It is clear that the delta-function in the above formula actually represents a function that is highly peaked at some particular energy. The width of the peak is determined by how fast the perturbation is switched on.
Let us now calculate \( c_i(t)\) using Equations \ref{795}-\ref{797}. We have
![$ = \left(\frac{-{\rm i}}{\hbar} \right)^2 \sum_m \vert H_{mi}\vert...
...xp[(\eta+ {\rm i}\,\omega_{im})\, t'] \exp[ (\eta+ {\rm i}\,\omega_{mi})\, t'']$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1962.png)
Thus, to second order we have
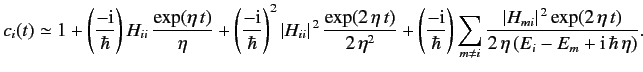
Let us now consider the ratio \( \dot{c_i}/c_i\) , where ![]() . Using Equation \ref{831}, we can evaluate this ratio in the limit \( \eta\rightarrow 0\) . We obtain
. Using Equation \ref{831}, we can evaluate this ratio in the limit \( \eta\rightarrow 0\) . We obtain
![$ \simeq \left[\left( \frac{-{\rm i}}{\hbar}\right) H_{ii} + \left(...
...a}\right]\left/\left( 1- \frac{\rm i}{\hbar} \frac{H_{ii}}{\eta} \right)\right.$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1968.png)
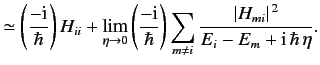
This result is formally correct to second order in perturbed quantities. Note that the right-hand side of Equation \ref{832} is independent of time. We can write
where
is a constant. According to a well-known result in pure mathematics,
where \( \epsilon >0\) , and \( {\cal P}\) denotes the principal part. It follows that
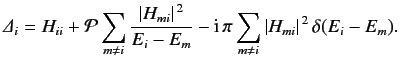
It is convenient to normalize the solution of Equation \ref{833} such that \( c_i\ref{0} = 1\) . Thus, we obtain
According to Equation \ref{744}, the time evolution of the initial state ket \( \vert i\rangle\) is given by
We can rewrite this result as
It is clear that the real part of \( {\mit\Delta}_i\) gives rise to a simple shift in energy of state \( \vert i\rangle\) , whereas the imaginary part of \( {\mit\Delta}_i\) governs the growth or decay of this state. Thus,
where
and
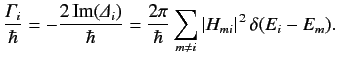
Note that the energy-shift \( {\mit\Delta} E_i\) is the same as that predicted by standard time-independent perturbation theory.
The probability of observing the system in state \( \vert i\rangle\) at time \( t>0\) , given that it is definately in state \( \vert i\rangle\) at time \( t=0\) , is given by
where
Here, use has been made of Equation \ref{817}. Clearly, the rate of decay of the initial state is a simple function of the transition rates to the other states. Note that the system conserves probability up to second order in perturbed quantities, because
The quantity \( {\mit\Gamma}_i\) is called the decay-width of state \( \vert i\rangle\) . It is closely related to the mean lifetime of this state,
where
According to Equation \ref{839}, the amplitude of state \( \vert i\rangle\) both oscillates and decays as time progresses. Clearly, state \( \vert i\rangle\) is not a stationary state in the presence of the time-dependent perturbation. However, we can still represent it as a superposition of stationary states (whose amplitudes simply oscillate in time). Thus,
where \( f(E)\) is the weight of the stationary state with energy \( E\) in the superposition. The Fourier inversion theorem yields
In the absence of the perturbation, \( \vert f(E)\vert^{\,2}\) is basically a delta-function centered on the unperturbed energy \( E_i\) of state \( \vert i\rangle\) . In other words, state \( \vert i\rangle\) is a stationary state whose energy is completely determined. In the presence of the perturbation, the energy of state \( \vert i\rangle\) is shifted by \( {\rm Re}({\mit\Delta}_i)\) . The fact that the state is no longer stationary (i.e., it decays in time) implies that its energy cannot be exactly determined. Indeed, the energy of the state is smeared over some region of width (in energy) \( {\mit\Gamma}_i\) centered around the shifted energy \( E_i +{\rm Re}({\mit\Delta}_i)\) . The faster the decay of the state (i.e., the larger \( {\mit\Gamma}_i\) ), the more its energy is spread out. This effect is clearly a manifestation of the energy-time uncertainty relation \( {\mit\Delta} E\, {\mit\Delta} t \sim \hbar\) . One consequence of this effect is the existence of a natural width of spectral lines associated with the decay of some excited state to the ground state (or any other lower energy state). The uncertainty in energy of the excited state, due to its propensity to decay, gives rise to a slight smearing (in wavelength) of the spectral line associated with the transition. Strong lines, which correspond to fast transitions, are smeared out more that weak lines. For this reason, spectroscopists generally favor forbidden lines (see Section 8.10) for Doppler-shift measurements. Such lines are not as bright as those corresponding to allowed transitions, but they are a lot sharper.
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


