8.P: Exercises

1. Demonstrate that ${\bf p}\cdot{\bf A}={\bf A}\cdot{\bf p}$ when $\nabla\cdot{\bf A} = 0$ , where ${\bf p}$ is the momentum operator, and ${\bf A}({\bf x})$ is a real function of the position operator, ${\bf x}$ . Hence, show that the Hamiltonian $\ref{870}$ is Hermitian.
2. Find the selection rules for the matrix elements $\langle n,l,m\vert\,x\,\vert n',l',m'\rangle$ , $\langle n,l,m\vert\,y\,\vert n',l',m'\rangle$ , and $\langle n,l, m\vert\,z\,\vert n',l',m'\rangle$ to be non-zero. Here, $\vert n,l,m\rangle$ denotes an energy eigenket of a hydrogen-like atom corresponding to the conventional quantum numbers, $n$ , $l$ , and $m$ .
3. Demonstrate that \( \left\langle \vert\mbox{\boldmath\) where the average is taken over all directions of the incident radiation.
4. Demonstrate that the spontaneous decay rate (via an electric dipole transition) from any 2p state to a 1s state of a hydrogen atom is 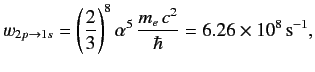where $\alpha$ is the fine structure constant. Hence, deduce that the natural line width of the associated spectral line is 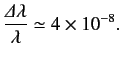The only non-zero $1s\leftrightarrow 2p$ electric dipole matrix elements take the values
$\langle 1,0,0\vert\,x\,\vert 2,1,\pm 1\rangle$ $= \pm\frac{2^7}{3^5}\,a_0,$ $\langle 1,0,0\vert\,y\,\vert 2,1,\pm 1\rangle$ $= {\rm i}\,\frac{2^7}{3^5}\,a_0,$ $\langle 1,0,0\vert\,z\,\vert 2,1,0\rangle$ $= \sqrt{2}\,\frac{2^7}{3^5}\,a_0,$ where $a_0$ is the Bohr radius.

Contributors

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  $\newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$