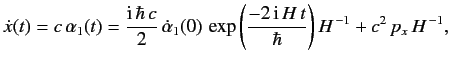11.4: Free Electron Motion

According to Equation $\ref{1129}$, the relativistic Hamiltonian of a free electron takes the form

\( \mbox{\boldmath\)$t$ that should be appended to dynamical variables that vary in time, according to the formalism of Section 3.2.

The above Hamiltonian is independent of ${\bf x}$ . Hence, momentum $x$ component of the velocity is

$j_x = \psi^\dag c\,\alpha_1\,\psi$ for the $\dot{x}$ , specified in the above equation, has the eigenvalues $\pm 1$ of $\dot{y}$ and $\dot{x}$ , we conclude that a measurement of a velocity component of a free electron is certain to yield the result $\pm c$ in a relativistic theory, consider the following argument. To measure the velocity we must measure the position at two slightly different times, and then divide the change in position by the time interval. (We cannot just measure the momentum and then apply a formula, because the ordinary connection between velocity and momentum is no longer valid.) In order that our measured velocity may approximate to the instantaneous velocity, the time interval between the two measurements of position must be very short, and the measurements themselves very accurate. However, the great accuracy with which the position of the electron is known during the time interval leads to an almost complete indeterminacy in its momentum, according to the Heisenberg uncertainty principle. This means that almost all values of the momentum are equally likely, so that the momentum is almost certain to be infinite. But, an infinite value of a momentum component corresponds to the values ${\rm i}\,\hbar\,\dot{\alpha}_1 =\alpha_1\,H-H\,\alpha_1.$ $\ref{1178}$

Now $H$ except $\alpha_1\,H+H\,\alpha_1 = \alpha_1\,c\,\alpha_1\,p^1 + c\,\alpha_1\,p^1\,\alpha_1 = 2\,c\,p^1.$

$\ref{1179}$

Here, use has been made of the fact that $p^1$ , and also that ${\rm i}\,\hbar\,\dot{\alpha}_1 = 2\,\alpha_1\,H-2\,c\,p^1.$ $\ref{1180}$

Since $H$ and ${\rm i}\,\hbar\,\ddot{\alpha}_1 = 2\,\dot{\alpha}_1\,H,$ $\ref{1181}$

which can be integrated to give

$\dot{\alpha}_1(t) = \dot{\alpha}_1\ref{0}\,\exp\left(\frac{-2\,{\rm i}\,H\,t}{\hbar}\right).$ $\ref{1182}$

It follows from Equation $\ref{1177}$ and $\ref{1180}$ that

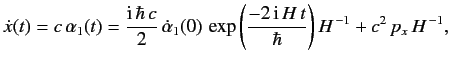$\ref{1183}$

and

$x$ -component of velocity consists of two parts, a constant part, $2\,H/h$ , is high (being at least $h/2\,m_e\,c^2$ ). The oscillatory part ensures that the instantaneous value of $\pm c$ . Note, finally, that the oscillatory part of $\hbar/m_e\,c$ .

Contributors

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  $\newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$