Skip to main content
\(\require{cancel}\)
Physics LibreTexts

11.P: Exercises

  1. Last updated
    08:45, 16 Nov 2014
  2. Save as PDF
  1. Noting that $ \alpha_i=-\beta\,\alpha_i\,\beta$ , prove that the $ \alpha_i$ and $ \beta$ matrices all have zero trace. Hence, deduce that each of these matrices has $ n$ eigenvalues $ +1$ , and $ n$ eigenvalues $ -1$ , where $ 2\,n$ is the dimension of the matrices.
  2. Verify that the matrices (1125) and (1126) satisfy Equations (1117)-(1119).
  3. Verify that the matrices (1123) and (1124) satisfy the anti-commutation relations (1122).
  4. Verify that if

     

    $\displaystyle \partial_\mu\,j^{\,\mu} = 0,$

     

    where $ j^{\,\mu}$ is a 4-vector field, then

     

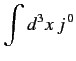    $\displaystyle \int d^3 x\,j^{\,0} $

     

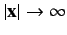    is Lorentz invariant, where the integral is over all space, and it is assumed that $ j^{\,\mu}\rightarrow 0$ as $ \vert{\bf x}\vert\rightarrow \infty$ .
  5. Verify that (1168) is a solution of (1167).
  6. Verify that the $ 4\times 4$ matrices $ \Sigma_i$ , defined in (1189), satisfy the standard anti-commutation relations for Pauli matrices: i.e.,

     

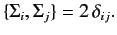
    $\displaystyle \{\Sigma_i, \Sigma_j\} = 2\,\delta_{ij}. $

Contributors