3.11: Practice

Conceptual Questions

Electric Charge

1. There are very large numbers of charged particles in most objects. Why, then, don’t most objects exhibit static electricity?

2. Why do most objects tend to contain nearly equal numbers of positive and negative charges?

3. A positively charged rod attracts a small piece of cork.

(a) Can we conclude that the cork is negatively charged?

(b) The rod repels another small piece of cork. Can we conclude that this piece is positively charged?

4. Two bodies attract each other electrically. Do they both have to be charged? Answer the same question if the bodies repel one another.

5. How would you determine whether the charge on a particular rod is positive or negative?

Conductors, Insulators, and Charging by Induction

6. An eccentric inventor attempts to levitate a cork ball by wrapping it with foil and placing a large negative charge on the ball and then putting a large positive charge on the ceiling of his workshop. Instead, while attempting to place a large negative charge on the ball, the foil flies off. Explain.

7. When a glass rod is rubbed with silk, it becomes positive and the silk becomes negative—yet both attract dust. Does the dust have a third type of charge that is attracted to both positive and negative? Explain.

8. Why does a car always attract dust right after it is polished? (Note that car wax and car tires are insulators.)

9. Does the uncharged conductor shown below experience a net electric force?

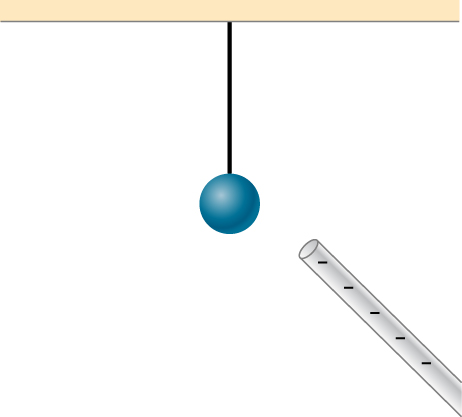
10. While walking on a rug, a person frequently becomes charged because of the rubbing between his shoes and the rug. This charge then causes a spark and a slight shock when the person gets close to a metal object. Why are these shocks so much more common on a dry day?

11. Compare charging by conduction to charging by induction.

12. Small pieces of tissue are attracted to a charged comb. Soon after sticking to the comb, the pieces of tissue are repelled from it. Explain.

13. Trucks that carry gasoline often have chains dangling from their undercarriages and brushing the ground. Why?

14. Why do electrostatic experiments work so poorly in humid weather?

15. Why do some clothes cling together after being removed from the clothes dryer? Does this happen if they’re still damp?

16. Can induction be used to produce charge on an insulator?

17. Suppose someone tells you that rubbing quartz with cotton cloth produces a third kind of charge on the quartz. Describe what you might do to test this claim.

18. A handheld copper rod does not acquire a charge when you rub it with a cloth. Explain why.

19. Suppose you place a charge q near a large metal plate.

(a) If q is attracted to the plate, is the plate necessarily charged?

(b) If q is repelled by the plate, is the plate necessarily charged?

Coulomb's Law

20. Would defining the charge on an electron to be positive have any effect on Coulomb’s law?

21. An atomic nucleus contains positively charged protons and uncharged neutrons. Since nuclei do stay together, what must we conclude about the forces between these nuclear particles?

22. Is the force between two fixed charges influenced by the presence of other charges?

Electric Field

23. When measuring an electric field, could we use a negative rather than a positive test charge?

24. During fair weather, the electric field due to the net charge on Earth points downward. Is Earth charged positively or negatively?

25. If the electric field at a point on the line between two charges is zero, what do you know about the charges?

26. Two charges lie along the x-axis. Is it true that the net electric field always vanishes at some point (other than infinity) along the x-axis?

Calculating Electric Fields of Charge Distributions

27. Give a plausible argument as to why the electric field outside an infinite charged sheet is constant.

28. Compare the electric fields of an infinite sheet of charge, an infinite, charged conducting plate, and infinite, oppositely charged parallel plates.

29. Describe the electric fields of an infinite charged plate and of two infinite, charged parallel plates in terms of the electric field of an infinite sheet of charge.

30. A negative charge is placed at the center of a ring of uniform positive charge. What is the motion (if any) of the charge? What if the charge were placed at a point on the axis of the ring other than the center?

Electric Field Lines

31. If a point charge is released from rest in a uniform electric field, will it follow a field line? Will it do so if the electric field is not uniform?

32. Under what conditions, if any, will the trajectory of a charged particle not follow a field line?

33. How would you experimentally distinguish an electric field from a gravitational field?

34. A representation of an electric field shows 10 field lines perpendicular to a square plate. How many field lines should pass perpendicularly through the plate to depict a field with twice the magnitude?

35. What is the ratio of the number of electric field lines leaving a charge 10q and a charge q?

Electric Dipoles

36. What are the stable orientation(s) for a dipole in an external electric field? What happens if the dipole is slightly perturbed from these orientations?

Electric Flux

1. Discuss how would orient a planar surface of area A in a uniform electric field of magnitude \(\displaystyle E_0\) to obtain

(a) the maximum flux and

(b) the minimum flux through the area.

2. What are the maximum and minimum values of the flux in the preceding question?

3. The net electric flux crossing a closed surface is always zero. True or false?

4. The net electric flux crossing an open surface is never zero. True or false?

Explaining Gauss’s Law

5. Two concentric spherical surfaces enclose a point charge q. The radius of the outer sphere is twice that of the inner one. Compare the electric fluxes crossing the two surfaces.

6. Compare the electric flux through the surface of a cube of side length a that has a charge q at its center to the flux through a spherical surface of radius a with a charge q at its center.

7. (a) If the electric flux through a closed surface is zero, is the electric field necessarily zero at all points on the surface?

(b) What is the net charge inside the surface?

8. Discuss how Gauss’s law would be affected if the electric field of a point charge did not vary as \(\displaystyle 1/r^2\).

9. Discuss the similarities and differences between the gravitational field of a point mass m and the electric field of a point charge q.

10. Discuss whether Gauss’s law can be applied to other forces, and if so, which ones.

11. Is the term \(\displaystyle \vec{E}\) in Gauss’s law the electric field produced by just the charge inside the Gaussian surface?

12. Reformulate Gauss’s law by choosing the unit normal of the Gaussian surface to be the one directed inward.

Applying Gauss’s Law

13. Would Gauss’s law be helpful for determining the electric field of two equal but opposite charges a fixed distance apart?

14. Discuss the role that symmetry plays in the application of Gauss’s law. Give examples of continuous charge distributions in which Gauss’s law is useful and not useful in determining the electric field.

15. Discuss the restrictions on the Gaussian surface used to discuss planar symmetry. For example, is its length important? Does the cross-section have to be square? Must the end faces be on opposite sides of the sheet?

Conductors in Electrostatic Equilibrium

16. Is the electric field inside a metal always zero?

17. Under electrostatic conditions, the excess charge on a conductor resides on its surface. Does this mean that all the conduction electrons in a conductor are on the surface?

18. A charge q is placed in the cavity of a conductor as shown below. Will a charge outside the conductor experience an electric field due to the presence of q?

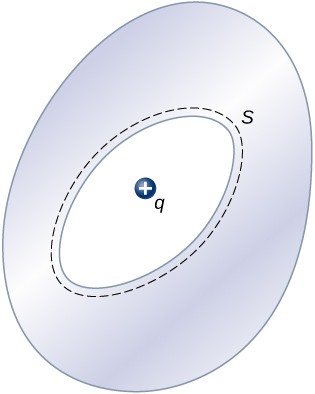
19. The conductor in the preceding figure has an excess charge of \(\displaystyle –5.0µC\). If a \(\displaystyle 2.0-µC\) point charge is placed in the cavity, what is the net charge on the surface of the cavity and on the outer surface of the conductor?

Problems

Electric Charge

37. Common static electricity involves charges ranging from nanocoulombs to microcoulombs.

(a) How many electrons are needed to form a charge of −2.00 nC?

(b) How many electrons must be removed from a neutral object to leave a net charge of 0.500μC?

38. If \(\displaystyle 1.80×10^{20}\) electrons move through a pocket calculator during a full day’s operation, how many coulombs of charge moved through it?

39. To start a car engine, the car battery moves \(\displaystyle 3.75×10^{21}\) electrons through the starter motor. How many coulombs of charge were moved?

40. A certain lightning bolt moves 40.0 C of charge. How many fundamental units of charge is this?

41. A 2.5-g copper penny is given a charge of \(\displaystyle −2.0×10^{−9}C\).

(a) How many excess electrons are on the penny?

(b) By what percent do the excess electrons change the mass of the penny?

42. A 2.5-g copper penny is given a charge of \(\displaystyle 4.0×10^{−9}C\).

(a) How many electrons are removed from the penny?

(b) If no more than one electron is removed from an atom, what percent of the atoms are ionized by this charging process?

Conductors, Insulators, and Charging by Induction

43. Suppose a speck of dust in an electrostatic precipitator has \(\displaystyle 1.0000×10^{12}\) protons in it and has a net charge of −5.00 nC (a very large charge for a small speck). How many electrons does it have?

44. An amoeba has \(\displaystyle 1.00×10^{16}\) protons and a net charge of 0.300 pC.

(a) How many fewer electrons are there than protons?

(b) If you paired them up, what fraction of the protons would have no electrons?

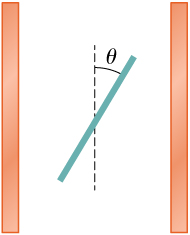
45. A 50.0-g ball of copper has a net charge of 2.00μC. What fraction of the copper’s electrons has been removed? (Each copper atom has 29 protons, and copper has an atomic mass of 63.5.)

46. What net charge would you place on a 100-g piece of sulfur if you put an extra electron on 1 in \(\displaystyle 10^{12}\) of its atoms? (Sulfur has an atomic mass of 32.1 u.)

47. How many coulombs of positive charge are there in 4.00 kg of plutonium, given its atomic mass is 244 and that each plutonium atom has 94 protons?

Coulomb's Law

48. Two point particles with charges +3μC and +5μC are held in place by 3-N forces on each charge in appropriate directions. (a) Draw a free-body diagram for each particle. (b) Find the distance between the charges.

49. Two charges +3μC and +12μC are fixed 1 m apart, with the second one to the right. Find the magnitude and direction of the net force on a −2-nC charge when placed at the following locations:

(a) halfway between the two

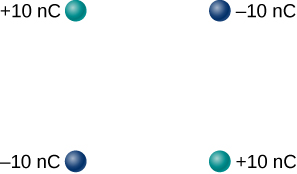
(b) half a meter to the left of the +3μC charge

(c) half a meter above the +12μC charge in a direction perpendicular to the line joining the two fixed charges

50. In a salt crystal, the distance between adjacent sodium and chloride ions is \(\displaystyle 2.82×10^{−10}m\). What is the force of attraction between the two singly charged ions?

51. Protons in an atomic nucleus are typically \(\displaystyle 10^{−15}m\) apart. What is the electric force of repulsion between nuclear protons?

52. Suppose Earth and the Moon each carried a net negative charge −Q. Approximate both bodies as point masses and point charges.

(a) What value of Q is required to balance the gravitational attraction between Earth and the Moon?

(b) Does the distance between Earth and the Moon affect your answer? Explain.

(c) How many electrons would be needed to produce this charge?

53. Point charges \(\displaystyle q_1=50μC\) and \(\displaystyle q_2=−25μC\) are placed 1.0 m apart. What is the force on a third charge \(\displaystyle q_3=20μC\) placed midway between \(\displaystyle q_1\) and \(\displaystyle q_2\)?

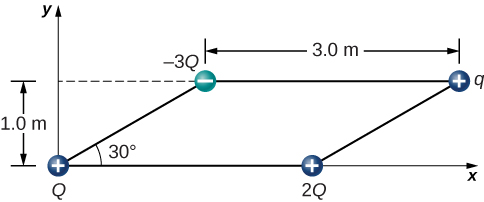
54. Where must \(\displaystyle q_3\) of the preceding problem be placed so that the net force on it is zero?

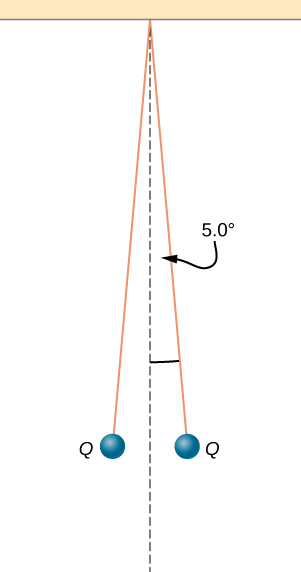
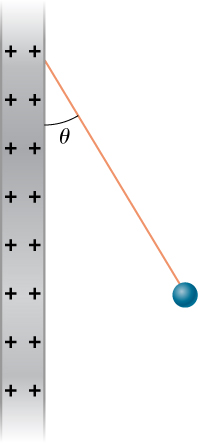
55. Two small balls, each of mass 5.0 g, are attached to silk threads 50 cm long, which are in turn tied to the same point on the ceiling, as shown below. When the balls are given the same charge Q, the threads hang at 5.0° to the vertical, as shown below. What is the magnitude of Q? What are the signs of the two charges?

56. Point charges \(\displaystyle Q_1=2.0μC\) and \(\displaystyle Q_2=4.0μC\) are located at \(\displaystyle \vec{r_1}=(4.0\hat{i}−2.0\hat{j}+5.0\hat{k})m\) and \(\displaystyle \vec{r_2}=(8.0\hat{i}+5.0\hat{j}−9.0\hat{k})m\). What is the force of \(\displaystyle Q_2\) on \(\displaystyle Q_1\)?

57. The net excess charge on two small spheres (small enough to be treated as point charges) is Q. Show that the force of repulsion between the spheres is greatest when each sphere has an excess charge Q/2. Assume that the distance between the spheres is so large compared with their radii that the spheres can be treated as point charges.

58. Two small, identical conducting spheres repel each other with a force of 0.050 N when they are 0.25 m apart. After a conducting wire is connected between the spheres and then removed, they repel each other with a force of 0.060 N. What is the original charge on each sphere?

59. A charge q=2.0μC is placed at the point P shown below. What is the force on q?

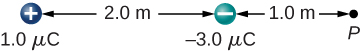
60. What is the net electric force on the charge located at the lower right-hand corner of the triangle shown here?

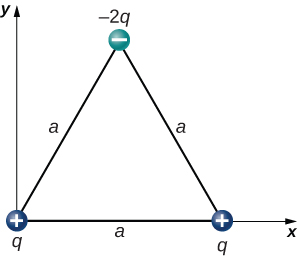
61. Two fixed particles, each of charge \(\displaystyle 5.0×10^{−6}C\), are 24 cm apart. What force do they exert on a third particle of charge \(\displaystyle −2.5×10^{−6}C\) that is 13 cm from each of them?

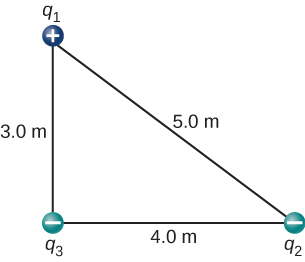
62. The charges \(\displaystyle q_1=2.0×10^{−7}C,q_2=−4.0×10^{−7}C\), and \(\displaystyle q_3=−1.0×10^{−7}C\) are placed at the corners of the triangle shown below. What is the force on \(\displaystyle q_1\)?

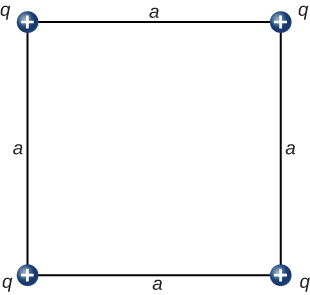
63. What is the force on the charge q at the lower-right-hand corner of the square shown here?

64. Point charges \(\displaystyle q_1=10μC\) and \(\displaystyle q_2=−30μC\) are fixed at \(\displaystyle r_1=(3.0\hat{i}−4.0\hat{j})m\) and \(\displaystyle r_2=(9.0\hat{i}+6.0\hat{j})m.\) What is the force of \(\displaystyle q_2\) on \(\displaystyle q_1\)?

Electric Field

65. A particle of charge \(\displaystyle 2.0×10^{−8}C\) experiences an upward force of magnitude \(\displaystyle 4.0×10^{−6}N\) when it is placed in a particular point in an electric field.

(a) What is the electric field at that point?

(b) If a charge \(\displaystyle q=−1.0×10^{−8}C\) is placed there, what is the force on it?

66. On a typical clear day, the atmospheric electric field points downward and has a magnitude of approximately 100 N/C. Compare the gravitational and electric forces on a small dust particle of mass \(\displaystyle 2.0×10^{−15}g\) that carries a single electron charge. What is the acceleration (both magnitude and direction) of the dust particle?

67. Consider an electron that is 10−10m10−10m from an alpha particle (q=3.2×10−19C).(q=3.2×10−19C).

(a) What is the electric field due to the alpha particle at the location of the electron?

(b) What is the electric field due to the electron at the location of the alpha particle?

(c) What is the electric force on the alpha particle? On the electron?

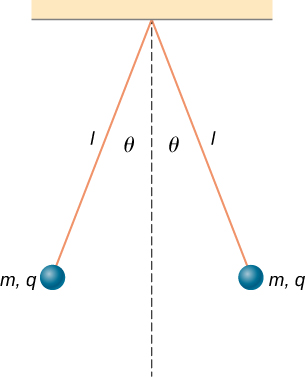
68. Each the balls shown below carries a charge q and has a mass m. The length of each thread is l, and at equilibrium, the balls are separated by an angle \(\displaystyle 2θ\). How does \(\displaystyle θ\) vary with q and l? Show that \(\displaystyle θ\) satisfies \(\displaystyle sin(θ)^2tan(θ)=\frac{q^2}{16πε0gl^2m\).

69. What is the electric field at a point where the force on a \(\displaystyle −2.0×10^{−6}−C\) charge is \(\displaystyle (4.0\hat{i}−6.0\hat{j})×10^{−6}N\)?

70. A proton is suspended in the air by an electric field at the surface of Earth. What is the strength of this electric field?

71. The electric field in a particular thundercloud is \(\displaystyle 2.0×10^5N/C\). What is the acceleration of an electron in this field?

72. A small piece of cork whose mass is 2.0 g is given a charge of \(\displaystyle 5.0×10^{−7}C\). What electric field is needed to place the cork in equilibrium under the combined electric and gravitational forces?

73. If the electric field is 100N/C at a distance of 50 cm from a point charge q, what is the value of q?

74. What is the electric field of a proton at the first Bohr orbit for hydrogen \(\displaystyle (r=5.29×10^{−11}m)\)? What is the force on the electron in that orbit?

75. (a) What is the electric field of an oxygen nucleus at a point that is \(\displaystyle 10^{−10}m\) from the nucleus?

(b) What is the force this electric field exerts on a second oxygen nucleus placed at that point?

76. Two point charges, \(\displaystyle q_1=2.0×10^{−7}C\) and \(\displaystyle q_2=−6.0×10^{−8}C\), are held 25.0 cm apart.

(a) What is the electric field at a point 5.0 cm from the negative charge and along the line between the two charges?

(b)What is the force on an electron placed at that point?

77. Point charges \(\displaystyle q_1=50μC\) and \(\displaystyle q_2=−25μC\) are placed 1.0 m apart.

(a) What is the electric field at a point midway between them?

(b) What is the force on a charge \(\displaystyle q_3=20μC\) situated there?

78. Can you arrange the two point charges \(\displaystyle q_1=−2.0×10^{−6}C\) and \(\displaystyle q_2=4.0×10^{−6}C\) along the x-axis so that \(\displaystyle E=0\) at the origin?

79. Point charges \(\displaystyle q_1=q_2=4.0×10^{−6}C\) are fixed on the x-axis at \(\displaystyle x=−3.0m\) and \(\displaystyle x=3.0m\). What charge q must be placed at the origin so that the electric field vanishes at x=0,y=3.0m?

Calculating Electric Fields of Charge Distributions

80. A thin conducting plate 1.0 m on the side is given a charge of \(\displaystyle −2.0×10^{−6}C\). An electron is placed 1.0 cm above the center of the plate. What is the acceleration of the electron?

81. Calculate the magnitude and direction of the electric field 2.0 m from a long wire that is charged uniformly at \(\displaystyle λ=4.0×10^{−6}C/m\).

82. Two thin conducting plates, each 25.0 cm on a side, are situated parallel to one another and 5.0 mm apart. If \(\displaystyle 10^{11}\) electrons are moved from one plate to the other, what is the electric field between the plates?

83. The charge per unit length on the thin rod shown below is \(\displaystyle λ\). What is the electric field at the point P? (Hint: Solve this problem by first considering the electric field \(\displaystyle d\vec{E}\) at P due to a small segment dx of the rod, which contains charge \(\displaystyle dq=λdx\). Then find the net field by integrating \(\displaystyle d\vec{E}\) over the length of the rod.)

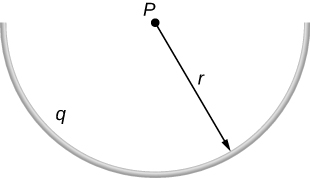
84. The charge per unit length on the thin semicircular wire shown below is λ. What is the electric field at the point P?

85. Two thin parallel conducting plates are placed 2.0 cm apart. Each plate is 2.0 cm on a side; one plate carries a net charge of 8.0μC, and the other plate carries a net charge of −8.0μC. What is the charge density on the inside surface of each plate? What is the electric field between the plates?

86. A thin conducting plate 2.0 m on a side is given a total charge of −10.0μC.

(a) What is the electric field 1.0cm above the plate?

(b) What is the force on an electron at this point?

(c) Repeat these calculations for a point 2.0 cm above the plate.

(d) When the electron moves from 1.0 to 2,0 cm above the plate, how much work is done on it by the electric field?

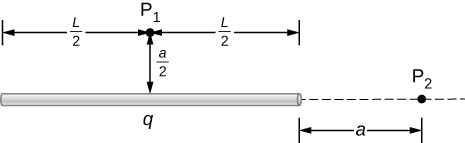
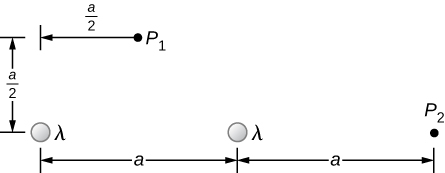
87. A total charge q is distributed uniformly along a thin, straight rod of length L (see below). What is the electric field at \(\displaystyle P_1\)? At \(\displaystyle P_2\)?

88. Charge is distributed along the entire x-axis with uniform density λ. How much work does the electric field of this charge distribution do on an electron that moves along the y-axis from \(\displaystyle y=a\) to \(\displaystyle y=b\)?

89. Charge is distributed along the entire x-axis with uniform density \(\displaystyle λ_x\) and along the entire y-axis with uniform density \(\displaystyle λ_y\). Calculate the resulting electric field at

(a) \(\displaystyle \vec{r} = a\hat{i}+b\hat{j}\) and

(b) \(\displaystyle \vec{r} =c\hat{k}\).

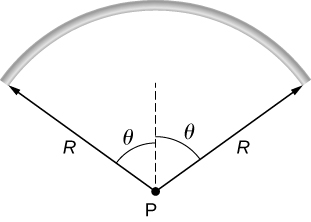
90. A rod bent into the arc of a circle subtends an angle \(\displaystyle 2θ\) at the center P of the circle (see below). If the rod is charged uniformly with a total charge Q, what is the electric field at P?.

91. A proton moves in the electric field \(\displaystyle \vec{E} = 200\hat{i}N/C\). (a) What are the force on and the acceleration of the proton? (b) Do the same calculation for an electron moving in this field.

92. An electron and a proton, each starting from rest, are accelerated by the same uniform electric field of 200 N/C. Determine the distance and time for each particle to acquire a kinetic energy of \(\displaystyle 3.2×10^{−16}J\).

93. A spherical water droplet of radius 25μm carries an excess 250 electrons. What vertical electric field is needed to balance the gravitational force on the droplet at the surface of the earth?

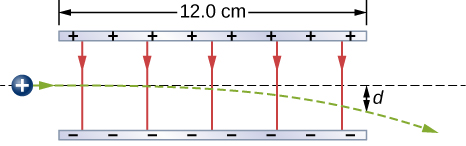
94. A proton enters the uniform electric field produced by the two charged plates shown below. The magnitude of the electric field is \(\displaystyle 4.0×10^5N/C\), and the speed of the proton when it enters is \(\displaystyle 1.5×10^7m/s\). What distance d has the proton been deflected downward when it leaves the plates?

95. Shown below is a small sphere of mass 0.25 g that carries a charge of \(\displaystyle 9.0×10^{−10}C\). The sphere is attached to one end of a very thin silk string 5.0 cm long. The other end of the string is attached to a large vertical conducting plate that has a charge density of \(\displaystyle 30×10^{−6}C/m^2\). What is the angle that the string makes with the vertical?

96. Two infinite rods, each carrying a uniform charge density \(\displaystyle λ\), are parallel to one another and perpendicular to the plane of the page. (See below.) What is the electrical field at \(\displaystyle P_1\)? At \(\displaystyle P_2\)?

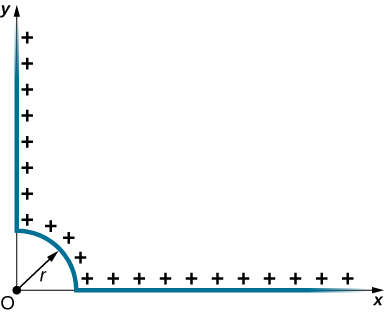
97. Positive charge is distributed with a uniform density \(\displaystyle λ\) along the positive x-axis from \(\displaystyle r\) to \(\displaystyle ∞\), along the positive y-axis from \(\displaystyle r\) to \(\displaystyle ∞\), and along a 90° arc of a circle of radius r, as shown below. What is the electric field at O?

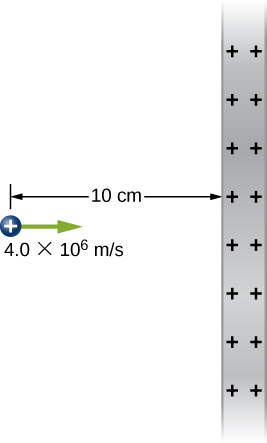
98. From a distance of 10 cm, a proton is projected with a speed of \(\displaystyle v=4.0×10^6m/s\) directly at a large, positively charged plate whose charge density is \(\displaystyle σ=2.0×10^{−5}C/m^2\).. (See below.)

(a) Does the proton reach the plate?

(b) If not, how far from the plate does it turn around?

99. A particle of mass m and charge \(\displaystyle −q\) moves along a straight line away from a fixed particle of charge Q. When the distance between the two particles is \(\displaystyle r_0,−q\) is moving with a speed \(\displaystyle v_0\).

(a) Use the work-energy theorem to calculate the maximum separation of the charges.

(b) What do you have to assume about \(\displaystyle v_0\) to make this calculation?

(c) What is the minimum value of \(\displaystyle v_0\) such that \(\displaystyle −q\) escapes from Q?

Electric Field Lines

100. Which of the following electric field lines are incorrect for point charges? Explain why.

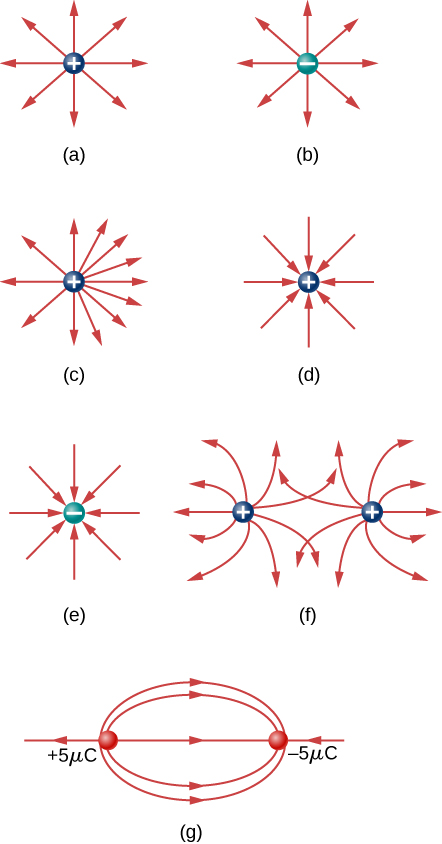
101. In this exercise, you will practice drawing electric field lines. Make sure you represent both the magnitude and direction of the electric field adequately. Note that the number of lines into or out of charges is proportional to the charges.

(a) Draw the electric field lines map for two charges +20μC and −20μC situated 5 cm from each other.

(b) Draw the electric field lines map for two charges +20μC and +20μC situated 5 cm from each other.

(c) Draw the electric field lines map for two charges +20μC and −30μC situated 5 cm from each other.

102. Draw the electric field for a system of three particles of charges +1μC, +2μC and −3μC fixed at the corners of an equilateral triangle of side 2 cm.

103. Two charges of equal magnitude but opposite sign make up an electric dipole. A quadrupole consists of two electric dipoles that are placed anti-parallel at two edges of a square as shown. Draw the electric field of the charge distribution.

104. Suppose the electric field of an isolated point charge decreased with distance as \(\displaystyle 1/r^{2+δ}\) rather than as \(\displaystyle 1/r^2\). Show that it is then impossible to draw continuous field lines so that their number per unit area is proportional to E.

Electric Dipoles

105. Consider the equal and opposite charges shown below. (a) Show that at all points on the x-axis for which \(\displaystyle |x|≫a,E≈Qa/2πε_0x^3\). (b) Show that at all points on the y-axis for which \(\displaystyle |y|≫a,E≈Qa/πε_0y^3\).

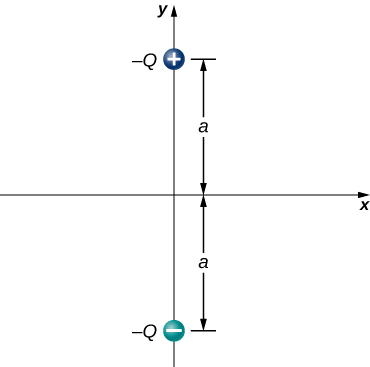
106. (a) What is the dipole moment of the configuration shown above? If Q=4.0μC,

(b) what is the torque on this dipole with an electric field of \(\displaystyle 4.0×10^5N/C\hat{i}\)?

(c) What is the torque on this dipole with an electric field of \(\displaystyle −4.0×10^5N/C\hat{i}\)?

(d) What is the torque on this dipole with an electric field of \(\displaystyle ±4.0×10^5N/C\hat{j}\)?

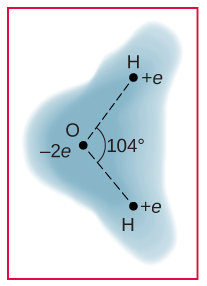
107. A water molecule consists of two hydrogen atoms bonded with one oxygen atom. The bond angle between the two hydrogen atoms is 104° (see below). Calculate the net dipole moment of a hypothetical water molecule where the charge at the oxygen molecule is −2e and at each hydrogen atom is +e. The net dipole moment of the molecule is the vector sum of the individual dipole moment between the two O-Hs. The separation O-H is 0.9578 angstroms.

Problems

Electric Flux

20. A uniform electric field of magnitude \(\displaystyle 1.1×10^4N/C\) is perpendicular to a square sheet with sides 2.0 m long. What is the electric flux through the sheet?

21. Calculate the flux through the sheet of the previous problem if the plane of the sheet is at an angle of 60° to the field. Find the flux for both directions of the unit normal to the sheet.

22. Find the electric flux through a rectangular area 3cm×2cm between two parallel plates where there is a constant electric field of 30 N/C for the following orientations of the area: (a) parallel to the plates, (b) perpendicular to the plates, and (c) the normal to the area making a 30° angle with the direction of the electric field. Note that this angle can also be given as 180°+30°.

23. The electric flux through a square-shaped area of side 5 cm near a large charged sheet is found to be \(\displaystyle 3×10^{−5}N⋅m^2/C\). when the area is parallel to the plate. Find the charge density on the sheet.

24. Two large rectangular aluminum plates of area \(\displaystyle 150cm^2\) face each other with a separation of 3 mm between them. The plates are charged with equal amount of opposite charges, ±20μC. The charges on the plates face each other. Find the flux through a circle of radius 3 cm between the plates when the normal to the circle makes an angle of 5° with a line perpendicular to the plates. Note that this angle can also be given as 180°+5°.

25. A square surface of area \(\displaystyle 2cm^2\) is in a space of uniform electric field of magnitude \(\displaystyle 10^3N/C\). The amount of flux through it depends on how the square is oriented relative to the direction of the electric field. Find the electric flux through the square, when the normal to it makes the following angles with electric field: (a) 30°, (b) 90°, and (c) 0°. Note that these angles can also be given as 180°+θ.

26. A vector field is pointed along the z-axis, \(\displaystyle \vec{v} =\frac{α}{x^2+y^2}\hat{z}.

(a) Find the flux of the vector field through a rectangle in the xy-plane between a<x<ba<x<b and c<y<dc<y<d.

(b) Do the same through a rectangle in the yz-plane between a<z<ba<z<b and c<y<dc<y<d. (Leave your answer as an integral.)

27. Consider the uniform electric field \(\displaystyle \vec{E} =(4.0\hat{j}+3.0\hat{k})×10^3N/C\). What is its electric flux through a circular area of radius 2.0 m that lies in the xy-plane?

28. Repeat the previous problem, given that the circular area is (a) in the yz-plane and (b) 45° above the xy-plane.

29. An infinite charged wire with charge per unit length \(\displaystyle λ\) lies along the central axis of a cylindrical surface of radius r and length l. What is the flux through the surface due to the electric field of the charged wire?

Explaining Gauss’s Law

30. Determine the electric flux through each closed surface whose cross-section inside the surface is shown below.

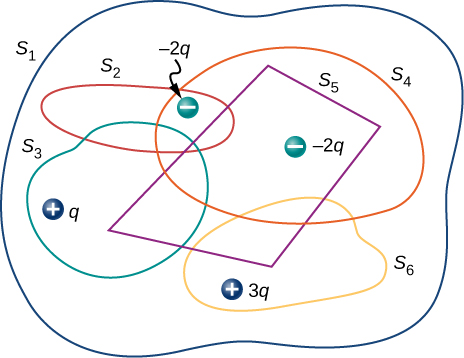
31. Find the electric flux through the closed surface whose cross-sections are shown below.

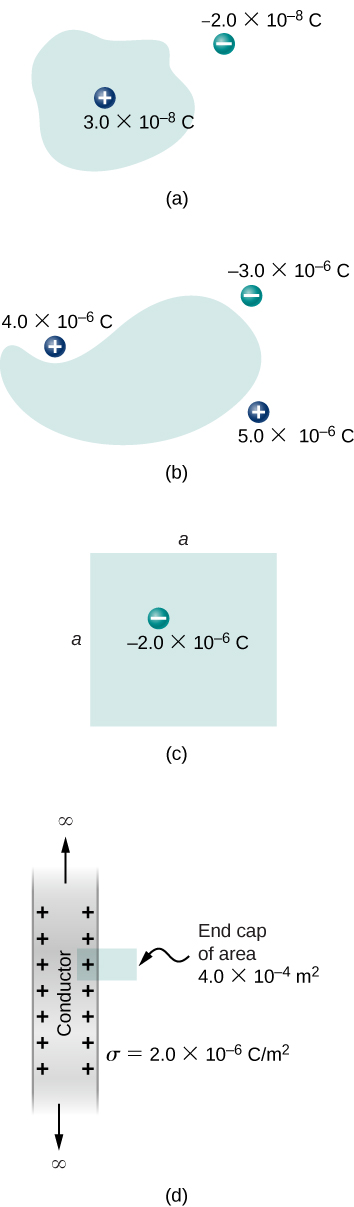
32. A point charge q is located at the center of a cube whose sides are of length a. If there are no other charges in this system, what is the electric flux through one face of the cube?

33. A point charge of \(\displaystyle 10μC\) is at an unspecified location inside a cube of side 2 cm. Find the net electric flux though the surfaces of the cube.

34. A net flux of \(\displaystyle 1.0×10^4N⋅^m2/C\) passes inward through the surface of a sphere of radius 5 cm.

(a) How much charge is inside the sphere?

(b) How precisely can we determine the location of the charge from this information?

35. A charge q is placed at one of the corners of a cube of side a, as shown below. Find the magnitude of the electric flux through the shaded face due to q. Assume \(\displaystyle q>0\).

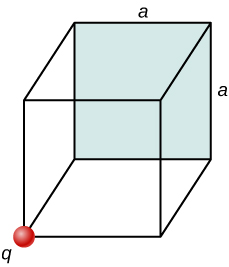
36. The electric flux through a cubical box 8.0 cm on a side is \(\displaystyle 1.2×10^3N⋅m^2/C\). What is the total charge enclosed by the box?

37. The electric flux through a spherical surface is \(\displaystyle 4.0×10^4N⋅m^2/C\). What is the net charge enclosed by the surface?

38. A cube whose sides are of length d is placed in a uniform electric field of magnitude \(\displaystyle E=4.0×10^3N/C\) so that the field is perpendicular to two opposite faces of the cube. What is the net flux through the cube?

39. Repeat the previous problem, assuming that the electric field is directed along a body diagonal of the cube.

40. A total charge \(\displaystyle 5.0×10^{−6}C\) is distributed uniformly throughout a cubical volume whose edges are 8.0 cm long.

(a) What is the charge density in the cube?

(b) What is the electric flux through a cube with 12.0-cm edges that is concentric with the charge distribution?

(c) Do the same calculation for cubes whose edges are 10.0 cm long and 5.0 cm long.

(d) What is the electric flux through a spherical surface of radius 3.0 cm that is also concentric with the charge distribution?

Applying Gauss’s Law

41. Recall that in the example of a uniform charged sphere, \(\displaystyle ρ_0=Q/(\frac{4}{3}πR^3)\). Rewrite the answers in terms of the total charge Q on the sphere.

42. Suppose that the charge density of the spherical charge distribution shown in Figure 6.23 is \(\displaystyle ρ(r)=ρ_0r/R\) for \(\displaystyle r≤R\) and zero for \(\displaystyle r>R\). Obtain expressions for the electric field both inside and outside the distribution.

43. A very long, thin wire has a uniform linear charge density of \(\displaystyle 50μC/m\). What is the electric field at a distance 2.0 cm from the wire?

44. A charge of \(\displaystyle −30μC\) is distributed uniformly throughout a spherical volume of radius 10.0 cm. Determine the electric field due to this charge at a distance of

(a) 2.0 cm,

(b) 5.0 cm, and

(c) 20.0 cm from the center of the sphere.

45. Repeat your calculations for the preceding problem, given that the charge is distributed uniformly over the surface of a spherical conductor of radius 10.0 cm.

46. A total charge Q is distributed uniformly throughout a spherical shell of inner and outer radii \(\displaystyle r_1\) and \(\displaystyle r_2\), respectively. Show that the electric field due to the charge is

\(\displaystyle \vec{E} =\vec{0}\) \(\displaystyle (r≤r_1)\);

\(\displaystyle \vec{E} =\frac{Q}{4πε_0r^2}(\frac{r^3−r_1^3}{r_2^3−r_1^3})\hat{r}\) \(\displaystyle (r_1≤r≤r_2)\);

\(\displaystyle \vec{E} =\frac{Q}{4πε_0r^2}\hat{r}\) \(\displaystyle (r≥r_2)\).

47. When a charge is placed on a metal sphere, it ends up in equilibrium at the outer surface. Use this information to determine the electric field of \(\displaystyle +3.0μC\) charge put on a 5.0-cm aluminum spherical ball at the following two points in space:

(a) a point 1.0 cm from the center of the ball (an inside point) and

(b) a point 10 cm from the center of the ball (an outside point).

48. A large sheet of charge has a uniform charge density of \(\displaystyle 10μC/m^2\). What is the electric field due to this charge at a point just above the surface of the sheet?

49. Determine if approximate cylindrical symmetry holds for the following situations. State why or why not.

(a) A 300-cm long copper rod of radius 1 cm is charged with +500 nC of charge and we seek electric field at a point 5 cm from the center of the rod.

(b) A 10-cm long copper rod of radius 1 cm is charged with +500 nC of charge and we seek electric field at a point 5 cm from the center of the rod.

(c) A 150-cm wooden rod is glued to a 150-cm plastic rod to make a 300-cm long rod, which is then painted with a charged paint so that one obtains a uniform charge density. The radius of each rod is 1 cm, and we seek an electric field at a point that is 4 cm from the center of the rod.

(d) Same rod as (c), but we seek electric field at a point that is 500 cm from the center of the rod.

50. A long silver rod of radius 3 cm has a charge of \(\displaystyle −5μC/cm\) on its surface.

(a) Find the electric field at a point 5 cm from the center of the rod (an outside point).

(b) Find the electric field at a point 2 cm from the center of the rod (an inside point).

51. The electric field at 2 cm from the center of long copper rod of radius 1 cm has a magnitude 3 N/C and directed outward from the axis of the rod.

(a) How much charge per unit length exists on the copper rod?

(b) What would be the electric flux through a cube of side 5 cm situated such that the rod passes through opposite sides of the cube perpendicularly?

52. A long copper cylindrical shell of inner radius 2 cm and outer radius 3 cm surrounds concentrically a charged long aluminum rod of radius 1 cm with a charge density of 4 pC/m. All charges on the aluminum rod reside at its surface. The inner surface of the copper shell has exactly opposite charge to that of the aluminum rod while the outer surface of the copper shell has the same charge as the aluminum rod. Find the magnitude and direction of the electric field at points that are at the following distances from the center of the aluminum rod:

(a) 0.5 cm, (b) 1.5 cm, (c) 2.5 cm, (d) 3.5 cm, and (e) 7 cm.

53. Charge is distributed uniformly with a density \(\displaystyle ρ\) throughout an infinitely long cylindrical volume of radius R. Show that the field of this charge distribution is directed radially with respect to the cylinder and that

\(\displaystyle E=\frac{ρr}{2ε_0}\) \(\displaystyle (r≤R)\);

\(\displaystyle E=\frac{ρR^2}{2ε_0r}\) \(\displaystyle (r≥R)\)

54. Charge is distributed throughout a very long cylindrical volume of radius R such that the charge density increases with the distance r from the central axis of the cylinder according to \(\displaystyle ρ=αr\), where \(\displaystyle α\) is a constant. Show that the field of this charge distribution is directed radially with respect to the cylinder and that

\(\displaystyle E=\frac{αr^2}{3ε_0}\) \(\displaystyle (r≤R)\);

\(\displaystyle E=\frac{αR^3}{3ε_0r}\) \(\displaystyle (r≥R)\).

55. The electric field 10.0 cm from the surface of a copper ball of radius 5.0 cm is directed toward the ball’s center and has magnitude \(\displaystyle 4.0×10^2N/C\). How much charge is on the surface of the ball?

56. Charge is distributed throughout a spherical shell of inner radius \(\displaystyle r_1\) and outer radius \(\displaystyle r_2\) with a volume density given by \(\displaystyle ρ=ρ_0r_1/r\), where \(\displaystyle ρ_0\) is a constant. Determine the electric field due to this charge as a function of r, the distance from the center of the shell.

57. Charge is distributed throughout a spherical volume of radius R with a density \(\displaystyle ρ=αr^2\), where αα is a constant. Determine the electric field due to the charge at points both inside and outside the sphere.

58. Consider a uranium nucleus to be sphere of radius \(\displaystyle R=7.4×10^{−15}m\) with a charge of 92e distributed uniformly throughout its volume. (a) What is the electric force exerted on an electron when it is \(\displaystyle 3.0×10^{−15}m\) from the center of the nucleus? (b) What is the acceleration of the electron at this point?

59. The volume charge density of a spherical charge distribution is given by \(\displaystyle ρ(r)=ρ_0e^{−αr}\), where \(\displaystyle ρ_0\) and \(\displaystyle α\) are constants. What is the electric field produced by this charge distribution?

Conductors in Electrostatic Equilibrium

60. An uncharged conductor with an internal cavity is shown in the following figure. Use the closed surface S along with Gauss’ law to show that when a charge q is placed in the cavity a total charge –q is induced on the inner surface of the conductor. What is the charge on the outer surface of the conductor?

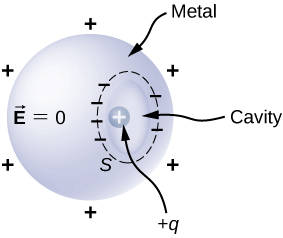
61. An uncharged spherical conductor S of radius R has two spherical cavities A and B of radii a and b, respectively as shown below. Two point charges \(\displaystyle +q_a\) and \(\displaystyle +q_b\) are placed at the center of the two cavities by using non-conducting supports. In addition, a point charge \(\displaystyle +q_0\) is placed outside at a distance r from the center of the sphere.

(a) Draw approximate charge distributions in the metal although metal sphere has no net charge.

(b) Draw electric field lines. Draw enough lines to represent all distinctly different places.

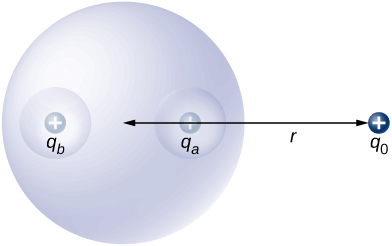
62. A positive point charge is placed at the angle bisector of two uncharged plane conductors that make an angle of 45°.See below. Draw the electric field lines.

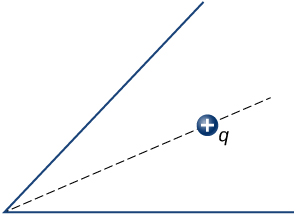
63. A long cylinder of copper of radius 3 cm is charged so that it has a uniform charge per unit length on its surface of 3 C/m. (a) Find the electric field inside and outside the cylinder. (b) Draw electric field lines in a plane perpendicular to the rod.

64. An aluminum spherical ball of radius 4 cm is charged with 5μC of charge. A copper spherical shell of inner radius 6 cm and outer radius 8 cm surrounds it. A total charge of −8μC is put on the copper shell.

(a) Find the electric field at all points in space, including points inside the aluminum and copper shell when copper shell and aluminum sphere are concentric.

(b) Find the electric field at all points in space, including points inside the aluminum and copper shell when the centers of copper shell and aluminum sphere are 1 cm apart.

65. A long cylinder of aluminum of radius R meters is charged so that it has a uniform charge per unit length on its surface of \(\displaystyle λ\). (a) Find the electric field inside and outside the cylinder. (b) Plot electric field as a function of distance from the center of the rod.

66. At the surface of any conductor in electrostatic equilibrium, \(\displaystyle E=σ/ε_0\). Show that this equation is consistent with the fact that \(\displaystyle E=kq/r^2\) at the surface of a spherical conductor.

67. Two parallel plates 10 cm on a side are given equal and opposite charges of magnitude \(\displaystyle 5.0×10^{−9}C\). The plates are 1.5 mm apart. What is the electric field at the center of the region between the plates?

68. Two parallel conducting plates, each of cross-sectional area \(\displaystyle 400cm^2\), are 2.0 cm apart and uncharged. If \(\displaystyle 1.0×10^{12}\) electrons are transferred from one plate to the other, what are (a) the charge density on each plate? (b) The electric field between the plates?

69. The surface charge density on a long straight metallic pipe is \(\displaystyle σ\). What is the electric field outside and inside the pipe? Assume the pipe has a diameter of 2a.

70. A point charge \(\displaystyle q=−5.0×10^{−12}C\) is placed at the center of a spherical conducting shell of inner radius 3.5 cm and outer radius 4.0 cm. The electric field just above the surface of the conductor is directed radially outward and has magnitude 8.0 N/C.

(a) What is the charge density on the inner surface of the shell?

(b) What is the charge density on the outer surface of the shell?

(c) What is the net charge on the conductor?

71. A solid cylindrical conductor of radius a is surrounded by a concentric cylindrical shell of inner radius b. The solid cylinder and the shell carry charges +Q and –Q, respectively. Assuming that the length L of both conductors is much greater than a or b, determine the electric field as a function of r, the distance from the common central axis of the cylinders, for (a) \(\displaystyle r<a\); (b) \(\displaystyle a<r<b\); and (c) \(\displaystyle r>b\).

Additional Problems

108. Point charges \(\displaystyle q_1=2.0μC\) and \(\displaystyle q_1=4.0μC\) are located at \(\displaystyle r_1=(4.0\hat{i}−2.0\hat{j}+2.0\hat{k})m\) and \(\displaystyle r_2=(8.0\hat{i}+5.0\hat{j}−9.0\hat{k})m\). What is the force of \(\displaystyle q_2\) on \(\displaystyle q_1\)?

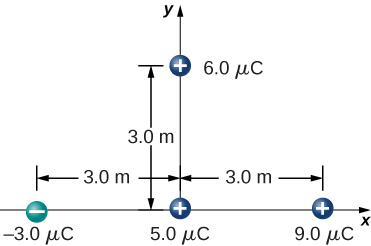
109. What is the force on the 5.0-μC charges shown below?

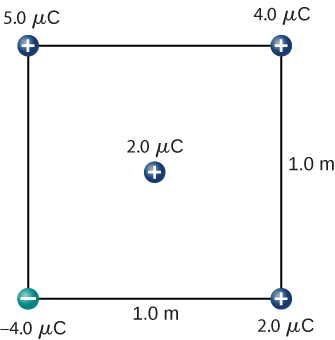
110. What is the force on the 2.0-μC charge placed at the center of the square shown below?

111. Four charged particles are positioned at the corners of a parallelogram as shown below. If \(\displaystyle q=5.0μC\) and \(\displaystyle Q=8.0μC\), what is the net force on q?

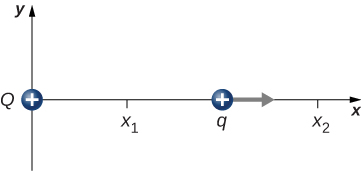
112. A charge Q is fixed at the origin and a second charge q moves along the x-axis, as shown below. How much work is done on q by the electric force when q moves from \(\displaystyle x_1\) to \(\displaystyle x_2\)?

113. A charge q=−2.0μC is released from rest when it is 2.0 m from a fixed charge \(\displaystyle Q=6.0μC\). What is the kinetic energy of q when it is 1.0 m from Q?

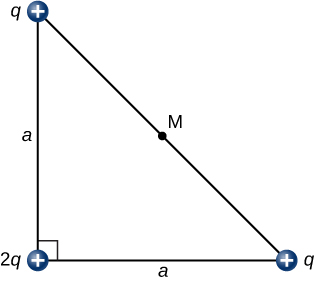
114. What is the electric field at the midpoint M of the hypotenuse of the triangle shown below?

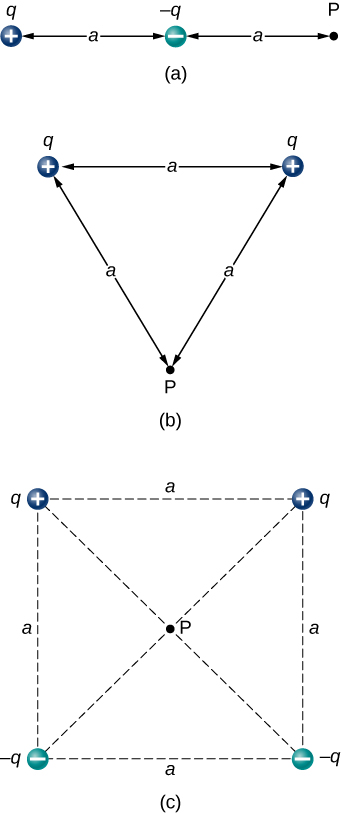
115. Find the electric field at P for the charge configurations shown below.

116. (a) What is the electric field at the lower-right-hand corner of the square shown below? (b) What is the force on a charge q placed at that point?

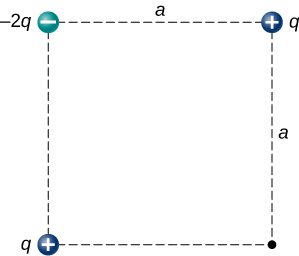
117. Point charges are placed at the four corners of a rectangle as shown below: \(\displaystyle q_1=2.0×10^{−6}C, q_2=−2.0×10^{−6}C, q_3=4.0×10^{−6}C,\) and \(\displaystyle q_4=1.0×10^{−6}C\). What is the electric field at P?

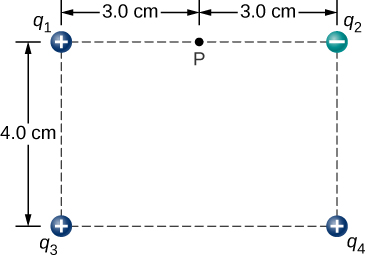
118. Three charges are positioned at the corners of a parallelogram as shown below. (a) If \(\displaystyle Q=8.0μC\), what is the electric field at the unoccupied corner? (b) What is the force on a 5.0-μC charge placed at this corner?

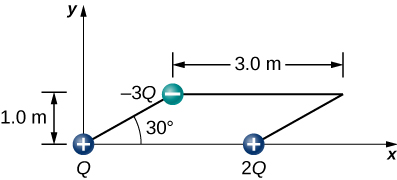
119. A positive charge q is released from rest at the origin of a rectangular coordinate system and moves under the influence of the electric field \(\displaystyle \vec{E} = E_0(1+x/a)\hat{i}.\) What is the kinetic energy of q when it passes through \(\displaystyle x=3a\)?

120. A particle of charge \(\displaystyle −q\) and mass m is placed at the center of a uniformaly charged ring of total charge Q and radius R. The particle is displaced a small distance along the axis perpendicular to the plane of the ring and released. Assuming that the particle is constrained to move along the axis, show that the particle oscillates in simple harmonic motion with a frequency \(\displaystyle f=\frac{1}{2π}\sqrt{\frac{qQ}{4πε_0mR^3}}\).

121. Charge is distributed uniformly along the entire y-axis with a density \(\displaystyle y_λ\) and along the positive x-axis from \(\displaystyle x=a\) to \(\displaystyle x=b\) with a density \(\displaystyle λ_x\). What is the force between the two distributions?

122. The circular arc shown below carries a charge per unit length \(\displaystyle λ=λ_0cosθ\), where \(\displaystyle θ\) is measured from the x-axis. What is the electric field at the origin?

123. Calculate the electric field due to a uniformly charged rod of length L, aligned with the x-axis with one end at the origin; at a point P on the z-axis.

124. The charge per unit length on the thin rod shown below is \(\displaystyle λ\). What is the electric force on the point charge q? Solve this problem by first considering the electric force \(\displaystyle d\vec{F}\) on q due to a small segment \(\displaystyle dx\) of the rod, which contains charge \(\displaystyle λdx.\) Then, find the net force by integrating \(\displaystyle d\vec{F}\) over the length of the rod.

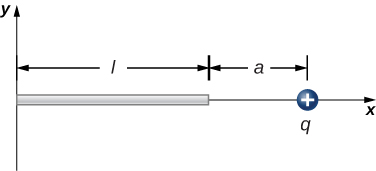
125. The charge per unit length on the thin rod shown here is \(\displaystyle λ\). What is the electric force on the point charge q? (See the preceding problem.)

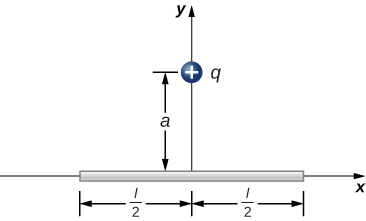
126. The charge per unit length on the thin semicircular wire shown below is \(\displaystyle λ\). What is the electric force on the point charge q? (See the preceding problems.)

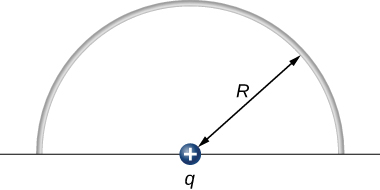
Additional Problems

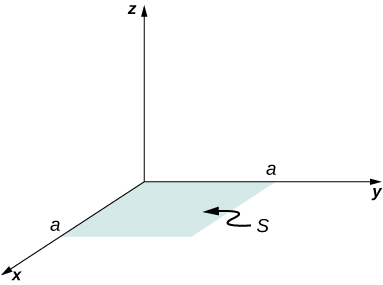
72. A vector field \(\displaystyle \vec{E}\) (not necessarily an electric field; note units) is given by \(\displaystyle \vec{E} =3x^2\hat{k}\). Calculate \(\displaystyle ∫_S\vec{E}⋅\hat{n}da\), where S is the area shown below. Assume that \(\displaystyle \hat{n}=\hat{k}\).

73. Repeat the preceding problem, with \(\displaystyle \vec{E} = 2x\hat{i}+3x^2\hat{k}\).

74. A circular area S is concentric with the origin, has radius a, and lies in the yz-plane. Calculate \(\displaystyle ∫_S\vec{E}⋅\hat{n}dA\) for \(\displaystyle \vec{E} = 3z^2\hat{i}\).

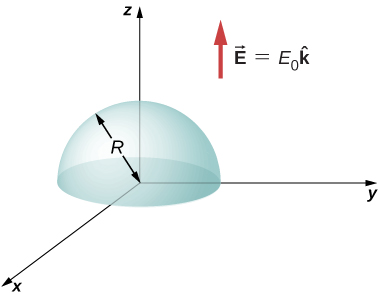
75. (a) Calculate the electric flux through the open hemispherical surface due to the electric field \(\displaystyle \vec{E} = E_0\hat{k}\) (see below).

(b) If the hemisphere is rotated by 90° around the x-axis, what is the flux through it?

76. Suppose that the electric field of an isolated point charge were proportional to \(\displaystyle 1/r^{2+σ}\) rather than \(\displaystyle 1/r^2\). Determine the flux that passes through the surface of a sphere of radius R centered at the charge. Would Gauss’s law remain valid?

77. The electric field in a region is given by \(\displaystyle \vec{E} =a/(b+cx)\hat{i}\), where \(\displaystyle a=200N⋅m/C, b=2.0m,\) and \(\displaystyle c=2.0\).What is the net charge enclosed by the shaded volume shown below?

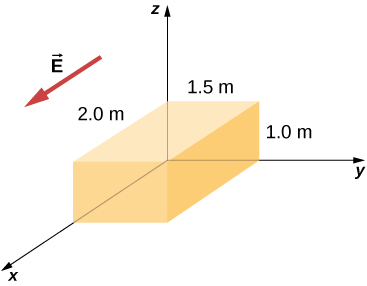
78. Two equal and opposite charges of magnitude Q are located on the x-axis at the points +a and –a, as shown below. What is the net flux due to these charges through a square surface of side 2a that lies in the yz-plane and is centered at the origin? (Hint: Determine the flux due to each charge separately, then use the principle of superposition. You may be able to make a symmetry argument.)

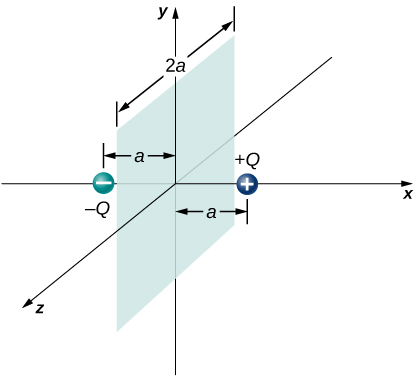
79. A fellow student calculated the flux through the square for the system in the preceding problem and got 0. What went wrong?

80. A 10cm×10cm piece of aluminum foil of 0.1 mm thickness has a charge of \(\displaystyle 20μC\) that spreads on both wide side surfaces evenly. You may ignore the charges on the thin sides of the edges.

(a) Find the charge density.

(b) Find the electric field 1 cm from the center, assuming approximate planar symmetry.

81. Two 10cm×10cm pieces of aluminum foil of thickness 0.1 mm face each other with a separation of 5 mm. One of the foils has a charge of \(\displaystyle +30μC\) and the other has \(\displaystyle −30μC\).

(a) Find the charge density at all surfaces, i.e., on those facing each other and those facing away.

(b) Find the electric field between the plates near the center assuming planar symmetry.

82. Two large copper plates facing each other have charge densities \(\displaystyle ±4.0C/m^2\) on the surface facing the other plate, and zero in between the plates. Find the electric flux through a 3cm×4cm rectangular area between the plates, as shown below, for the following orientations of the area.

(a) If the area is parallel to the plates, and

(b) if the area is tilted \(\displaystyle θ=30°\) from the parallel direction. Note, this angle can also be \(\displaystyle θ=180°+30°\).

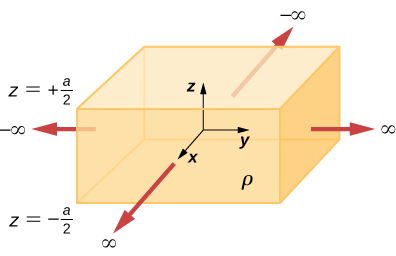
83. The infinite slab between the planes defined by \(\displaystyle z=−a/2\) and \(\displaystyle z=a/2\) contains a uniform volume charge density \(\displaystyle ρ\)(see below). What is the electric field produced by this charge distribution, both inside and outside the distribution?

84. A total charge Q is distributed uniformly throughout a spherical volume that is centered at \(\displaystyle O_1\) and has a radius R. Without disturbing the charge remaining, charge is removed from the spherical volume that is centered at \(\displaystyle O_2\) (see below). Show that the electric field everywhere in the empty region is given by \(\displaystyle \vec{E} = \frac{Q\vec{r}}{4πε_0R^3}\), where \(\displaystyle \vec{r}\) is the displacement vector directed from \(\displaystyle O_1\) to \(\displaystyle O_2\).

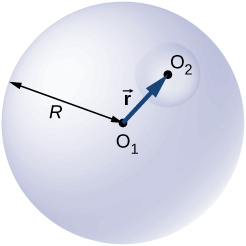
85. A non-conducting spherical shell of inner radius \(\displaystyle a_1\) and outer radius \(\displaystyle b_1\) is uniformly charged with charged density \(\displaystyle ρ_1\) inside another non-conducting spherical shell of inner radius \(\displaystyle a_2\) and outer radius \(\displaystyle b_2\) that is also uniformly charged with charge density \(\displaystyle ρ_2\). See below. Find the electric field at space point P at a distance r from the common center such that (a) \(\displaystyle r>b_2\), (b) \(\displaystyle a_2<r<b_2\), (c) \(\displaystyle b_1<r<a_2\), (d) \(\displaystyle a_1<r<b_1\), and (e) \(\displaystyle r<a_1\).

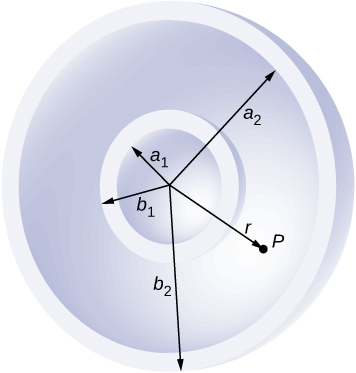
86. Two non-conducting spheres of radii \(\displaystyle R_1\) and \(\displaystyle R_2\) are uniformly charged with charge densities \(\displaystyle ρ_1\) and \(\displaystyle ρ_2\), respectively. They are separated at center-to-center distance a (see below). Find the electric field at point P located at a distance r from the center of sphere 1 and is in the direction \(\displaystyle θ\) from the line joining the two spheres assuming their charge densities are not affected by the presence of the other sphere. (Hint: Work one sphere at a time and use the superposition principle.)

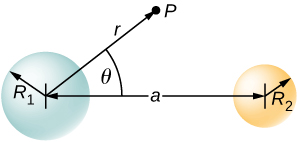
87. A disk of radius R is cut in a non-conducting large plate that is uniformly charged with charge density σ (coulomb per square meter). See below. Find the electric field at a height h above the center of the disk. (\(\displaystyle h>>R,h<<l\) or \(\displaystyle w\)). (Hint: Fill the hole with \(\displaystyle ±σ\).)

88. Concentric conducting spherical shells carry charges Q and –Q, respectively (see below). The inner shell has negligible thickness. Determine the electric field for (a) \(\displaystyle r<a;\) (b) \(\displaystyle a<r<b\); (c) \(\displaystyle b<r<c\); and (d) \(\displaystyle r>c\).

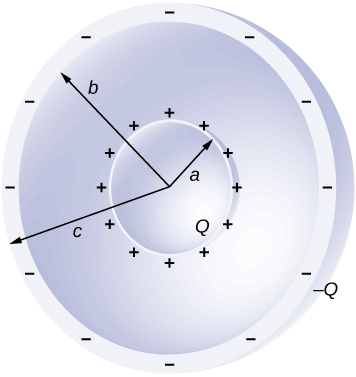
89. Shown below are two concentric conducting spherical shells of radii \(\displaystyle R_1\) and \(\displaystyle R_2\), each of finite thickness much less than either radius. The inner and outer shell carry net charges \(\displaystyle q_1\) and \(\displaystyle q_2\), respectively, where both \(\displaystyle q_1\) and \(\displaystyle q_2\) are positive. What is the electric field for (a) \(\displaystyle r<R_1\); (b) \(\displaystyle R_1<r<R_2\); and (c) \(\displaystyle r>R_2\)? (d) What is the net charge on the inner surface of the inner shell, the outer surface of the inner shell, the inner surface of the outer shell, and the outer surface of the outer shell?

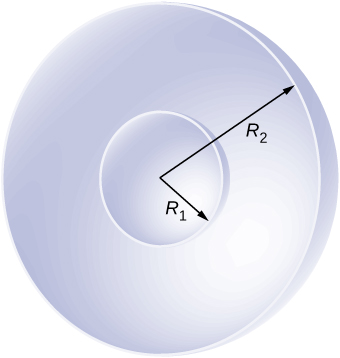
90. A point charge of q=5.0×10−8Cq=5.0×10−8C is placed at the center of an uncharged spherical conducting shell of inner radius 6.0 cm and outer radius 9.0 cm. Find the electric field at (a) r=4.0cmr=4.0cm, (b) r=8.0cmr=8.0cm, and (c) r=12.0cmr=12.0cm. (d) What are the charges induced on the inner and outer surfaces of the shell?

Challenge Problems

91. The Hubble Space Telescope can measure the energy flux from distant objects such as supernovae and stars. Scientists then use this data to calculate the energy emitted by that object. Choose an interstellar object which scientists have observed the flux at the Hubble with (for example, \(\displaystyle Vega\))³, find the distance to that object and the size of Hubble’s primary mirror, and calculate the total energy flux. (Hint: The Hubble intercepts only a small part of the total flux.)

92. Re-derive Gauss’s law for the gravitational field, with \(\displaystyle \vec{g}\) directed positively outward.

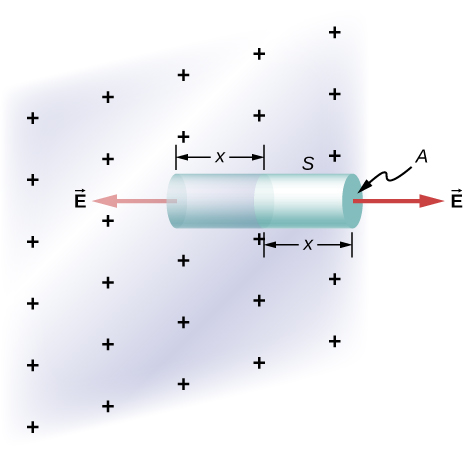
93. An infinite plate sheet of charge of surface charge density \(\displaystyle σ\) is shown below. What is the electric field at a distance x from the sheet? Compare the result of this calculation with that of worked out in the text.

94. A spherical rubber balloon carries a total charge Q distributed uniformly over its surface. At \(\displaystyle t=0\), the radius of the balloon is R. The balloon is then slowly inflated until its radius reaches 2R at the time \(\displaystyle t_0\). Determine the electric field due to this charge as a function of time

(a) at the surface of the balloon,

(b) at the surface of radius R, and

(c) at the surface of radius 2R. Ignore any effect on the electric field due to the material of the balloon and assume that the radius increases uniformly with time.

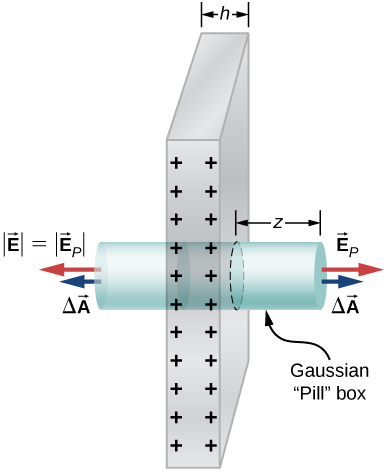
95. Find the electric field of a large conducting plate containing a net charge q. Let A be area of one side of the plate and h the thickness of the plate (see below). The charge on the metal plate will distribute mostly on the two planar sides and very little on the edges if the plate is thin.

Contributors and Attributions

Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

Contributors and Attributions

Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).