3.6: Conservation Laws

3.6.1 Potential and Kinetic Energy

One fundamental principle of physics is that momentum is always conserved in any interaction. When two objects interact, according to Newton’s third law, they exert equal and opposite forces on each other. Changes in the motion of the objects occur through conservation of momentum. If one object gains velocity, the other must lose velocity. The same applies to angular momentum, in which a rotating object cannot change its momentum unless an external twisting force (torque) acts upon it. Since the Earth experiences no such twisting force as it orbits the Sun, its revolution and orbit will continue indefinitely. However, friction from the tides is slowing the Earth’s rotation down. The tides are governed by the Moon’s gravity and since angular momentum must be conserved, as the Earth’s rotation loses angular momentum, the Moon’s orbit gains angular momentum. This results in the Moon moving further away from the Earth in its orbit by about a centimeter a year.

Like momentum, energy is also conserved. We define energy as the intangible phenomenon that can cause changes in an object’s motion, temperature, or chemical phase. For our discussion, we are going to divide energy into three categories. Kinetic energy is energy of motion. All moving objects have kinetic energy. Potential energy is energy that is stored, either by the object’s position (such as raising it to a higher elevation) or in the chemical bonds of a fuel like gasoline or sugars. Finally, radiative energy is all forms of light or electromagnetic radiation.

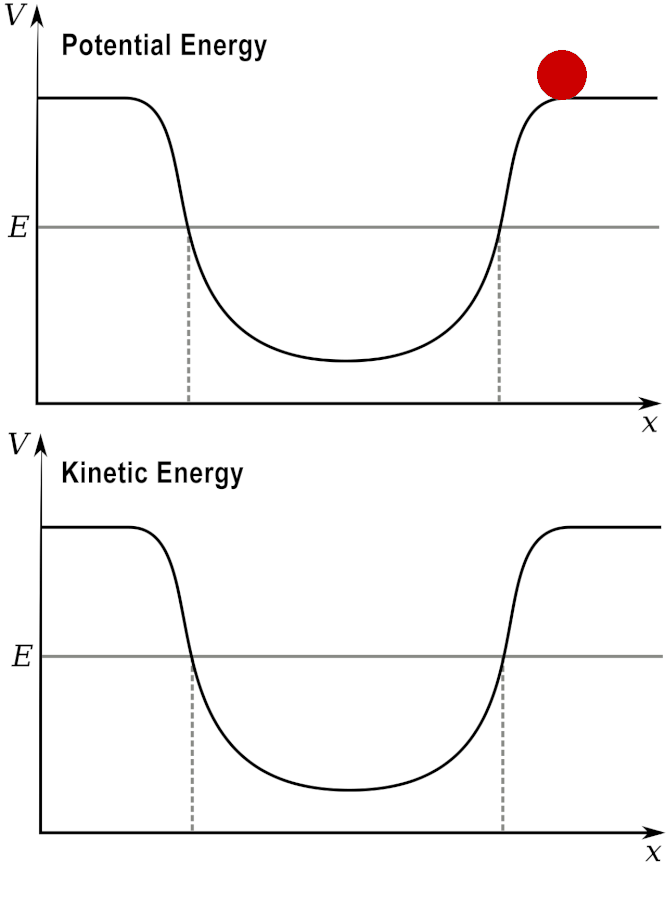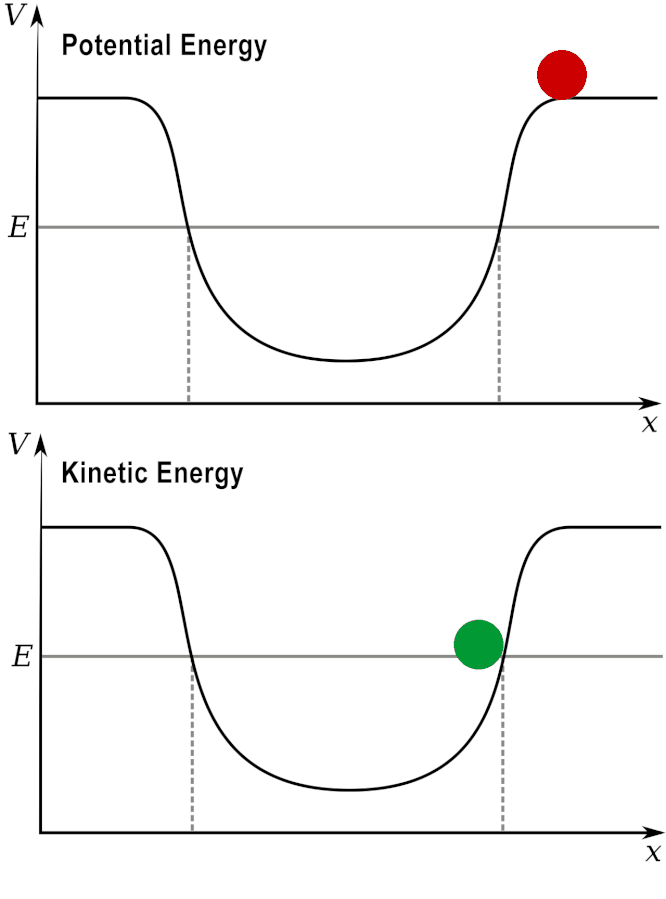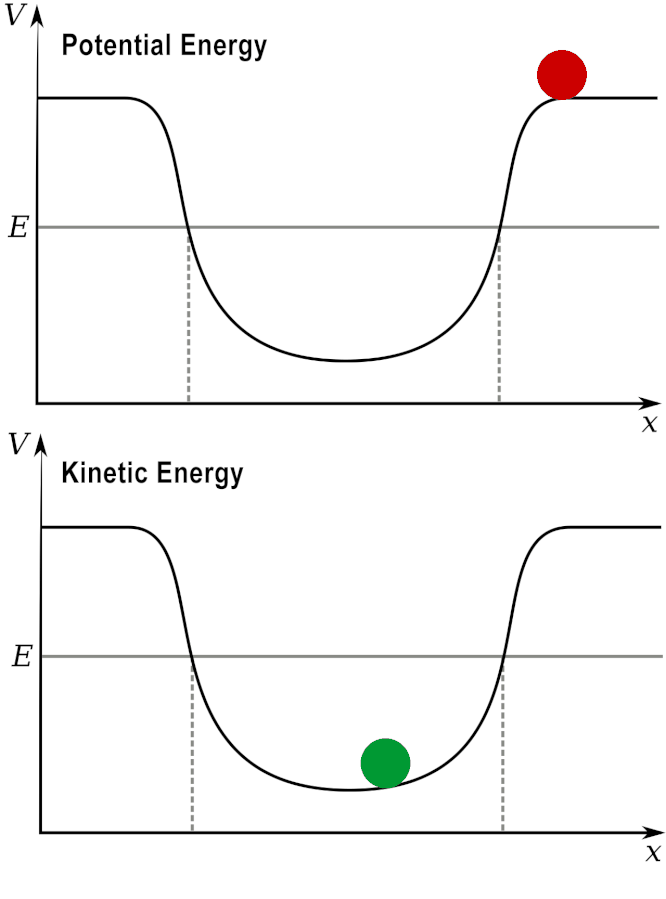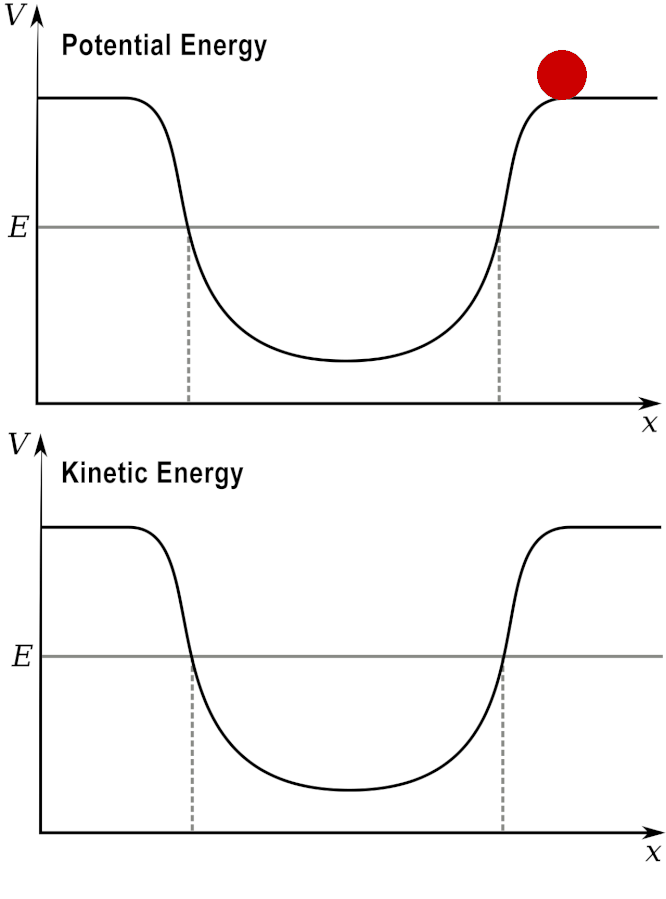Potential and Kinetic energy: A ball at a high elevation has maximum potential energy by zero kinetic energy.

As it rolls down the hill, the potential energy is converted into kinetic energy.

Benjamin J. Burger / CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0)

 

3.6.2 Measuring Temperature

Energy can make matter move or change form. It is always conserved, but it can be transformed from one form to another or transferred from one object to another. On the microscopic level, the atoms in matter, whether a solid, liquid, or gas, have kinetic energy. The collective kinetic energy of all the atoms and molecules in an object like a rock or a tank of water is called thermal energy. Usually, when we speak of thermal energy, we refer to an object’s temperature, which is defined as the average kinetic energy of all of particles in an object. Two objects can have the same temperature, but if Object A is twice as dense as Object B, then Object A also has twice as much thermal energy as Object B.

We use three different scales for measuring temperature. The Fahrenheit scale, the one most familiar to Americans, sets the freezing point of water at 32 degrees and the sea-level boiling point of water at 212 degrees. Note that these designations are arbitrary, and we can set any value to these to points. For example, the Celsius scale was designed to be simpler than the Fahrenheit scale. The Celsius scale sets the freezing point at zero degrees and the boiling point of water at 100 degrees.

However, neither of these scales are really useful in astronomy where we often study objects that are cooler than the freezing point of water. As we will see in Chapter 4, there are some equations for which negative values for temperature do not work. Therefore, we need a scale that begins at the absolute coldest point possible. At -273.15 degrees Celsius, matter (theoretically) loses all thermal energy. This point is called absolute zero is as cold as anything could possibly get in this universe. The Kelvin scale, therefore, begins at absolute zero. The increments on the Kelvin scale (scientists do not generally use the term “degrees” in the Kelvin scale) are the same size as the degrees in the Celsius scale. As a result, -273.15 degrees Celsius is equal to 0 K and 0 degrees Celsius is equal to 273.15 K. We can easily convert from Celsius to Kelvin simply by adding 273.15. For example, the sea level boiling point of water, 100 degrees Celsius is equal to 373.15 K.

3.6.3 Gravitational Potential Energy

Recall that the force of gravity an object experiences on Earth is equal to its mass times the acceleration of gravity, g. The gravitational potential energy demands on the mass, g, and how far it could fall, such as its height, h, above the ground.

PE = mgh

As an object falls, the potential energy is converted into in kinetic energy as it gathers speed, v. Kinetic energy can therefore be given with the equation:

KE = ½ mv²

For objects in space, such as a gas cloud, the gravitational potential energy depends on how it spread out its mass is. Therefore, when a cloud contracts, the gravitational potential energy is converted into thermal energy and the temperature rises.

Albert Einstein demonstrated that mass itself is a form of potential energy through his equation:

E = mc²

Where c is the speed of light. With this relationship, a small amount of mass can be converted into a large amount of kinetic or radiative energy, such as in nuclear bomb or in the core of a star. Likewise, concentrated energy in a particle accelerator can be turned into particles with mass.

Together, we use matter and energy to understand orbits. The total orbital energy, including gravitational and kinetic energy, stays constant if the orbiting object experiences no external force. Thus, orbits cannot change spontaneously. An object can gain or lose orbital energy through forces like friction. Most satellites are launched into Near Earth Orbit (NEO). NEO is not a perfect vacuum, so these satellites do experience some friction that will eventually slow them down and cause them to reenter the atmosphere. A gravitational encounter can also cause an object to gain or lose orbital energy by tugging on it.

To launch an object into out of an orbit, it must gain enough orbital energy to reach the escape velocity. For Earth, the escape velocity ≈ 11 km/s from sea level. An object launched with this speed will escape the Earth and will no longer be held in orbit around it. This is not, however, enough energy to escape the Sun’s gravity, so an object that escapes the Earth is still in orbit around the Sun.