4.5: The Doppler Effect
- Page ID
- 30876
The Doppler Effect.
https:/www.flickr.com/photos/102642344@N02/15347690967;
Ever listen to an ambulance siren as it goes by? The pitch will appear to go higher as the ambulance approaches you and then falls as it heads away from you. This is known as the Doppler effect and we experience it with any waves in which the source is moving towards or away relative to the observer, including electromagnetic waves. When the source is moving toward the observer, the successive wave fronts “bunch up” as they get emitted. This results in the wavelengths getting shorter. For light waves, this means the light waves are “blueshifted” as the color shifts towards the blue end of the spectrum. If the source is moving away from the observer, the successive wave fronts are stretched out, resulting longer wavelengths. For light, the waves are “redshifted” as the color shifts toward the red end of the spectrum. For electromagnetic waves in general, we use the terms blue shift and red shift to describe shortening or lengthening of EM waves, respectively, regardless of the original wavelength.
It does not matter whether the source of the observer is moving, the effect remains the same. Only the relative motion between source and observer matters.
The relationship between the degree of shift in wavelength to the speed of the object is found by:
Apparent wavelength/true frequency = true wavelength/apparent frequency = 1 + recession velocity/wave speed.
Since the speed of light in a vacuum, c, is a constant, the speed of the object can be found with the following equation:
Δλ/λ = v/c
Where Δλ is the change in wavelength, λ is the normal or laboratory wavelength of the light, and v is the relative speed of the source toward or away from the observer.
The Doppler effect shifts an object’s entire spectrum either toward the red or toward the blue. Thus, all the electromagnetic waves are either shortened or lengthened. For example, an object emitting radio that is moving toward us would have the radio waves shifted toward shorter wavelengths whereas an object emitting ultraviolet radiation moving away from is would have its wavelengths lengthened, perhaps into the violet or blue portions of the spectrum.
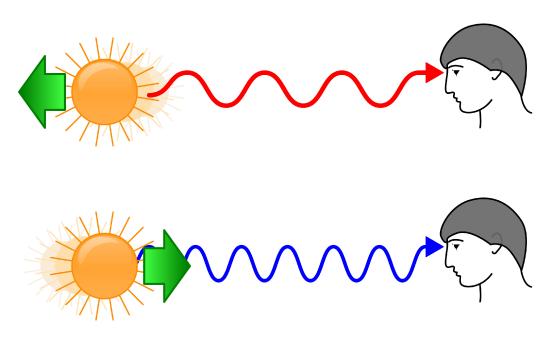Objects approaching the observer are blue shifted while objects moving away are red shifted.
This includes the emission or absorption spectral lines. Each spectral line would be shifted by the same amount, depending on the relative speed of the source. Therefore, they will still have the same relative differences in wavelength with respective to each other. As a result, we can identify the spectral lines, calculate their degree of shifting, and use that to determine the relative speed of the source.
The Doppler effect can also be used to determine the speed of rotation of a star. When a star is rotating, part of is moving toward us and part is moving away. As a result, light from one “limb” of the sphere will be blueshifted and light from the other “limb” will be redshifted. The degree of blue and red shifting depends on the rotational speed of the star, cause the spectral lines to become more spread out over a range of frequencies. The wider the spread of frequencies in the spectral lines, the faster the star’s rotation.
Finally, it is important to note that the Doppler effect only tells us how fast an object is moving toward or away from us. It tells us nothing about its motion across our field of view. If the object is moving directly toward or away from us, the Doppler effect will tell its full speed. If the object is moving across our field of view, it will tell us nothing about its motion. Finally, if the object is moving diagonally, it will only tell us the portion of the motion toward or away from us and nothing about its lateral motion.
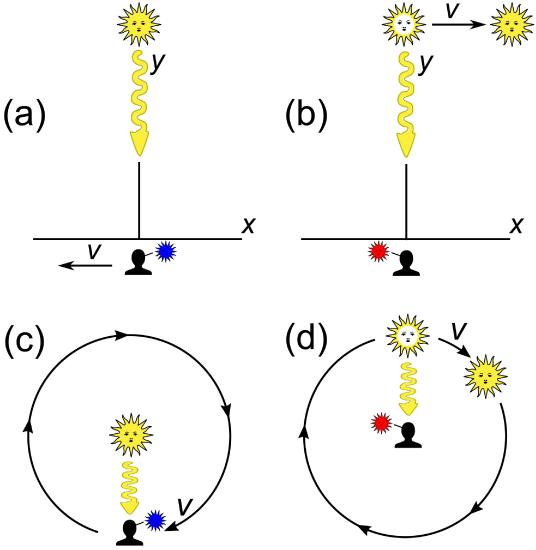The Doppler Effect does not tell us any information about an objects transverse motion relative to the observer.