10.11: Stability
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18241

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Explain the relationship between how center of mass is defined and static equilibrium
For an object to be in static equilibrium, we expect it to stay in the same state indefinitely. If it starts accelerating away from its current position, it would hardly be in equilibrium. To quantify equilibrium for a single object, there are two conditions:
- The net external force on the object is zero: ∑iFi=Fnet=0
- The net external torque, regardless of choice of origin, is also zero: ∑iri×Fi=∑iτi=τnet=0
Those two conditions hold regardless of whether the object we are talking about is a single point particle, a rigid body, or a collection of discrete particles. Being in equilibrium means that we expect no changes to the linear momentum or the angular momentum. Note that this does not mean that the system is not moving or rotating; instead it simply means that its movement will not change as time goes on.
In a special case when the external forces are governed by some potential (e.g. gravitational potential) we can gain insight into the nature of the equilibrium. From the definition of a potential we know that Fext=−dU(x)dx|x0. When the first derivative is zero, we can take the second derivative to find whether the equilibrium is stable or unstable. Explicitly, if the potential is concave-up at x0, d2U(x)dx2|x0>0, then the system is stable; conversely, if the potential is concave-down, then the equilibrium is unstable. If the second derivative is zero or does not exist, then the equilibrium is neutral—neither stable nor unstable.
Mathematically, we can view this as a Taylor series expansion on the force slightly away from equilibrium,
F(x0+δx)=F(x0)+dF(x)dx∣x0δxF(x0+δx)=−dU(x)dx∣x0+(−d2U(x)dx2∣x0)δx,
and when it is initially at equilibrium,
F(x0)=0F(x0)=0F(x0+δx)=−dU(x)dx∣x0+(−d2U(x)dx2∣x0)δxU(y)=mgy.
If the ball is at the top of the hill (where the potential is concave-down) it is possible for it to be perfectly balanced, and therefore at equilibrium. But if it gets pushed just slightly to the side, then it will roll down the hill with increasing speed, and the equilibrium is unstable.
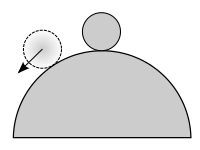
Unstable Equilibrium: A ball on top of a hill can initially be balanced, but if it moves slightly left or right, it gets pushed further and further away from the initial equilibrium position. This is an example of unstable equilibrium.
Our notion of “balance” comes directly from the formulation of equilibrium. For something to be “balanced” means that the net external forces are zero. For example, a coin could balance standing up on a table. Initially the coin will feel no net external force or torque; it is in equilibrium. But if pushed slightly to the side, it will become “off-balance,” experiencing both a force and a torque causing it to fall to the table. It might have been initially “balanced” and at equilibrium, but it was an unstable equilibrium, prone to being disturbed. But why all this talk of external forces, with no mention of internal forces? The reason is that all the internal forces must sum to zero. This follows directly from Newton’s Third Law, F12=−F21. Every time we consider a force from particle 1 on particle 2 inside of a system, we know that it will later be cancelled out by the corresponding force from particle 2 on particle 1. We could include those forces in the sum, but it is unnecessary and internal forces are often more complicated than internal forces.
This differentiation between internal and external forces is a powerful one. It also implies that you can trace the motion of the system as a whole (ignoring motion inside the system) through the net external force acting on a center of mass. A center of mass acts as if it has the entire mass of the system, located at one point, and only feels external forces. Its position is defined as the weighted average of all the particles in the system:R=∑imiri∑imi or if we have a continuous density of mass, ρ(r), then we can integrate: R=∫Vρ(r)rdV∫Vρ(r)dV. The power of the center of mass is that it hides all the details of what is happening internally. We do not always want to lose the information of what is happening internally, but it is a useful tool to remember, when dealing with a number of complicated interactions.
Key Points
- Equilibrium is defined by no net forces or torques.
- Stability of an equilibrium can be determined by the second derivative of the potential.
- Defining a center of mass allows a simple way to study the behavior of a system or object as a whole.
- Stable equilibrium requires a restoring force. This restoring force can be derived by a Taylor expansion of the force, F(x).
Key Terms
- stable equilibrium: The response [of a system in static equilibrium] to a small perturbation is forces that tend to restore the equilibrium.
- center of mass: The center of mass (COM) is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero.
- static equilibrium: the physical state in which all components of a system are at rest and the net force is equal to zero throughout the system
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Mechanical equilibrium. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_equilibrium. License: CC BY-SA: Attribution-ShareAlike
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY-SA: Attribution-ShareAlike
- Center of mass. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Center_of_mass. License: CC BY-SA: Attribution-ShareAlike
- Mechanical equilibrium. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_equilibrium. License: CC BY-SA: Attribution-ShareAlike
- stable equilibrium. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/stable%20equilibrium. License: CC BY-SA: Attribution-ShareAlike
- center of mass. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/center%20of%20mass. License: CC BY-SA: Attribution-ShareAlike
- static equilibrium. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/static_equilibrium. License: CC BY-SA: Attribution-ShareAlike
- Unstable equilibrium. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:Unstable_equilibrium.svg. License: Public Domain: No Known Copyright

