10.14: Elasticity, Stress, Strain, and Fracture
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18244

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Identify properties of elastic objects
We now move from consideration of forces that affect the motion of an object (such as friction and drag) to those that affect an object’s shape. If a bulldozer pushes a car into a wall, the car will not move once it hits the wall, but it will noticeably change shape. A change in shape due to the application of a force is a deformation. Even very small forces are known to cause some deformation. For small deformations, two important characteristics are observed. First, the object returns to its original shape when the force is removed—that is, the deformation is elastic for small deformations. Second, the size of the deformation is proportional to the force—that is, for small deformations, Hooke’s law is obeyed. In equation form, Hooke’s law is given by F=kΔL, where ΔL is the change in length.
Elasticity is a measure of how difficult it is to stretch an object. In other words it is a measure of how small kk is. Very elastic materials like rubber have small kk and thus will stretch a lot with only a small force.
Stress is a measure of the force put on the object over the area.
Strain is the change in length divided by the original length of the object.
Experiments have shown that the change in length (ΔL) depends on only a few variables. As already noted, ΔL is proportional to the force F and depends on the substance from which the object is made. Additionally, the change in length is proportional to the original length L0 and inversely proportional to the cross-sectional area of the wire or rod. For example, a long guitar string will stretch more than a short one, and a thick string will stretch less than a thin one.
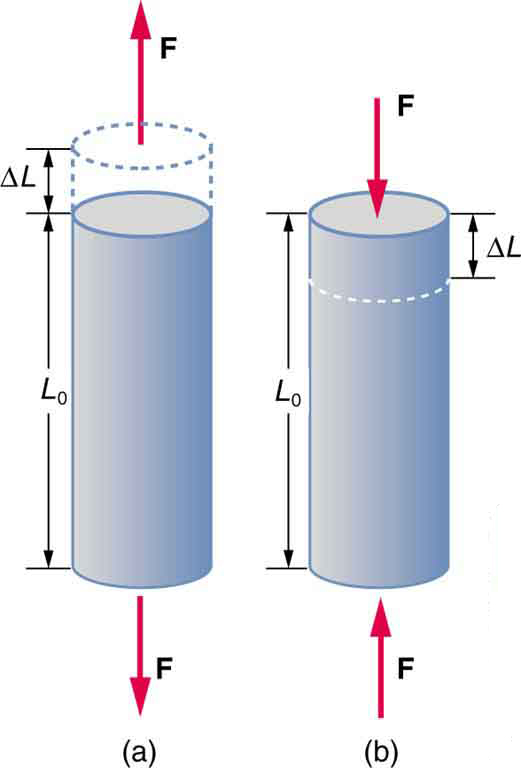
Tension/Compression: Tension: The rod is stretched a length ΔL when a force is applied parallel to its length. (b) Compression: The same rod is compressed by forces with the same magnitude in the opposite direction. For very small deformations and uniform materials, ΔL is approximately the same for the same magnitude of tension or compression. For larger deformations, the cross-sectional area changes as the rod is compressed or stretched.
Fracture
Fracture is caused by a strain placed on an object such that it deforms beyond its elastic limit and breaks.
learning objectives
- Relate fracture with the elastic limit of a material
Materials cannot stretch forever. When a strain is applied to a material it deforms elastically proportional to the force applied. However, after it has deformed a certain amount, the object can no longer take the strain and will break or fracture. The zone in which it bends under strain is called the elastic region. In that region the object will bend and then return to its original shape when the force is abated. Past that point, if more strain is added, the object may permanently deform and eventually fracture.
Fracture strength, also known as breaking strength, is the stress at which a specimen fails via fracture. This is usually determined for a given specimen by a tensile test, which charts the stress-strain curve. The final recorded point is the fracture strength.
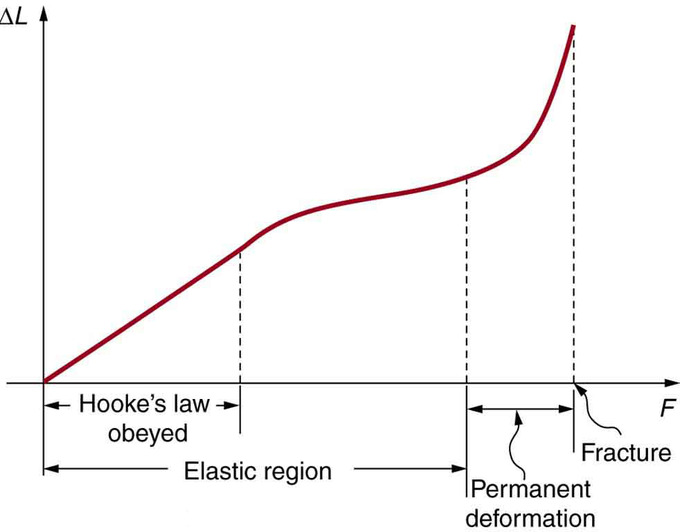
Fracture: This is a graph of deformation ΔL versus applied force F. The straight segment is the linear region where Hooke’s law is obeyed. The slope of the straight region is 1k. For larger forces, the graph is curved but the deformation is still elastic—L will return to zero if the force is removed. Still greater forces permanently deform the object until it finally fractures. The shape of the curve near fracture depends on several factors, including how the force F is applied. Note that in this graph the slope increases just before fracture, indicating that a small increase in F is producing a large increase in L near the fracture.
Bones, on the whole, do not fracture due to tension or compression. Rather they generally fracture due to sideways impact or bending, resulting in the bone shearing or snapping. The behavior of bones under tension and compression is important because it determines the load the bones can carry. Bones are classified as weight-bearing structures such as columns in buildings and trees. Weight-bearing structures have special features; columns in building have steel-reinforcing rods while trees and bones are fibrous. The bones in different parts of the body serve different structural functions and are prone to different stresses. Thus, the bone in the top of the femur is arranged in thin sheets separated by marrow while, in other places, the bones can be cylindrical and filled with marrow or just solid. Overweight people have a tendency toward bone damage due to sustained compressions in bone joints and tendons.
Key Points
- Elasticity is a measure of the deformation of an object when a force is applied. Objects that are very elastic like rubber have high elasticity and stretch easily.
- Stress is force over area.
- Strain is change in length over original length.
- Most objects behave elastically for small strains and return to their original shape after being bent.
- If the strain on an object is greater than the elastic limit of the object, it will permanently deform or eventually fracture.
- Fracture strength is a measure of the force needed to break an object.
Key Items
- deformation: A transformation; change of shape.
- strain: The amount by which a material deforms under stress or force, given as a ratio of the deformation to the initial dimension of the material and typically symbolized by ε is termed the engineering strain. The true strain is defined as the natural logarithm of the ratio of the final dimension to the initial dimension.
- elastic: Capable of stretching; particularly, capable of stretching so as to return to an original shape or size when force is released.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, Elasticity: Stress and Strain. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42081/latest/. License: CC BY: Attribution
- deformation. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/deformation. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Elasticity: Stress and Strain. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42081/latest/. License: CC BY: Attribution
- Fracture. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Fracture. License: CC BY-SA: Attribution-ShareAlike
- strain. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/strain. License: CC BY-SA: Attribution-ShareAlike
- elastic. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/elastic. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Elasticity: Stress and Strain. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42081/latest/. License: CC BY: Attribution
- OpenStax College, Elasticity: Stress and Strain. February 9, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42081/latest/Figure_06_03_01a.jpg. License: CC BY: Attribution

