1.2: Dynamics
( \newcommand{\kernel}{\mathrm{null}\,}\)
Dynamics
Concepts and Principles
Newton’s First Law
Dynamics is the study of the cause of motion, or more precisely the cause of changes in motion. In the late 1600’s Isaac Newton hypothesized that motion does not require a cause, rather changes in motion require causes. An object experiences a change in motion only when it interacts with some aspect of its surroundings. This bold hypothesis, referred to as Newton’s First Law of Motion, is summarized by the idea that an object will maintain its state of motion, whether at rest or traveling at high speed, unless acted upon by some aspect of its surroundings.
Using the kinematic terminology developed in the last unit, this means that an object’s velocity (state of motion) is constant unless it interacts with some outside agent. An external interaction is not necessary for an object to move, it is only necessary if the object’s velocity changes. Thus, what is caused is not velocity, but acceleration. This concept is one of the most subtle, and complex, in all of physics.
Newton’s Second Law
Newton also hypothesized that the sum total of all interactions with the external environment, which he termed forces, is directly proportional to the acceleration of the object. Moreover, the proportionality constant between the sum of all forces acting on an object and the acceleration of the object measures the “resistance” of an object to changes in its motion. This resistance to changes in motion is termed the inertia.
For example, an object with great inertia (quantified by a large proportionality constant) responds to the application of forces with a relatively small acceleration. An object with little inertia (a small proportionality constant) responds to the application of the same forces with a relatively large acceleration. The amount of inertia an object has is measured by the inertial mass of the object.
In summary, this relationship, known as Newton’s Second Law of Motion, and can be written mathematically as:

where
- F is a force acting on the object from its surroundings, measured in Newtons (N),
- S (sigma) is a shorthand reminder to sum all of the forces acting on the object,
- and m is the mass of the object, measured in kilograms (kg).
The sum of all of the forces acting on an object will be referred to as the total force acting on the object.
Newton’s Third Law
Newton’s third great contribution to the study of dynamics was his vision of force, defined to be the interaction between an object and some aspect of its surroundings. Newton theorized that since objects interact with other objects in their surroundings, always in pairs, a certain symmetry exists in nature. The distinction between the actor and the acted-upon is arbitrary. It would be just as easy to switch focus and consider the object in the surroundings as the acted-upon and the original object of interest the actor.
If nature exhibits this symmetry, then the force that one object exerts on another must always be equal in magnitude to the force that the second object exerts on the first. To speak of one object as exerting a force on another is to speak of only one-half of the picture. This idea, known as Newton’s Third Law of Motion, is of central importance in the study of forces. In summary, objects interact with each other, and equal magnitude forces are exerted on each of the two objects interacting. A simplistic way of picturing this is the idea that you cannot touch something without being touched, and moreover that the harder you touch the harder you will be touched in return.
Investigating the dynamics of a situation involves the identification of all interactions an object experiences with other objects in its surroundings. To help in the identification of these interactions, and to use this information to better describe the ultimate motion of the object, a number of useful analysis tools are detailed below.
Analysis Tools
Drawing Free-Body Diagrams
The free-body diagram is by far the most important analysis tool for determining the interactions between an object and its surroundings. There are three distinct steps to creating a free-body diagram. Let’s walk through the steps for the situation described below:
A child pulls herself up a rope using only her hands.
1. Select the object you would like to study.
In this example, it is probably safe to assume that the object we would like to study is the child. However, depending on what we are investigating it may be the rope or even the ceiling we are interested in. Selecting the correct object to represent by a free-body diagram is a crucial step, especially in more complicated situations. With practice you will develop a knack for selecting the correct object to represent.
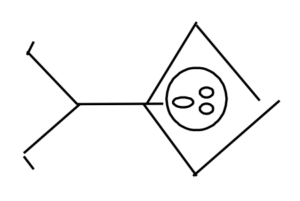
2. Draw a picture of the object of interest free from all other objects.
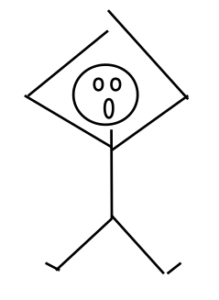 | Notice that the rope does not appear in the diagram. As the name free-body implies, the object is drawn free of all external constraints. |
3. Indicate on the diagram all interactions of the object with its environment.
Now comes the most difficult part of constructing a free-body diagram. It is crucial not to miss an interaction. If an interaction is overlooked, than the total of the forces will be incorrect, and the acceleration will be incorrect, and your entire analysis will be incorrect.
Also, only the portion of the interaction that acts on the girl should be indicated on a free-body diagram of the girl. For example, she is interacting with the rope. The rope’s action on the girl will be indicated, not the action of the girl on the rope.
To aid in the search for interactions, we will divide the types of interactions that the girl can be part of into two types, non-contact and contact.
- Non-Contact Interactions
Non-contact interactions include all interactions that can occur between the girl and objects in her surroundings that do not require direct physical contact between the two objects. Non-contact interactions include the interaction of the girl with the gravitational and electromagnetic fields in her vicinity. (How these fields are created and how they can affect the girl will slowly be incorporated into our physics model.)
At the current level of complexity, however, the only non-contact interaction you need worry about is the interaction of the girl with the gravitational field created by the earth, which we will simply term the force of gravity. The direction of this force is down, toward the center of the earth.
- Contact Interactions
Contact interactions occur at every point on the girls’ body in which she is in direct physical contact with an external object. The most obvious of these is the rope. The girl is in contact with the rope, so the rope and girl exert forces on each other. These forces are equal in magnitude. Remember, however, that it is only the force exerted on the girl that is indicated on a free-body diagram of the girl. The location of this force is at the girls’ hands, and the direction of this force is up. (The direction of this force cannot be down, because that would imply that the rope is pushing the girl, as opposed to pulling her. It is impossible for a rope to push someone, unless it is a very stiff rope. Very stiff ropes will be called rods.)
The only other objects to actually make contact with the girl are air molecules. The air molecules interact with the girl on all sides, each exerting a small force directly inward, perpendicular to the girl’s body. Although each of these forces is very small, their sum is not always small. For example, if the girl were falling freely from an airplane the vast numbers of air molecules colliding with the girl from underneath, versus the rather small number colliding from above, and the strength of these collisions, would add to a very large force acting upward on the girl. This force could easily be equal in magnitude to the force of gravity on the girl. The force of air molecules on an object, referred to as air resistance, is often ignored in analyzing scenarios simply because of the difficulty of dealing with the complexity.
However, in many cases the effects of the air molecules are negligible compared to the other forces acting on the object. This is the case with the girl climbing the rope. The forces exerted by the air molecules are probably very close to being uniformly distributed around the girl’s surface. Thus, for every air molecule pushing her to the right, there is probably an air molecule pushing her to the left. These forces will add to a total force very close to zero.
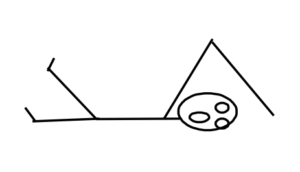
A correct free-body diagram for the girl is shown below:
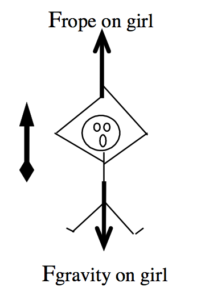 |
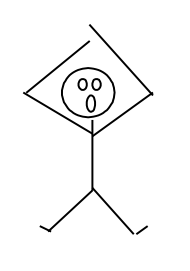
Since a coordinate system is crucial for translating motion diagrams and free-body diagrams into mathematical relationships, a coordinate system has been added to the free-body diagram. It is always a good idea to use the same coordinate system for both the free-body diagram and the motion diagram.
|
Calculating the Force of Gravity near the Surface of the Earth
In addition to creating the three laws of motion mentioned earlier, Newton also postulated the Law of Universal Gravitation. This law states that every object of mass in the universe creates a gravitational field, and every object of mass in the universe senses and interacts with every other objects’ field. That’s an awful lot of forces! To try to identify and estimate the magnitude of all of these forces on an object near the surface of the earth would be a lifelong task.
Luckily, the strength of the gravitational field depends on the mass of the object producing the field, and inversely as the square of the distance from the object. The more massive the object, the stronger the field. The closer the object, the stronger the field. Thus, since the earth is much more massive than any other nearby object, when creating free-body diagrams for objects near the surface of the earth we can safely include just the gravitational field due to the earth, ignoring all the other, relatively small, gravitational fields.
The magnitude of the gravitational field of a massive object (g) depends on the mass of the object (M), the distance from the center of the object (d), and a constant called, appropriately, the gravitational constant (G). The relationship is:

Near the surface of the earth, the gravitational field has a magnitude of approximately 9.8 N/kg. Although the gravitational field strength varies with the distance from the surface of the earth, we will ignore this slight variation unless explicitly told to include its effects.
The gravitational force felt by a massive object in the presence of a gravitational field is given by the product of the object’s mass and the magnitude of the gravitational field at the location of the object:
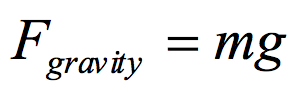
Applying Newton’s Second Law
Let’s return to the scenario under investigation and make some quantitative information more explicit. Then, we can attempt to further investigate the situation using Newton’s Second Law.
A 30 kg child pulls herself up a rope at approximately constant speed using only her hands.
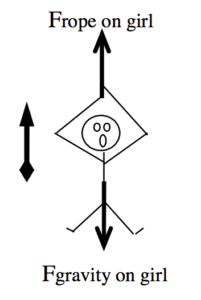 | Newton’s Second Law states: 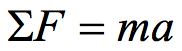 refers to the sum of all of the forces acting on the girl, the force of the rope (which is positive in our coordinate system) and the force of gravity (which is negative in our coordinate system). Thus, 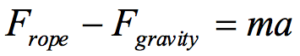 Since m = 30 kg, and a = 0 m/s2 (since she climbs at constant speed), the equation becomes: 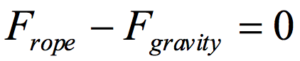 By Newton’s relationship for the force of gravity: 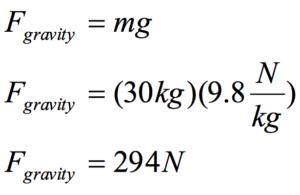 Therefore:
|
Thus, Newton’s Second Law allows us to determine the force with which the rope pulls on the girl. Of course, by Newton’s Third Law, the force with which the girl pulls on the rope is equal in magnitude, so the girl exerts a 294 N force on the rope.
If the girl had not climbed the rope at approximately constant speed her acceleration would have to be determined, either from an explicit mention in the description or through using the kinematic relations developed in the last unit, and then inserted into Newton’s Second Law. If her acceleration had been directed upwards (positive) the force of the rope on the girl would have had to be larger. If her acceleration had been directed downwards (negative) the force of the rope on the girl would have had to be smaller.
Analyzing a More Complex Scenario
Before you start analyzing dynamics scenarios on your own, let’s work our way through a more complex scenario.
To practice falling, a 55 kg pole-vaulter falls from rest off of a wall 5.0 m above a foam cushion. The pole-vaulter sinks about 1.8 m into the cushion before stopping.
Before we begin analyzing the forces acting on this pole-vaulter, I think we should try to get a handle on the kinematics of the situation. Therefore, our first step in analyzing this situation is to draw a motion diagram and tabulate motion information.
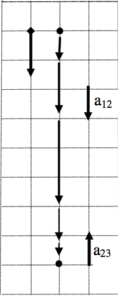 | Event 1: The instant she leaves the wall. t1 = 0 s r1 = 0 m v1 = 0 m/s a12 =
| Event 2: The instant she hits the cushion. t2 = r2 = 5.0 m v2 = a23 =
| Event 3: The instant she comes to rest. t3 = r3 = 6.8 m v3 = 0 m/s
|
Notice that between the instant she leaves the wall and the instant she hits the cushion the acceleration is positive (down), while between the instant she hits the cushion and the instant she comes to rest the acceleration is negative (up). Thus, when applying the kinematic relationships and Newton’s Second Law we will have to be careful not to confuse variables between these two intervals.
What should jump out at you is the fact that this kinematic scenario cannot be solved! There are five unknown kinematic quantities and only four kinematic equations. Something else is needed in order to complete the kinematic description. Let’s look at the forces acting on the pole-vaulter to see if we can figure out another piece of kinematic information.
Between the first two instants, the only force acting on the pole-vaulter is the force of gravity. Once she hits the cushion, however, there are two forces acting on the pole-vaulter, the force of gravity and the force of the cushion. Correct free-body diagrams for these two distinct phases of her motion are given below.

The diagram on the left corresponds to the first time interval and the diagram on the right to the second time interval. For each of these free-body diagrams, I will apply Newton’s Second Law:

Thus, from Newton’s Second Law, we know that the acceleration during the fall is 9.8 m/s2. (We still don’t know what the acceleration was during the impact portion of the motion.) Substituting this value back into the motion table yields:
| Event 1: The instant she leaves the wall. t1 = 0 s r1 = 0 m v1 = 0 m/s a12 = 9.8 m/s2 | Event 2: The instant she hits the cushion. t2 = r2 = +5.0 m v2 = a23 = | Event 3: The instant she comes to rest. t3 = r3 = +6.8 m v3 = 0 m/s |
This is now solvable, using strictly kinematics, for the four remaining unknowns. Try to do the math on your own, and compare your result to:
| Event 1: The instant she leaves the wall. t1 = 0 s r1 = 0 m v1 = 0 m/s a12 = 9.8 m/s2 | Event 2: The instant she hits the cushion. t2 = 1.0 s r2 = +5.0 m v2 = +9.9 m/s a23 = -27 m/s2 | Event 3: The instant she comes to rest. t3 = 1.36 s r3 = +6.8 m v3 = 0 m/s |
We now have a complete kinematic description of the motion.
Returning to Newton’s Second Law for the impact portion of the motion,

The cushion exerts a force of about 2000 N on the pole-vaulter to stop her fall.
Hints and Suggestions
The Magnitude of the Gravitational Field
Quite often, students make a pair of mistakes when dealing with the magnitude of the gravitational field, g.
1. ‘g’ is never negative.
Since g is the magnitude of the gravitational field, it cannot be a negative number. As a magnitude, it does not have a direction associated with it! Resist all temptation to replace ‘g’ with the value “-9.8 N/kg”!
Part of the confusion lies with the fact that the gravitational field does have an associated direction. The gravitational field of the earth is directed downward toward the center of the earth. Even so, the gravitational field is not negative. Negative only makes sense relative to a coordinate system, and since you are always free to choose any system you want, the gravitational field is just as likely to be oriented in the positive as the negative direction.
2. ‘g’ is not an acceleration.
Often, students have learned that ‘g’ is the “acceleration due to gravity.” However, as I sit here in a chair writing this book, the force of gravity is acting on me and I am most definitely not accelerating at 9.8 m/s2! In fact, the force of gravity has acted on me for every second of my life and only very rarely have I accelerated at 9.8 m/s2. ‘g’ measures the strength of the gravitational field. As such, it is related to the gravitational force, which, like all forces, can give raise to accelerations. However, it is the total force acting on an object that determines its acceleration, not simply the force of gravity.
It is true that the units of ‘g’, N/kg, are also the units of acceleration, since a Newton is defined to be a kg m/s2. It is also true that in a very specific scenario[1], when the only force acting on an object is the force of gravity, the magnitude of the object’s acceleration is numerically equal to ‘g’. However, there are also very specific scenarios in which the acceleration of an object is numerically equal to 4.576 m/s2, or 62.31452 m/s2. The strength of physics is its ability to analyze diverse scenarios with the same small set of tools, not to develop specialized tools tailored to every different specific scenario. Newton’s Second Law will always allow you to determine an object’s acceleration, whether the force of gravity acts alone or not.
Newton’s Third Law
Many physics students have heard the saying, “For every action there is an equal and opposite re-action.” I was forced to memorize this statement in a middle-school science class, and was told it was called Newton’s Third Law. I’m sure I had no idea what it really meant. It states that there is a reaction to every action, which seems to imply the “action” happens first. This isn’t what the law means. There really is no separation or possible distinction between action and reaction. A better way to look at it is that there is an interaction between two objects, and the two “sides” of this interaction experience exactly the same force. Of course, the effect of this mutually symmetrical force acting on the two objects need not be identical.
As a test of your understanding of Newton’s Third Law, try to answer the following question:
As you drive along the highway, a mosquito splats against your car windshield. During the collision between the mosquito and the car,
a. the force on the mosquito was greater in magnitude than the force on the car.
b. the force on the car was greater in magnitude than the force on the mosquito.
c. the force on the mosquito was equal in magnitude to the force on the car.
d. it is impossible to determine the relative sizes of the forces without more information.
As strange as it may seem, the correct answer is ‘c’. The forces exerted on the mosquito and the car are equal in magnitude. In the terminology used in this chapter, the mosquito and car interact (probably an unpleasant interaction for the mosquito), and in an interaction the two agents involved exert equal forces on each other.
However, obviously something is different about the interaction from the mosquito’s perspective. What is different is not the force acting on the mosquito but rather its acceleration. Although the forces acting on the mosquito and car are the same, the mosquito’s acceleration is much greater than the car’s acceleration because the mosquito’s mass is much smaller than the car’s mass. The acceleration of the car is so small that it is not even noticed by the driver, while the acceleration of the mosquito is certainly noticed by the mosquito!
Activities
Construct free-body diagrams for the objects described below.
a. When throwing a ball vertically upward, my hand moves through a distance of about 1.0 m before the ball leaves my hand. The 0.80 kg ball reaches a maximum height of about 20 m above my hand.
while the ball is in my hand  | after the ball leaves my hand
|
b. To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a 2.0 m thick foam cushion resting on the ground. However, he misses the cushion.
while falling through the air
| while being stopped by the ground |
c. A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light.
the top light  | the bottom light
|
Construct free-body diagrams for the objects described below.
a. A 4000 kg rocket’s engine produces a thrust of 70,000 N for 15 s. The rocket is fired vertically upward.
while the engine is firing  | after the engine turns off
|
b. Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. An 84 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the 84 kg block is released, the student is pulled up to his dorm room.
the student | the block
|
c. A 1.0 kg block is stacked on top of a 2.0 kg block on the floor of an elevator moving downward at constant speed.
the 1.0 kg block  | the 2.0 kg block
|
A block hangs from the ceiling of an elevator by a string. For each of the following situations, circle the correct relationship symbol between the magnitude of the force of the string on the block and the magnitude of the force of gravity on the block and explain your reasoning.
a. The elevator is at rest.

b. The elevator is moving upward at an constant speed.
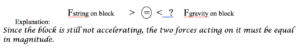 c. The elevator is moving downward at a decreasing speed.
c. The elevator is moving downward at a decreasing speed.

d. The elevator is moving upward at an increasing speed.

A man stands on a bathroom scale inside of an elevator. For each of the following situations, circle the correct relationship symbol between the magnitude of the force of the scale on the man and the magnitude of the force of gravity on the man and explain your reasoning.
a. The elevator is at rest.
Fscale on man > = < ? Fgravity on man
Explanation:
b. The elevator is moving downward at a constant speed.
Fscale on man > = < ? Fgravity on man
Explanation:
c. The elevator is moving downward at a increasing speed.
Fscale on man > = < ? Fgravity on man
Explanation:
d. The elevator is moving upward at a decreasing speed.
Fscale on man > = < ? Fgravity on man
Explanation:
Two blocks are stacked on top of each other on the floor of an elevator. For each of the following situations, circle the correct relationship symbol between the two force magnitudes and explain your reasoning.
a. The elevator is moving downward at a constant speed.
Fbottom block on top block > = < ? Ftop block on bottom block
Explanation:
Fbottom block on top block > = < ? Fgravity on top block
Explanation:
b. The elevator is moving downward at an increasing speed.
Fbottom block on top block > = < ? Ftop block on bottom block
Explanation:
Fbottom block on top block > = < ? Fgravity on top block
Explanation:
c. The elevator is moving upward at a decreasing speed.
Fbottom block on top block > = < ? Ftop block on bottom block
Explanation:
Fbottom block on top block > = < ? Fgravity on top block
Explanation:

If the graph is of position vs. time, rank these graphs on the basis of the total force acting on the object.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
If the graph is of velocity vs. time, rank these graphs on the basis of the total force acting on the object.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are six automobiles traveling at constant velocity. The automobiles have different masses and velocities. Rank these automobiles on the basis of the magnitude of the total force acting on them.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
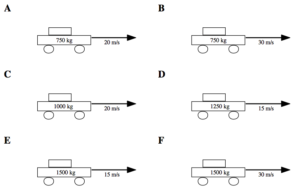
Below are six identical baseballs shortly after being thrown. At the instant shown, the baseball’s velocity is indicated, along with the distance the ball has traveled and the elapsed time since leaving the thrower’s hand. Rank these baseballs on the basis of the magnitude of the force of the thrower’s hand currently acting on them.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are three blocks stacked on top of each other at rest. Rank the magnitude of the forces referred to below from largest to smallest.

A The force of the 3 kg block on the 2 kg block
B The force of the 2 kg block on the 3 kg block
C The force of the 3 kg block on the 1 kg block
D The force of the 1 kg block on the 3 kg block
E The force of the 2 kg block on the 1 kg block
F The force of the 1 kg block on the 2 kg block
G The force of the 1 kg block on the floor
H The force of the floor on the 1 kg block
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ 7. _____ 8. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are three blocks stacked on top of each other inside of an elevator moving upward at increasing speed. Rank the magnitude of the forces referred to below from largest to smallest.

A The force of the 3 kg block on the 2 kg block
B The force of the 2 kg block on the 3 kg block
C The force of the 3 kg block on the 1 kg block
D The force of the 1 kg block on the 3 kg block
E The force of the 2 kg block on the 1 kg block
F The force of the 1 kg block on the 2 kg block
G The force of the 1 kg block on the floor of the elevator
H The force of the floor of the elevator on the 1 kg block
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ 7. _____ 8. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
For each of the collisions illustrated below, circle the correct relationship symbol between the magnitude of the force of car A on car B and the magnitude of the force of car B on car A and explain your reasoning.
a.
Fcar A on car B > = < ? Fcar B on car A Explanation:
|
b.
Fcar A on car B > = < ? Fcar B on car A Explanation:
|
c.
Fcar A on car B > = < ? Fcar B on car A Explanation:
|
A 100 kg man concerned about his weight decides to weigh himself in an elevator. He stands on a bathroom scale in an elevator that is moving upward at 3.0 m/s. As the elevator reaches his floor, it slows to a stop over a distance of 2.0 m.

A 40 kg child is hanging from a rope by her hands. She exerts a burst of strength and 2.0 s later is traveling at 1.4 m/s up the rope.
Motion Diagram Motion Information Free-Body Diagram
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
|
Mathematical Analysis[i]
A 55 kg pole-vaulter, just before touching the cushion on which she lands after a jump, is falling downward at a speed of 10 m/s. The pole-vaulter sinks about 2.0 m into the cushion before stopping.
Motion Diagram Motion Information Free-Body Diagram
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
|
Mathematical Analysis[ii]
A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light. The elevator is moving downward at 4.0 m/s when someone presses the emergency stop button. The elevator comes to rest in 1.2 seconds.

A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light. The elevator is moving downward at 4.0 m/s when someone presses the emergency stop button. During the stop, the upper cable snaps. The elevator engineer says that the cable could withstand a force of 40 N without breaking.
Motion Diagram Motion Information Free-Body Diagrams
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| the top light
the bottom light
|
Mathematical Analysis[iii]
A 70 kg student is 120 m above the ground, moving upward at 3.5 m/s, while hanging from a rope hanging from a 280 kg helium balloon. The lift on the balloon due to the buoyant force is 3000 N.
Motion Diagram Motion Information Free-Body Diagrams
| Mathematical Analysis[iv]
| Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| student
balloon
|
To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a foam cushion. The pole-vaulter sinks about 1.4 m into the cushion before stopping.
Motion Diagram Motion Information Free-Body Diagrams
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3:
t3 = r3 = v3 =
| before hitting cushion
after hitting cushion |
Mathematical Analysis[v]
To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a 2.0 m thick foam cushion resting on the ground. However, he misses the cushion. The pole-vaulter sinks about 0.10 m into the ground before stopping.
Motion Diagram Motion Information Free-Body Diagrams
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3:
t3 = r3 = v3 =
| before hitting cushion
after hitting ground |
Mathematical Analysis[vi]
When throwing a 0.80 kg ball vertically upward, my hand moves through a distance of about 1.0 m before the ball leaves my hand. The ball leaves my hand at 35 m/s.
Motion Diagram Motion Information Free-Body Diagrams
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3: Ball reaches its max height
t3 = r3 = v3 =
| before ball leaves hand
after ball leaves hand
|
Mathematical Analysis[vii]
A 4000 kg rocket’s engine produces a thrust of 70,000 N for 15 s. The rocket is fired vertically upward.
Motion Diagram Motion Information Free-Body Diagrams
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3: Rocket reaches its max height
t3 = r3 = v3 =
| before engine turns off
after engine turns off |
Mathematical Analysis[viii]
Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. An 84 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the 84 kg block is released, the student is pulled up to his dorm room, 8.0 m off the ground.

Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. A block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room, 8 m off the ground, in a time of 1.8 s.
Motion Diagram Motion Information Free-Body Diagrams
 | Object: Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| student
block
|
Mathematical Analysis[ix]
Tired of walking down the stairs, an 80 kg engineering student designs an ingenious device for reaching the ground from his third floor dorm room. A block, at rest on the ground, is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the student steps out of the window, she falls the 8 m to the ground in a time of 1.8 s.
Motion Diagram Motion Information Free-Body Diagrams
 | Object: Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| student
block
|
Mathematical Analysis[x]
| A 60 kg student lifts herself from rest to a speed of 1.5 m/s in 2.1 s. The chair has a mass of 35 kg. |  |
Motion Diagram Motion Information Free-Body Diagrams
 | Object: Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| student
chair
|
Mathematical Analysis[xi]
| A 60 kg student lowers herself down 40 m at a constant speed of 1.0 m/s. The chair has a mass of 35 kg. |  |
Motion Diagram Motion Information Free-Body Diagrams
 | Object: Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| student
chair
|
Mathematical Analysis[xii]
A man of mass m, concerned about his weight, decides to weigh himself in an elevator. He stands on a bathroom scale in an elevator moving upward at speed v. As the elevator reaches his floor, it slows to a stop over a distance, d. Determine the reading on the bathroom scale (Fscale) as a function of m, v, d, and g.
Motion Diagram Motion Information Free-Body Diagram
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
|
Mathematical Analysis
Questions
If v = 0 m/s, what should Fscale equal? Does your function agree with this observation?
If d = ∞, what should Fscale equal? Does your function agree with this observation?
For what stopping distance, d, would the bathroom scale read 0 N? Would the scale also read 0 N for this stopping distance if the elevator was initially moving downward?
A falling pole-vaulter of mass m lands on a cushion at speed v. The pole-vaulter sinks a distance d into the cushion before stopping. Determine the force exerted on the pole-vaulter due to the cushion (Fcushion) as a function of m, v, d, and g.
Motion Diagram Motion Information Free-Body Diagram
 | Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
|
Mathematical Analysis
Questions
If v = 0 m/s, what should Fcushion equal? Does your function agree with this observation?
If d = 0 m, what should Fcushion equal? Does your function agree with this observation?
What would be worse for the pole-vaulter, hitting the cushion at twice her original speed or sinking half of the original distance into the cushion?
A pole-vaulter of mass m falls off a wall a distance D above a cushion. The pole-vaulter sinks a distance d into the cushion before stopping. Determine the force exerted on the pole-vaulter due to the cushion (Fcushion) as a function of m, D, d, and g.
Motion Diagram Motion Information Free-Body Diagrams
|
| Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3:
t3 = r3 = v3 =
| before hitting cushion
after hitting cushion |
Mathematical Analysis
Questions
If D = ∞, what should Fcushion equal? Does your function agree with this observation?
If d = 0 m, what should Fcushion equal? Does your function agree with this observation?
What would be worse for the pole-vaulter, starting at twice the initial distance above the cushion or sinking half of the original distance into the cushion?
Tired of walking up the stairs, an engineering student of mass m designs an ingenious device for reaching his third floor dorm room. A block of mass M is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room in a time T. Determine the velocity of the student (v) when he reaches his room as a function of m, M, T and g.
Motion Diagram Motion Information Free-Body Diagrams
 | Object: Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 =
| student | block
|
Mathematical Analysis
Questions
If g = 0 m/s2, what should v equal? Does your function agree with this observation?
If m = M, what should v equal? Does your function agree with this observation?
If M = ∞, what should v equal? Does your function agree with this observation?
A rocket of mass m is fired vertically upward from rest. The rocket’s engine produces a thrust of constant magnitude Fthrust for tthrust seconds. Determine the maximum height reached by the rocket (H) as a function of Fthrust, tthrust, m, and g.
Motion Information Free-Body Diagrams
| Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3:
t3 = r3 = v3 =
| before engine turns off | after engine turns off |
Mathematical Analysis
Questions
If g = 0 m/s2, what should H equal? Does your function agree with this observation?
If Fthrust = mg, what should H equal? Does your function agree with this observation?
A rocket of mass m is fired vertically upward from rest. The rocket’s engine produces a thrust of constant magnitude Fthrust for tthrust seconds. Determine the time it takes the rocket to reach its apex (tapex) as a function of Fthrust, tthrust, m, and g.
Motion Information Free-Body Diagrams
| Event 1:
t1 = r1 = v1 = a12 = | Event 2:
t2 = r2 = v2 = a23 = | Event 3:
t3 = r3 = v3 =
| before engine turns off | after engine turns off |
Mathematical Analysis
Questions
If g = 0 m/s2, what should tapex equal? Does your function agree with this observation?
If Fthrust = mg, what should tapex equal? Does your function agree with this observation?
[1] When the only force acting on an object is the force of gravity, the situation is termed freefall.
[i] F rope = 420 N
[ii] F cushion = 1910 N
[iii] a ≥ 4.49 m/s2
[iv] t2 = 17.1 s to reach ground
[v] F cushion = 2830 N
[vi] F ground = 43700 N
[vii] r3 = 63.5 m
[viii] r3 = 1550 m
[ix] m block = 240 kg
[x] m block = 26 kg
[xi] F rope = 500 N
[xii] F rope = 466 N
http://www.compadre.org/IVV/vignettes/newtonsFirstLaw.cfm
http://www.compadre.org/IVV/vignettes/newtonsSecondLaw.cfm
http://www.compadre.org/IVV/vignettes/newtonsThirdLaw.cfm
Homework 2 – Model 1: 74, 77, 78, 81, 82, 90, 95, 96, 97, and 102.
- University Physics I Homework Assignments. Authored by: Mary Mohr. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike