8.2: Conservative Interactions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Let's summarize the physical concepts and principles we have encountered so far in our study of classical mechanics. We have “discovered” one important quantity, the inertia or inertial mass of an object, and introduced two different quantities based on that concept, the momentum m→v and the kinetic energy 12mv2. We found that these quantities have different but equally intriguing properties. The total momentum of a system is insensitive to the interactions between the parts that make up the system, and therefore it stays constant in the absence of external influences (a more general statement of the law of inertia, the first important principle we encountered). The total kinetic energy, on the other hand, changes while any sort of interaction is taking place, but in some cases it may actually return to its original value afterwards. This chapter deals with interactions from an energy point of view, whereas later chapters will deal with them from a force point of view.
In the previous chapter I suggested that what was going on in an elastic collision could be interpreted, or described (perhaps in a figurative way) more or less as follows: as the objects come together, the total kinetic energy goes down, but it is as if it was being temporarily stored away somewhere, and as the objects separate, that “stored energy” is fully recovered as kinetic energy. Whether this does happen or not in any particular collision (that is, whether the collision is elastic or not) depends, as we have seen, on the kind of interaction (“bouncy” or “sticky,” for instance) that takes place between the objects.
We are going to take the above description literally, and use the name conservative interaction for any interaction that can “store and restore” kinetic energy in this way. The “stored energy” itself—which is not actually kinetic energy while it remains stored, since it is not given by the value of 12mv2 at that time—we are going to call potential energy. Thus, conservative interactions will be those that have a “potential energy” associated with them, and vice-versa.
Potential Energy
Perhaps the simplest and clearest example of the storage and recovery of kinetic energy is what happens when you throw an object straight upwards, as it rises and eventually falls back down. The object leaves your hand with some kinetic energy; as it rises it slows down, so its kinetic energy goes down, down... all the way down to zero, eventually, as it momentarily stops at the top of its rise. Then it comes down, and its kinetic energy starts to increase again, until eventually, as it comes back to your hand, it has very nearly the same kinetic energy it started out with (exactly the same, actually, if you neglect air resistance).
The interaction responsible for this change in the object’s kinetic energy is, of course, the gravitational interaction between it and the Earth, so we are going to say that the “missing” kinetic energy is temporarily stored as gravitational potential energy of the system formed by the Earth and the object. This potential energy takes a simple mathematical form,
Ug=mgy,
where y is the height of the object above the Earth. We have carefully called this height the coordinate y to emphasize that is can be negative if y is negative. It turns out that with this definition of potential energy, the total energy in freefall is
K+UG=constant.
This is a statement of conservation of energy under the gravitational interaction. For any interaction that has a potential energy associated with it, the quantity K+U is called the (total) mechanical energy.
Figure 8.2.1 shows how the kinetic and potential energies of an object thrown straight up change with time (don't worry where this plot comes from yet, you will learn about that when we study projectile motion in detail). I have arbitrarily assumed that the object has a mass of 1 kg and an initial velocity of 2 m/s, and it is thrown from an initial height of 0.5 m above the ground. Note how the change in potential energy exactly mirrors the change in kinetic energy (so ΔUG=−ΔK, mathematically), and the total mechanical energy remains equal to its initial value of 6.9 J throughout.
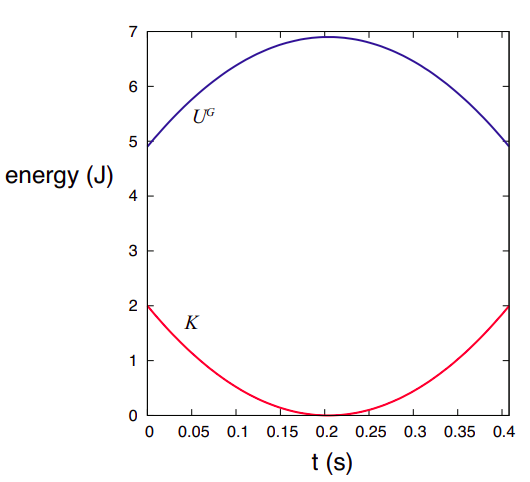
There is something about potential energy that probably needs to be mentioned at this point. Because I have chosen to launch the object from 0.5 m above the ground, and I have chosen to measure y from the ground, I started out with a potential energy of mgyi = 4.9 J. This makes sense, in a way: it tells you that if you simply dropped the object from this height, it would have picked up an amount of kinetic energy equal to 4.9 J by the time it reached the ground. But, actually, where I choose the vertical origin of coordinates is arbitrary. I could start measuring y from any height I wanted to—for instance, taking the initial height of my hand to correspond to y = 0. This would shift the blue curve in Figure 8.2.1 down by 4.9 J, but it would not change any of the physics. The only important thing I really want the potential energy for is to calculate the kinetic energy the object will lose or gain as it moves from one height to another, and for that only changes in potential energy matter. I can always add or subtract any (constant) number to or from U, and it will still be true that ΔK=−ΔU.
Closed Systems
Today, physics is pretty much founded on the belief that the energy of a closed system (defined as one that does not exchange energy with its surroundings—more on this in a minute) is always conserved: that is, internal processes and interactions will only cause energy to be “converted” from one form into another, but the total, after all the forms of energy available to the system have been carefully accounted for, will not change. This belief is based on countless experiments, on the one hand, and, on the other, on the fact that all the fundamental interactions that we are aware of do conserve a system’s total energy.
Of course, recognizing whether a system is “closed” or not depends on having first a complete catalogue of all the ways in which energy can be stored and exchanged—to make sure that there is, in fact, no exchange of energy going on with the surroundings. Note, incidentally, that a “closed” system is not necessarily the same thing as an “isolated” system: the former relates to the total energy, the latter to the total momentum. A parked car getting hotter in the sun is not a closed system (it is absorbing energy all the time) but, as far as its total momentum is concerned, it is certainly fair to call it “isolated.” Hopefully all these concepts will be further clarified when we introduce the additional auxiliary concepts of force, work, and heat.
For a closed system, we can state the principle of conservation of energy (somewhat symbolically) in the form
where K is the total, macroscopic, kinetic energy; U the sum of all the applicable potential energies associated with the system’s internal interactions; Esource is any kind of internal energy (such as chemical energy) that is not described by a potential energy function, but can increase the system’s mechanical energy; and Ediss stands for the contents of the “dissipated energy reservoir”—typically thermal energy. As with the potential energy U, the absolute value of Esource and Ediss does not (usually) really matter: all we are interested in is how much they change in the course of the process under consideration.
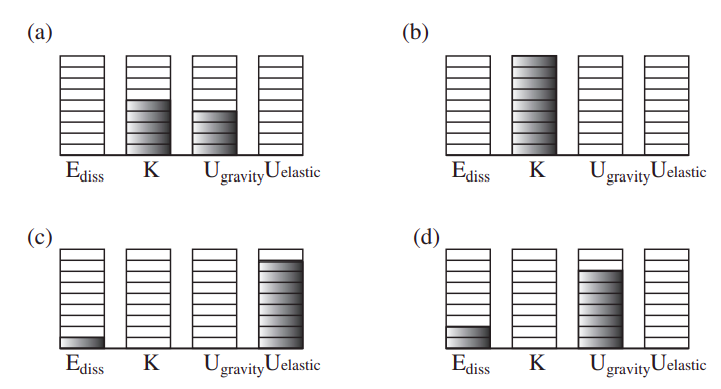
Figure 8.2.1 above is an example of this kind of “energy accounting” for a ball bouncing on the ground. If the ball is thrown down, the system formed by the ball and the earth initially has both gravitational potential energy, and kinetic energy (diagram (a)). So all the kinetic energy that we have is the kinetic energy of the ball. As the ball falls, gravitational potential energy is being converted into kinetic energy, and the ball speeds up. As it is about to hit the ground (diagram (b)), the potential energy is zero and the kinetic energy is maximum. During the collision with the ground, all the kinetic energy is temporarily converted into other forms of energy, which are essentially elastic energy of deformation (like the energy in a spring) and some thermal energy (diagram (c)). When it bounces back, its kinetic energy will only be a fraction e2 of what it had before the collision (where e is the coefficient of restitution). This kinetic energy is all converted into gravitational potential energy as the ball reaches the top of its bounce (diagram (d)). Note there is more dissipated energy in diagram (d) than in (c); this is because I have assumed that dissipation of energy takes place both during the compression and the subsequent expansion of the ball.
Note that in this closed system, some energy was transferred to heat, but the total energy stayed the same, and was therefore conserved. The real problem appears if you can't actually keep track of that energy that gets transferred to heat, then the system would appear not to conserve energy. Mostly, we will assume no transfer to heat in our problems, but we should acknowledge this is not a problem with physics, it is rather a problem with our ability to keep track of all the sources of energy in a system. As you move through the field of physics, you will learn how we keep track of more of these sources of energy, and the problems you solve will become better and better approximations to "the real world".


