11.2: Rolling Motion

When considering objects that can move both translationally (up, down, left, right, in, out!) and rotationally, we are immediately confronted with a problem: these two motions can be either completely independent, completely related to each other, or something even in-between. Take for example a baseball thrown by a pitcher. It follows a particular path from the mound to the plate (its translational motion), but it might also have some spin (it's rotational motion). Those seem pretty independent, but in fact spinning balls like that can swerve back in forth because of something called The Magnus Effect (check it out on Wikipedia). Of course, that's why pitchers make the ball do that, is that motion makes it more complicated for the batter to hit the ball. The problem is that coupling between the air and the ball is weak in some sense - most of the energy of the ball is used for it's forward motion, only a small amount is used to make the ball move back and forth through the air.

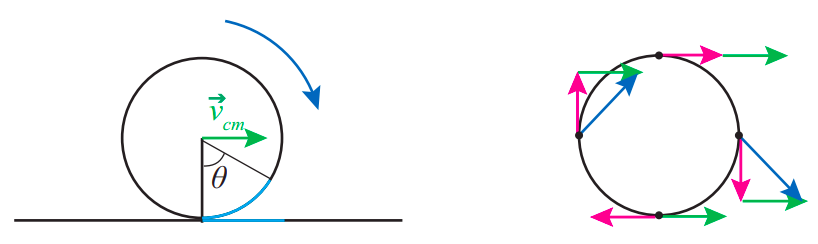
Naturally, we would like to understand those kinds of interesting situations, but they end up being rather complicated. We would like to start with something simpler - motion in which the translation and rotation are either completely independent, and can be solved completely separately, or they are easily related to each other. If they are independent, you can solve them based on what you know already! However, there is a case in which the motions are completely related to each other, and is very common, called rolling without slipping. In this case, the translational motion and the rotational motion are coupled, and the relevant velocities are related to each other:

\[ | \vec v_{cm} | = R |\omega| \label{eq:9.34} .\]

Here \(R\) is the radius of the entire object. Notice how this expression relates to Equation (6.1.1) from a previous section - they look very similar, but they are actually saying two somewhat different things. Equation (6.1.1) told us the relationship between the angular and linear speed of a particular point on an object, while the expression above tells us how to related the angular and linear speed of the entire object (remember that the center of mass is the location at which the object is, if the object was a single point).

The origin of the condition (\ref{eq:9.34}) is fairly straightforward. You can imagine an object that is rolling without slipping as “measuring the surface” as it rolls (or vice-versa, the surface measuring the circumference of the object as its different points are pressed against it in succession). So, after it has completed exactly one revolution (\(2\pi\) radians), it should have literally “covered” a distance on the surface equal to \(2\pi R\), that is, advanced a distance \(2\pi R\). But the same has to be true, proportionately, for any rotation angle \(\Delta \theta\) other that \(2\pi\): since the length of the corresponding arc is \(s = R|\Delta \theta|\), in a rotation over an angle \(|\Delta \theta|\) the center of mass of the object must have advanced a distance \(|\Delta x_{cm}| = s = R|\Delta \theta|\). Dividing by \(\Delta t\) as \(\Delta t \rightarrow 0\) then yields Equation (\ref{eq:9.34}).

Figure \(\PageIndex{1}\): Left: illustrating the rolling without slipping condition. The cyan line on the surface has the same length as the cyan-colored arc, and will be the distance traveled by the disk when it has turned through an angle \(\theta\). Right: velocities for four points on the edge of the disk. The pink arrows are the velocities in the center of mass frame. In the Earth reference frame, the velocity of the center of mass, \(\vec v_{cm}\), in green, has to be added to each of them. The resultant is shown in blue for two of them.

Considering a single rolling objects, the total kinetic energy can now be written as two terms,

\[K=K_{rot}+K_{cm}=\frac{1}{2}I\omega^2 +\frac{1}{2}mv_{cm}^2\]

combining this with the condition of rolling without slipping (\ref{eq:9.34}), we see that the ratio of the translational to the rotational kinetic energy is

\[ \frac{K_{c m}}{K_{r o t}}=\frac{m v_{c m}^{2}}{I \omega^{2}}=\frac{m R^{2}}{I} \label{eq:9.43} .\]

The amount of energy available to interact with the object is whatever potential energy is running around the system, and that has to be split between translational and rotational in the proportion (\ref{eq:9.43}). An object with a proportionately larger \(I\) is one that, for a given angular velocity, needs more rotational kinetic energy, because more of its mass is away from the rotation axis. This leaves less energy available for its translational motion.