12.2: Examples

Whiteboard Problem \(\PageIndex{1}\): Croquet Collision

                                 

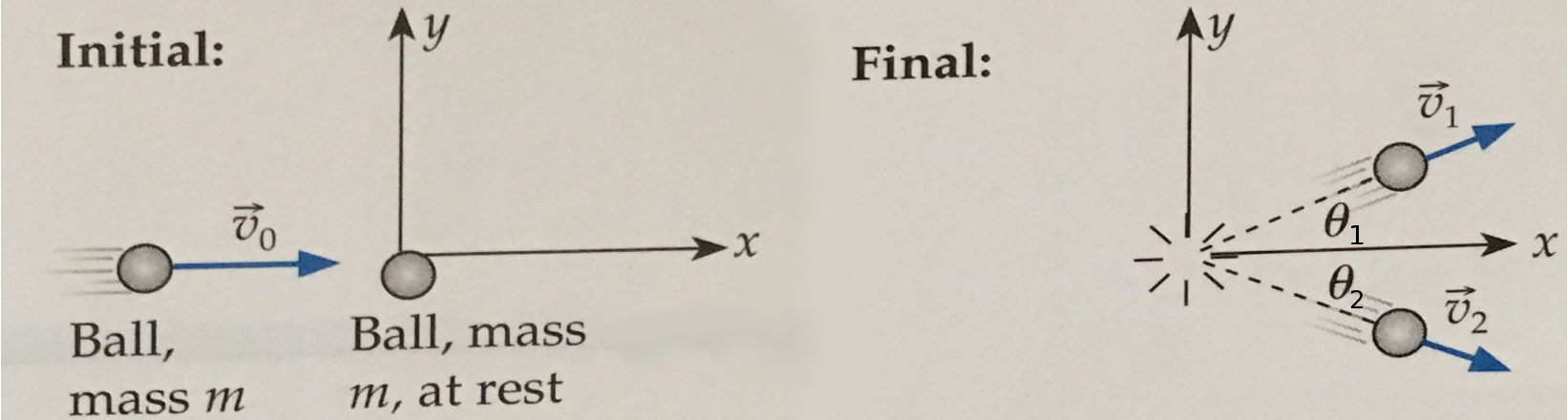
A Croquet player hits a wooden croquet ball, of mass \(m=0.450\) kg,  at a speed of \(v_0=3.5\) m/s, which collides, off-center, with a stationary ball of the same mass. After the collision, the first ball moves off with a speed of \(v_1=3.0\) m/s at an angle of \(\theta_1=10^{\circ}\) with respect to the x-axis, as shown in the figure. You may assume that this collision is inelastic.

1. At what angle, \(\theta_2\), relative to the x-axis does the second ball move away from the collision at?
2. What is the final speed of the second ball, \(v_2\)?
3. What was the change in energy of this collision? Can you explain your answer?

 

Whiteboard Problem \(\PageIndex{2}\): Pool Shark

A billiard ball moving at 3.06 m/s strikes a second billiard ball, of the same mass (150 g) and initially at rest, in a perfectly elastic collision. After the collision, the first ball moves away with a speed 2.65 m/s. 

1. What is the initial kinetic energy of the system?
2. What is the final speed of the second ball?
3. If the first ball leaves the collision at an angle of 30\(^\circ\) with respect to the original direction of motion, what angle does the second ball leave the collision at?

 

Whiteboard Problem \(\PageIndex{3}\): Red Light!

I am responsibly driving my 1360-kg Subaru Impreza through an intersection. I am traveling west, my light is green, so I proceed through at 45 mph. An irresponsible driver in a brand new Audi R8 (of mass 1678 kg) with Florida plates blows through the red light going north. He smashes into me, and our cars stick together after the collision, traveling at an angle of 65\(^\circ\) north of west. 

1. Determine both (which can be done in either order),
   1. How fast was he traveling before he hit me?
   2. How fast are the two cars moving together after the collision?
2. What fraction of the total energy of the system was lost during this collision?

 

Whiteboard Problem \(\PageIndex{4}\): The Space Goo:

You are flying through empty space in your rocket, at 2000 m/s, far away from any stars, planets, or other massive bodies. However, you aren't paying very careful attention so you don't notice that there is a giant cube of ``Space-goo'' on a collision course with you! It is moving at a speed of 500 m/s in a direction perpendicular to your own, and has a mass of 3000 kg.

Assuming the total mass of you and your personal rocket is 1500 kg, and you get stuck in the space-goo when you collide, what is the magnitude and direction of your final velocity after the collision?

Example \(\PageIndex{5}\): Collision Graph revisited

Look again at the collision graph from Example 2.4.1 from the point of view of the kinetic energy of the two carts.

1. What is the initial kinetic energy of the system?
2. How much of this is in the center of mass motion, and how much of is convertible?
3. Does the convertible kinetic energy go to zero at some point during the collision? If so, when? Is it fully recovered after the collision is over?
4. What kind of collision is this? (Elastic, inelastic, etc.) What is the coefficient of restitution?

Solution

(a) From the solution to Example 3.5.1 we know that

\begin{aligned}
v_{1 i}=&-1 \: \frac{\mathrm{m}}{\mathrm{s}} & & v_{2 i}=0.5 \: \frac{\mathrm{m}}{\mathrm{s}} \\
v_{1 f}=&1 \: \frac{\mathrm{m}}{\mathrm{s}} & & v_{2 f}=-0.5 \: \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}

and \(m_1\) = 1 kg and \(m_2\) = 2 kg. So the initial kinetic energy is

\[ K_{s y s, i}=\frac{1}{2} m_{1} v_{1 i}^{2}+\frac{1}{2} m_{2} v_{2 i}^{2}=0.5 \: \mathrm{J}+0.25 \: \mathrm{J}=0.75 \: \mathrm{J} \label{eq:4.17} \]

(b) To calculate \(K_{cm} = \frac{1}{2} (m_1 + m_2)v^2_{cm}\), we need \(v_{cm}\), which in this case is equal to

\[ v_{c m}=\frac{m_{1} v_{1 i}+m_{2} v_{2 i}}{m_{1}+m_{2}}=\frac{-1+2 \times 0.5}{3}=0 \nonumber \]

so \(K_{cm}\) = 0, which means all the kinetic energy is convertible. We can also calculate that directly:

\[ K_{\text {conv}, i}=\frac{1}{2} \mu v_{12, i}^{2}=\frac{1}{2}\left(\frac{1 \times 2}{1+2} \: \mathrm{kg}\right) \times\left(0.5 \: \frac{\mathrm{m}}{\mathrm{s}}-(-1) \: \frac{\mathrm{m}}{\mathrm{s}}\right)^{2}=\frac{1.5^{2}}{3} \: \mathrm{J}=0.75 \: \mathrm{J} \label{eq:4.18} \]

(c) If we look at figure 2.4.1, we can see that the carts do not pass through each other, so their relative velocity must be zero at some point, and with that, the convertible energy. In fact, the figure makes it quite clear that both \(v_1\) and \(v_2\) are zero at \(t\) = 5 s, so at that point also \(v_{12}\) = 0, and the convertible energy \(K_{conv}\) = 0. (And so is the total \(K_{sys}\) = 0 at that time, since \(K_{cm}\) = 0 throughout.)

On the other hand, it is also clear that \(K_{conv}\) is fully recovered after the collision is over, since the relative velocity just changes sign:

\begin{array}{l}
{v_{12, i}=v_{2 i}-v_{1 i}=0.5 \: \frac{\mathrm{m}}{\mathrm{s}}-(-1) \: \frac{\mathrm{m}}{\mathrm{s}}=1.5 \: \frac{\mathrm{m}}{\mathrm{s}}} \\
{v_{12, f}=v_{2 f}-v_{1 f}=-0.5 \: \frac{\mathrm{m}}{\mathrm{s}}-1 \: \frac{\mathrm{m}}{\mathrm{s}}=-1.5 \: \frac{\mathrm{m}}{\mathrm{s}}} \label{eq:4.19}
\end{array}

Therefore

\[ K_{\text {conv}, f}=\frac{1}{2} \mu v_{12, f}^{2}=\frac{1}{2} \mu v_{12, i}^{2}=K_{\text {conv}, i} \nonumber \]

(d) Since the total kinetic energy (which in this case is only convertible energy) is fully recovered when the collision is over, the collision is elastic. Using equation (\ref{eq:4.19}), we can see that the coefficient of restitution is

\[ e=-\frac{v_{12, f}}{v_{12, i}}=-\frac{-1.5}{1.5}=1 \nonumber \]

as it should be.