15.5: Examples

 

Whiteboard Problem \(\PageIndex{1}\): Ski Jump!

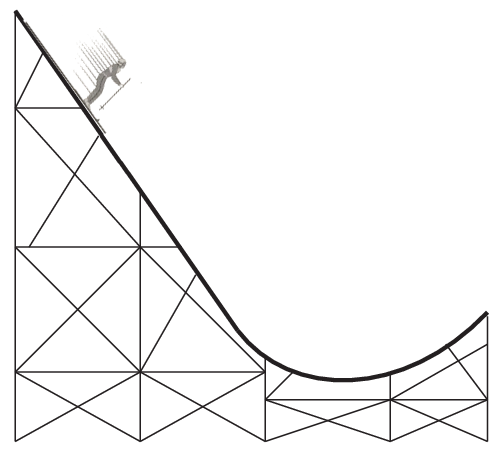
Consider the ski jumper in the above figure. The mass of the skiier is 75 kg, and the slope down which he is traveling is 37\(^\circ\) with respect to the horizontal (which is a typical ``in-run'' to an olympic ski jump).

1. What is the normal force on this skiier, while they are traveling down the slope as shown in the figure?
2. Assuming the snow is perfectly frictionless, what is the acceleration of the skier?
3. How long will it take the skiier to go from the top of the slope to the bottom, if the slope is 115 m long? You may assume they started from rest.
4. How fast will the skiier be moving at the end of this slope?

Whiteboard Problem \(\PageIndex{2}\): Average and Instantaneous Velocity

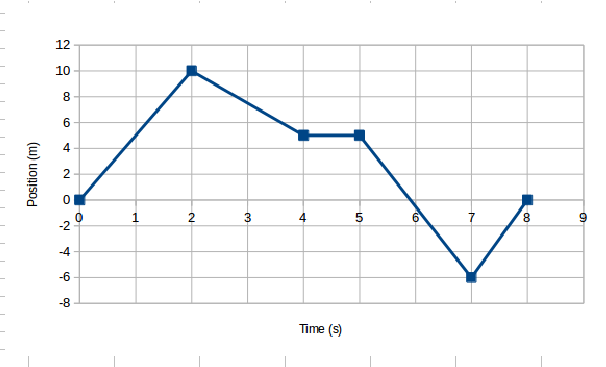
Consider the graph of position vs time in the figure.

1. Find the average velocity during the time intervals 0 s to 2 s, 2 s to 5 s, and 5 s to 7 s.
2. Find the instantaneous velocity at 1 s, 4.5 s, and 7.5 s.

 

Whiteboard Problem \(\PageIndex{3}\): The Tortoise and the Hare, Redux!

The tortoise demands a rematch! They decide on the same distance (\(d\) = 1.0 km), and the tortoise starts off at his same speed (\(v_t\) = 0.20 m/s). This time, the hare is so convinced he will win that he waits at the start for the tortoise to get to \(d_1\) = 0.80 km before he starts to run (hop?), starting from rest at a constant acceleration.

1. What acceleration will the hare need to have to finish the race at the same time as the tortoise?
2. The tortoise expects this kind of grandstanding from the hare, so he begins to accelerate at 0.01 m/s\(^2\) when he sees the hare start the race. What acceleration must the hare have to still beat the tortoise?

Example \(\PageIndex{4}\): Motion with piecewise constant acceleration

Construct the position vs. time, velocity vs. time, and acceleration vs. time graphs for the motion described below. For each of the intervals (a)–(d) you’ll need to figure out the position (height) and velocity of the rocket at the beginning and the end of the interval, and the acceleration for the interval. In addition, for interval (b) you need to figure out the maximum height reached by the rocket and the time at which it occurs. For interval (d) you need to figure out its duration, that is to say, the time at which the rocket hits the ground.

1. A rocket is shot upwards, accelerating from rest to a final velocity of 20 m/s in 1 s as it burns its fuel. (Treat the acceleration as constant during this interval.)
2. From \(t\) = 1 s to \(t\) = 4 s, with the fuel exhausted, the rocket flies under the influence of gravity alone. At some point during this time interval (you need to figure out when!) it stops climbing and starts falling.
3. At \(t\) = 4 s a parachute opens, suddenly causing an upwards acceleration (again, treat it as constant) lasting 1 s; at the end of this interval, the rocket’s velocity is 5 m/s downwards.
4. The last part of the motion, with the parachute deployed, is with constant velocity of 5 m/s downwards until the rocket hits the ground.

Solution

(a) For this first interval (for which I will use a subscript “1” throughout) we have

\[ \Delta y_{1}=\frac{1}{2} a_{1}\left(\Delta t_{1}\right)^{2} \label{eq:2.18} \]

using Equation (15.2.7) for motion with constant acceleration with zero initial velocity (I am using the variable \(y\), instead of \(x\), for the vertical coordinate; this is more or less customary, but, of course, I could have used \(x\) just as well).

Since the acceleration is constant, it is equal to its average value:

\[ a_{1}=\frac{\Delta v}{\Delta t}=20 \: \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber .\]

Substituting this into (\ref{eq:2.18}) we get the height at \(t\) = 1 s is 10 m. The velocity at that time, of course, is \(v_{f1}\) = 20 m/s, as we were told in the statement of the problem.

(b) This part is free fall with initial velocity \(v_{i2}\) = 20 m/s. To find how high the rocket climbs, use Equation (15.3.1) in the form \(v_{top} − v_{i2} = −g(t_{top} − t_{i2})\), with \(v_{top} = 0\) (as the rocket climbs, its velocity decreases, and it stops climbing when its velocity is zero). This gives us \(t_{top}\) = 3.04 s as the time at which the rocket reaches the top of its trajectory, and then starts coming down. The corresponding displacement is, by Equation (15.3.2),

\[ \Delta y_{t o p}=v_{i 2}\left(t_{t o p}-t_{i 2}\right)-\frac{1}{2} g\left(t_{t o p}-t_{i 2}\right)^{2}=20.4 \: \mathrm{m} \nonumber \]

so the maximum height it reaches is 30.4 m.

At the end of the full 3-second interval, the rocket’s displacement is

\[ \Delta y_{2}=v_{i 2} \Delta t_{2}-\frac{1}{2} g\left(\Delta t_{2}\right)^{2}=15.9 \: \mathrm{m} \nonumber \]

(so its height is 25.9 m above the ground), and the final velocity is

\[ v_{f 2}=v_{i 2}-g \Delta t_{2}=-9.43 \: \frac{\mathrm{m}}{\mathrm{s}} \nonumber .\]

(c) The acceleration for this part is \((v_{f3} −v_{i3})/ \Delta t_3\) = (−5 + 9.43)/1=4.43 m/s². Note the positive sign. The displacement is

\[ \Delta y_{3}=-9.43 \times 1+\frac{1}{2} \times 4.43 \times 1^{2}=-7.22 \: \mathrm{m} \nonumber \]

so the final height is 25.9 − 7.21 = 18.7 m.

(d) This is just motion with constant speed to cover 18.7 m at 5 m/s. The time it takes is 3.74 s. The graphs for this motion are shown earlier in the chapter, in Figure 15.2.3.