16.3: Inclined Planes

Another simple example of 2D motion is a block sliding down a plane. Now in this case, the block is not actually moving in 2D motion, since it's just moving in a straight line down the plane, but the forces are acting in 2 dimensions, which is what we have to understand to understand the motion. So here we will consider an inclined plane making an angle $\theta$ with the horizontal was $g \sin \theta$. This problem is going to introduce two kinds of friction as well, kinetic friction $F_k$, which you get when an object is in motion, and static friction $F_s$, which you get when an object is stuck in place. We will study friction more in Chapter 18 - for now just use your intuition about friction "slowing objects down", and "preventing them from moving".

Figure $\PageIndex{1}$: A block sliding down an inclined plane. The corresponding free-body diagram is shown on the right.

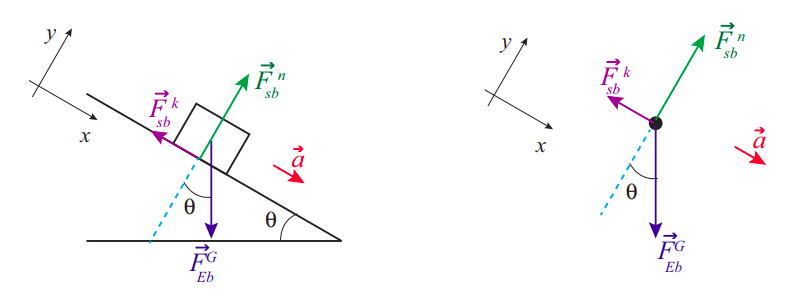
Figure $\PageIndex{1}$ above shows, on the left, a block sliding down an inclined plane and all the forces acting on it. These are more clearly seen on the free-body diagram on the right. I have labeled all the forces using the $\vec{F}_{b y, o n}^{t y p e}$ convention introduced back in 14.1 (so, for instance, $\vec{F}_{sb}^{k}$ is the force of kinetic friction exerted by the surface on the block); however, later on, for algebraic manipulations, and especially where $x$ and $y$ components need to be taken, I will drop the “by, on” subscripts, and just let the “type” superscript identify the force in question.

The diagrams also show the coordinate axes I have chosen: the $x$ axis is along the plane, and the $y$ is perpendicular to it. The advantage of this choice is obvious: the motion is entirely along one of the axes, and two of the forces (the normal force and the friction) already lie along the axes. The only force that does not is the block’s weight (that is, the force of gravity), so we need to decompose it into its $x$ and $y$ components. For this, we can make use of the fact, which follows from basic geometry, that the angle of the incline, $\theta$, is also the angle between the vector $\vec F^g$ and the negative $y$ axis. This means we have

$$\begin{align} &F_{x}^{g}=F^{g} \sin \theta \nonumber \\ &F_{y}^{g}=-F^{g} \cos \theta \label{eq:8.14}. \end{align}$$

Equations ($\ref{eq:8.14}$) also show another convention I will adopt from now, namely, that whenever the symbol for a vector is shown without an arrow on top or an $x$ or $y$ subscript, it will be understood to refer to the magnitude of the vector, which is always a positive number by definition.

Newton’s second law, as given by equations (16.1.2) applied to this system, then reads:

$$F_{x}^{g}+F_{x}^{k}=m a_{x}=F^{g} \sin \theta-F^{k} \label{eq:8.15}$$

for the motion along the plane, and

$$F_{y}^{g}+F_{y}^{n}=m a_{y}=-F^{g} \cos \theta+F^{n} \label{eq:8.16}$$

for the direction perpendicular to the plane. Of course, since there is no motion in this direction, $a_y$ is zero. This gives us immediately the value of the normal force:

$$F^{n}=F^{g} \cos \theta=m g \cos \theta \label{eq:8.17}$$

since $F^g = mg$. Now including our force of kinetic friction $F_k$, along with $F^G = mg$ in Equation ($\ref{eq:8.15}$), we get

$$m a_{x}=m g \sin \theta-F_k \label{eq:8.19} .$$

We can eliminate the mass to obtain finally

$$a_{x}=g\left(\sin \theta-\frac{F_k}{m}\right) \label{eq:8.20}$$

which is the desired result. In the absence of friction ($\mu_k$ = 0) this gives $a = g \sin \theta$, a result you might have seen already.

Of course, we know from experience that what happens when $\theta$ is very small is that the block does not slide: it is held in place by the force of static friction. The diagram for such a situation looks the same as Figure $\PageIndex{1}$, except that $\vec a$ = 0, the force of friction is $F^s$ instead of $F^k$, and of course its magnitude must match that of the $x$ component of gravity. Equation ($\ref{eq:8.15}$) then becomes

$$m a_{x}=0=F^{g} \sin \theta-F^{s} \label{eq:8.21} .$$

It turns out that the force of static friction $F_s$ does not have a fixed value - it just has a maximum value, over which the object starts to move. In this case we can find this maximum value by looking at the previous equation; as long as the static friction obeys

$$F_s \leq F^g \sin\theta,$$

the block will remain stationary. Again, we will look at this result more carefully in Chapter 18.

What if we send the block sliding up the plane instead? The acceleration would still be pointing down (since the object would be slowing down all the while), but now the force of kinetic friction would point in the direction opposite that indicated in Figure $\PageIndex{1}$, since it always must oppose the motion. If you go through the same analysis I carried out above, you will get that $a_x = g (\sin \theta + F_k)$ in that case, since now friction and gravity are working together to slow the motion down.