19.2: Springs

Last updated
Save as PDF

Page ID: 63270

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

From Wikipedia: A spring is an elastic object that stores mechanical energy. Although real springs can be rather complicated, in physics we normally deal with idealized springs, which can be modeled relatively easily. In addition, this model is widely applicable for many other physical interactions, like between molecules or other fundamental particles. In fact, nearly every interaction in the universe looks like a spring if you consider just small displacements from equilibrium positions. In this section we will carefully outline how to model the interaction of a spring using forces - the chapter on potential energy has already discussed modeling the spring as an energy storage device.

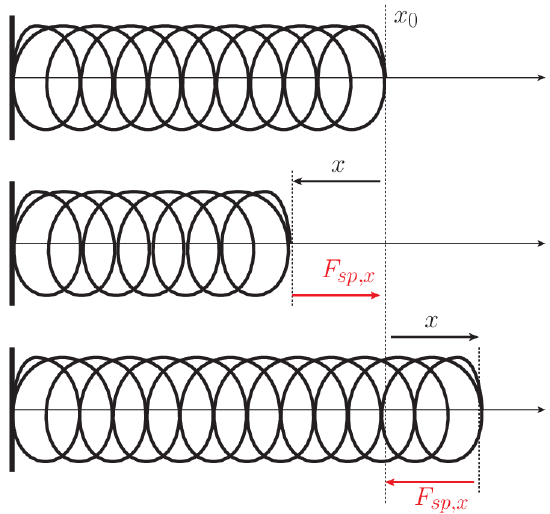
A spring has an equilibrium position (see the figure above), at which it will stay until forces are applied to it. If we use a coordinate system with the origin at the fixed end of the spring, we will call this equilbrium position \(x_0\). When the end of the spring is moved to a different location \(x\), the response force from the spring is linear in the displacement \(x-x_0|\), with a constant of proportionality \(k\) (the spring constant). This constant of proportionality is different for every spring, but remains constant during all interactions. The basic observation of linear proportionality is the content of Hooke's Law.

There are several equivalent ways of representing the force mathematically. Using the quantities defined above, we can write the magnitude as simply

\[|F_{sp}|=k|x-x_0|.\]

Of course, this doesn't take into account the direction of the force, only the size. Since the direction of the force is opposite of the displacement (compressed springs push against the compression, whereas stretched springs pull back - this is why the spring force is often called a restoring force), we need to be a little careful to get that right. One way to do this is to write the component of the force along the displacement as

\[F_{sp,x}=-k(x-x_0).\]

Notice the signs of the various quantities (the overall negative sign in particular) in comparison to the figure above. When the spring is stretched, we have \(x>x_0\) so \(x-x_0\) is positive, and the overall force is in the negative-x direction, as expected. When the spring is compressed, \(x<x_0\) so \(x-x_0\) is negative, but the overall negative sign ensures the force is now in the positive direction, as expected.

Generally, this is the most useful way to write the spring force. However, it is sometimes advantageous to set the equilibrium position of the spring as the origin of the coordinate system, \(x_0=0\). In this case, the spring force is simply

\[F_{sp,x}=-kx.\]

You can check yourself that the signs work out the same way as they did in the other expression.

It's also possible to write this force as a vector, but we have to be a bit more careful. In cases where the idealized spring model is expected to be valid, one can write

\[\vec{F}_{sp}=-k(\vec{r}-\vec{r}_0),\]

where \(\vec{r}_0\) is the equilibrium position of the end of the spring, and \(\vec{r}\) is the current position. However, this might start falling apart when considering various aspects of "real" springs. For example, if the end of the spring is allowed to rotate, the spring could find other equilbrium positions at distances \(|r_0|\) from the origin, but at a different location than the original position. These can all be dealt with, so long as we understand how to apply the basic model of Hooke's law.