21.1: Forces and Potential Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider the special case of two interacting objects, in which a lighter object is interacting with a much more massive one, so that the massive one essentially does not move at all as a result of the interaction. Note that this does not contradict Newton’s 3rd law, Equation (6.1.5): the forces the two objects exert on each other are the same in magnitude, but the acceleration of each object is inversely proportional to its mass, so F12=−F21 implies
m2a2=−m1a1
and so if, for instance, m2≫m1, we get |a2|=|a1|m1/m2≪|a1|. In words, the more massive object is less responsive than the less massive one to a force of the same magnitude. This is just how we came up with the concept of inertial mass in the first place!
Anyway, in this situation we could just write the potential energy function of the whole system as a function of only the lighter object’s coordinate, U(x). Let's use this simplified setup to demonstrate a very interesting relationship between potential energies and forces. Suppose this is a closed system in which no dissipation of energy is taking place. Then the total mechanical energy is a constant:
Emech=12mv2+U(x)= constant
(Here, m is the mass of the lighter object, and v its velocity; the more massive object does not contribute to the total kinetic energy, since it does not move!)
As the lighter object moves, both x and v in Equation (???) change with time. So I can take the derivative of Equation (???) with respect to time, using the chain rule, and noting that, since the whole thing is a constant, the total value of the derivative must be zero:
0=ddt(12m(v(t))2+U(x(t)))=mv(t)dvdt+dUdxdxdt.
But note that dx/dt is just the same as v(t). So I can cancel that on both terms, and then I am left with
mdvdt=−dUdx.
But dv/dt is just the acceleration a, and F=ma. So this tells me that
F=−dUdx
and this is how you can always get the force from a potential energy function.
Let us check it right away for the force of gravity: we know that UG=mgy, so
FG=−dUGdy=−ddy(mgy)=−mg.
Is this right? It seems to be! Recall all objects fall with the same acceleration, −g (assuming the upwards direction to be positive), so if F=ma, we must have FG=−mg. So the gravitational force exerted by the earth on any object (which I would denote in full by FGE,o) is proportional to the inertial mass of the object—in fact, it is what we call the object’s weight—but since to get the acceleration you have to divide the force by the inertial mass, that cancels out, and a ends up being the same for all objects, regardless of how heavy they are.
Now that we have this result under our belt, we can move on to the slightly more challenging case of two objects of comparable masses interacting through a potential energy function that must be, a function of just the relative coordinate x12=x2−x1.
I claim that in that case you can again get the force on object 1, F21, by taking the derivative of U(x2−x1) with respect to x1 (leaving x2 alone), and reciprocally, you get F12 by taking the derivative of U(x2−x1) with respect to x2. Here is how it works, again using the chain rule:
F21=−ddx1U(x12)=−dUdx12ddx1(x2−x1)=dUdx12F12=−ddx2U(x12)=−dUdx12ddx2(x2−x1)=−dUdx12
and you can see that this automatically ensures that F21=−F12. In fact, it was in order to ensure this that I required that U should depend only on the difference of x1 and x2, rather than on each one separately. Since we got the condition F21=−F12 originally from conservation of momentum, you can see now how the two things are related1.
The only example we have seen so far of this kind of potential energy function was in Chapter 9, for two carts interacting through an “ideal” spring. I told you there that the potential energy of the system could be written as 12k(x2−x1−x0)2, where k was the “spring constant” and x0 the relaxed length of the spring. If you apply Eqs. (21.1.8) to this function, you will find that the force exerted (through the spring) by cart 2 on cart 1 is
F21=k(x2−x1−x0).
Note that this force will be negative under the assumptions we made last chapter, namely, that cart 2 is on the right, cart 1 on the left, and the spring is compressed, so that x2−x1<x0. Similarly,
F12=−k(x2−x1−x0)
and this one, as it should, is positive.
The results (???) and (???) basically tell you what we mean by an “ideal spring” in physics: it is a spring that pulls (if stretched) or pushes (if compressed) with a force that is proportional to the change from its equilibrium length. Thus, if you fasten one end of the spring at x = 0, and stretch it or compress it so that the other end is at x, the spring will respond by exerting a force
As you can see, this is negative if x>x0>0 (spring stretched, pulling force) and positive if x<x0 (spring compressed, pushing force). In fact, the spring exerts an equal (in magnitude) and opposite (in direction) force at the other end (the one attached to the wall), so Equation (???) only gives the correct sign of the force at the end that is denoted by the coordinate value x. Equations (???) and (???) are a bit clearer in this respect: Equation (???) gives the correct sign of the force at point x1, and Equation (???) the correct sign at point x2.
Figure 21.1.1 shows, in black, all the forces exerted by a spring with one fixed end, according as to whether it is relaxed, compressed, or stretched. I have assumed that it is pushed or pulled by a hand (not shown) at the “free” end, hence the subscript “h”, whereas the subscript “w” stands for “wall.” Note that the wall and the hand, in turn, exert equal and opposite forces on the spring, shown in red in the figure.
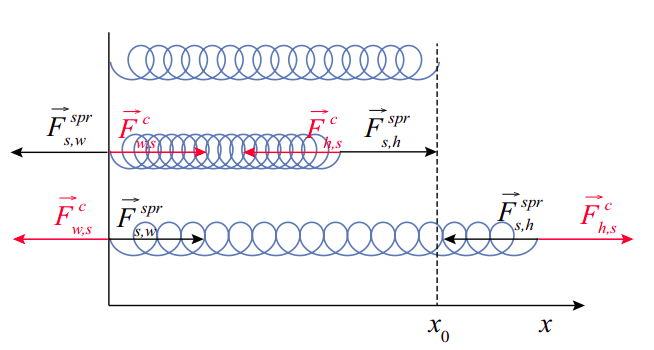
Equation (???) is generally referred to as Hooke’s law, after the British scientist Robert Hooke (a contemporary of Newton). Of course, it is not a “law” at all, merely a useful approximation to the way most springs behave as long as you do not stretch them or compress them too much2.
A note on the way the forces have been labeled in Figure 21.1.1. I have used the generic symbol “c”, which stands for “contact,” to indicate the type of force exerted by the wall and the hand on the spring. In fact, since each pair of forces (by the hand on the spring and by the spring on the hand, for instance), at the point of contact, arises from one and the same interaction, I should have used the same “type” notation for both, but it is widespread practice to use a superscript like “spr” to denote a force whose origin is, ultimately, a spring’s elasticity. This does not change the fact that the spring force, at the point where it is applied, is indeed a contact force.
So, next, a word on “contact” forces. Basically, what we mean by that is forces that arise where objects “touch,” and we mean this by opposition to what are called instead “field” forces (such as gravity, or magnetic or electrostatic forces) which “act at a distance.” The distinction is actually only meaningful at the macroscopic level, since at the microscopic level objects never really touch, and all forces are field forces, it is just that some are “long range” and some are “short range.” For our purposes, really, the word “contact” will just be a convenient, catch-all sort of moniker that we will use to label the force vectors when nothing more specific will do.
1The result (21.1.8) generalizes to more dimensions, but to do it properly you need vectors and partial derivative notation, and I’m already bending the notational rules a little bit here..
2Assuming that you can compress them! Some springs, such as slinkies, actually cannot be compressed because their coils are already in contact when they are relaxed. Nevertheless, Equation (???) will still apply approximately to such a spring when it is stretched, that is, when x>x0.


