1.2: Hooke’s Law
- Last updated
- Jan 15, 2019
- Save as PDF
- Page ID
- 17093

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Generate the mathematical expression of Hooke’s law
In mechanics (physics), Hooke’s law is an approximation of the response of elastic (i.e., springlike) bodies. It states: the extension of a spring is in direct proportion with the load applied to it. For instance, the spring is pulled downwards with either no load, Fp, or twice Fp.
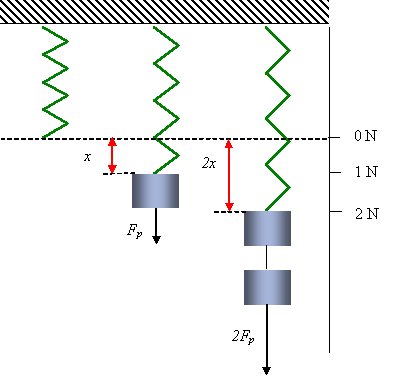
Diagram of Hooke’s Law: The extension of the spring is linearly proportional to the force.
Springs and Hooke’s Law: A brief overview of springs, Hooke’s Law, and elastic potential energy for algebra-based physics students.
Many materials obey this law of elasticity as long as the load does not exceed the material’s elastic limit. Materials for which Hooke’s law is a useful approximation are known as linear-elastic or “Hookean” materials. Hookean materials are broadly defined and include springs as well as muscular layers of the heart. In simple terms, Hooke’s law says that stress is directly proportional to strain. Mathematically, Hooke’s law is stated as:
F=−kx
where:
- x is the displacement of the spring’s end from its equilibrium position (a distance, in SI units: meters);
- F is the restoring force exerted by the spring on that end (in SI units: N or kg·m/s2); and
- k is a constant called the rate or spring constant (in SI units: N/m or kg/s2). When this holds, the behavior is said to be linear. If shown on a graph, the line should show a direct variation.
It’s possible for multiple springs to act on the same point. In such a case, Hooke’s law can still be applied. As with any other set of forces, the forces of many springs can be combined into one resultant force.
When Hooke’s law holds, the behavior is linear; if shown on a graph, the line depicting force as a function of displacement should show a direct variation. There is a negative sign on the right hand side of the equation because the restoring force always acts in the opposite direction of the displacement (for example, when a spring is stretched to the left, it pulls back to the right).
Hooke’s law is named after the 17th century British physicist Robert Hooke, and was first stated in 1660 as a Latin anagram, whose solution Hooke published in 1678 as Ut tensio, sic vis, meaning, “As the extension, so the force.”
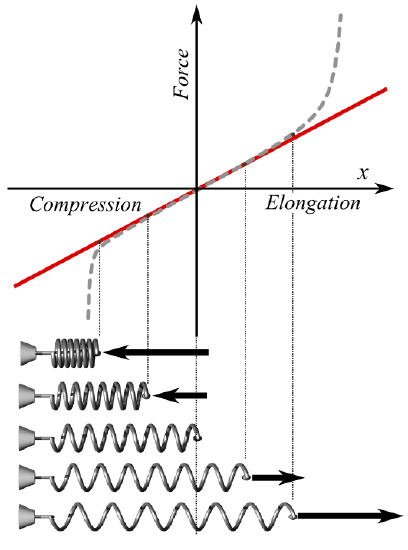
Hooke’s Law: The red line in this graph illustrates how force, F, varies with position according to Hooke’s law. The slope of this line corresponds to the spring constant k. The dotted line shows what the actual (experimental) plot of force might look like. The pictures of spring states at the bottom of the graph correspond to some points of the plot; the middle one is in the relaxed state (no force applied).
Elastic Potential Energy
If a force results in only deformation, with no thermal, sound, or kinetic energy, the work done is stored as elastic potential energy.
learning objectives
- Express elastic energy stored in a spring in a mathematical form
Elastic Potential Energy
In order to produce a deformation, work must be done. That is, a force must be exerted through a distance, whether you pluck a guitar string or compress a car spring. If the only result is deformation and no work goes into thermal, sound, or kinetic energy, then all the work is initially stored in the deformed object as some form of potential energy. Elastic energy is the potential mechanical energy stored in the configuration of a material or physical system when work is performed to distort its volume or shape. For example, the potential energy PEel stored in a spring is
PEel=12kx2
where k is the elastic constant and x is the displacement.
It is possible to calculate the work done in deforming a system in order to find the energy stored. This work is performed by an applied force Fapp. The applied force is exactly opposite to the restoring force (action-reaction), and so Fapp=kx. A graph shows the applied force versus deformation x for a system that can be described by Hooke’s law. Work done on the system is force multiplied by distance, which equals the area under the curve, or 12kx2 (Method A in the figure). Another way to determine the work is to note that the force increases linearly from 0 to kx, so that the average force is 12kx, the distance moved is x, and thus
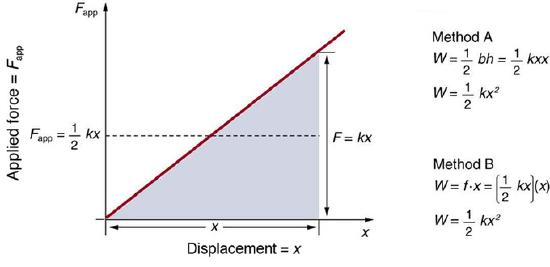
Applied force versus deformation: A graph of applied force versus distance for the deformation of a system that can be described by Hooke’s law is displayed. The work done on the system equals the area under the graph or the area of the triangle, which is half its base multiplied by its height, or W=12kx2.
W=Fappd=(12kx)(x)=12kx2 (Method B in the figure).
Elastic energy of or within a substance is static energy of configuration. It corresponds to energy stored principally by changing the inter-atomic distances between nuclei. Thermal energy is the randomized distribution of kinetic energy within the material, resulting in statistical fluctuations of the material about the equilibrium configuration. There is some interaction, however. For example, for some solid objects, twisting, bending, and other distortions may generate thermal energy, causing the material’s temperature to rise. This energy can also produce macroscopic vibrations sufficiently lacking in randomization to lead to oscillations that are merely the exchange between (elastic) potential energy within the object and the kinetic energy of motion of the object as a whole.
Key Points
- Mathematically, Hooke’s Law can be written as F=−kx.
- Many materials obey this law as long as the load does not exceed the material’s elastic limit.
- The rate or spring constant, k, relates the force to the extension in SI units: N/m or kg/s2.
- In order to produce a deformation, work must be done.
- The potential energy stored in a spring is given by PEel=12kx2, where k is the spring constant and x is the displacement.
- Deformation can also be converted into thermal energy or cause an object to begin oscillating.
Key Terms
- elasticity: The property by virtue of which a material deformed under the load can regain its original dimensions when unloaded
- deformation: A transformation; change of shape.
- kinetic energy: The energy possessed by an object because of its motion, equal to one half the mass of the body times the square of its velocity.
- oscillating: Moving in a repeated back-and-forth motion.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Hooke's law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Hooke's_law. License: CC BY-SA: Attribution-ShareAlike
- Free High School Science Texts Project, Mechanical Properties of Matter: Deformation of Materials. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m39533/latest/. License: CC BY: Attribution
- elasticity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/elasticity. License: CC BY-SA: Attribution-ShareAlike
- HookesLawForSpring-English.png. Provided by: Wikipedia. Located at: https://upload.wikimedia.org/Wikipedia/commons/f/f0/HookesLawForSpring-English.png. License: CC BY-SA: Attribution-ShareAlike
- Dinamometro. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:Dinamometro.jpg. License: CC BY-SA: Attribution-ShareAlike
- Springs and Hooke's Law. Located at: http://www.youtube.com/watch?v=6MhaPzGxfV8. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Elastic potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Elastic_potential_energy. License: CC BY-SA: Attribution-ShareAlike
- Elastic potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Elastic_potential_energy. License: CC BY-SA: Attribution-ShareAlike
- Elastic potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Elastic_potential_energy. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42240/latest/?collection=col11406/1.7. License: CC BY: Attribution
- deformation. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/deformation. License: CC BY-SA: Attribution-ShareAlike
- oscillating. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/oscillating. License: CC BY-SA: Attribution-ShareAlike
- kinetic energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/kinetic%20energy. License: CC BY-SA: Attribution-ShareAlike
- HookesLawForSpring-English.png. Provided by: Wikipedia. Located at: https://upload.wikimedia.org/Wikipedia/commons/f/f0/HookesLawForSpring-English.png. License: CC BY-SA: Attribution-ShareAlike
- Dinamometro. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:Dinamometro.jpg. License: CC BY-SA: Attribution-ShareAlike
- Springs and Hooke's Law. Located at: http://www.youtube.com/watch?v=6MhaPzGxfV8. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, College Physics. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42240/latest/?collection=col11406/1.7. License: CC BY: Attribution


