4.E: Dynamics- Force and Newton's Laws of Motion (Exercises)
- Last updated
- Jul 16, 2020
- Save as PDF
- Page ID
- 26511
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
4.1: Development of Force Concept
1. Propose a force standard different from the example of a stretched spring discussed in the text. Your standard must be capable of producing the same force repeatedly.
2. What properties do forces have that allow us to classify them as vectors?
4.2: Newton’s First Law of Motion: Inertia
3. How are inertia and mass related?
4. What is the relationship between weight and mass? Which is an intrinsic, unchanging property of a body?
4.3: Newton’s Second Law of Motion: Concept of a System
5. Which statement is correct? Explain your answer and give an example.
(a) Net force causes motion.
(b) Net force causes change in motion.
6. Why can we neglect forces such as those holding a body together when we apply Newton’s second law of motion?
7. Explain how the choice of the “system of interest” affects which forces must be considered when applying Newton’s second law of motion.
8. Describe a situation in which the net external force on a system is not zero, yet its speed remains constant.
9. system can have a nonzero velocity while the net external force on it is zero. Describe such a situation.
10. A rock is thrown straight up. What is the net external force acting on the rock when it is at the top of its trajectory?
11. (a) Give an example of different net external forces acting on the same system to produce different accelerations.
(b) Give an example of the same net external force acting on systems of different masses, producing different accelerations.
(c) What law accurately describes both effects? State it in words and as an equation.
12. If the acceleration of a system is zero, are no external forces acting on it? What about internal forces? Explain your answers.
13. If a constant, nonzero force is applied to an object, what can you say about the velocity and acceleration of the object?
14. The gravitational force on the basketball in Figure is ignored. When gravity is taken into account, what is the direction of the net external force on the basketball—above horizontal, below horizontal, or still horizontal?
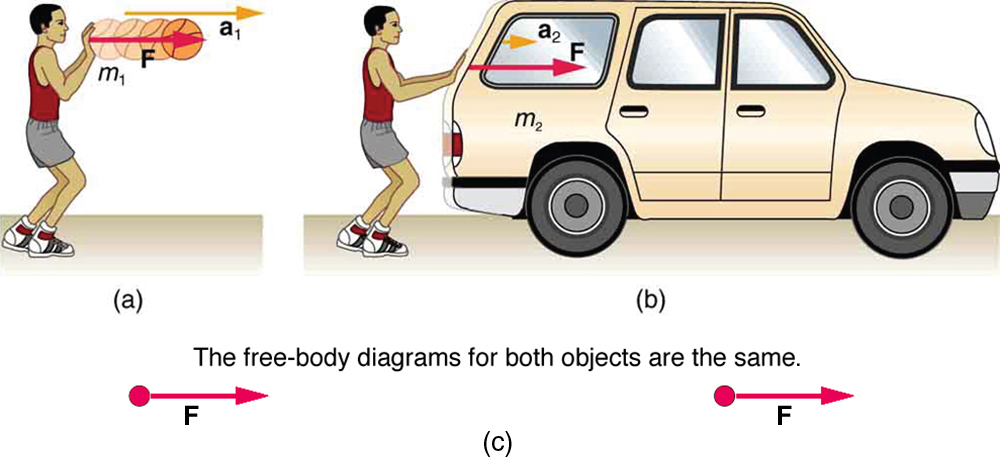
4.4: Newton’s Third Law of Motion: Symmetry in Forces
15. When you take off in a jet aircraft, there is a sensation of being pushed back into the seat. Explain why you move backward in the seat—is there really a force backward on you? (The same reasoning explains whiplash injuries, in which the head is apparently thrown backward.)
16. A device used since the 1940s to measure the kick or recoil of the body due to heart beats is the “ballistocardiograph.” What physics principle(s) are involved here to measure the force of cardiac contraction? How might we construct such a device?
17. Describe a situation in which one system exerts a force on another and, as a consequence, experiences a force that is equal in magnitude and opposite in direction. Which of Newton’s laws of motion apply?
18. Why does an ordinary rifle recoil (kick backward) when fired? The barrel of a recoilless rifle is open at both ends. Describe how Newton’s third law applies when one is fired. Can you safely stand close behind one when it is fired?
19. An American football lineman reasons that it is senseless to try to out-push the opposing player, since no matter how hard he pushes he will experience an equal and opposite force from the other player. Use Newton’s laws and draw a free-body diagram of an appropriate system to explain how he can still out-push the opposition if he is strong enough.
20. Newton’s third law of motion tells us that forces always occur in pairs of equal and opposite magnitude. Explain how the choice of the “system of interest” affects whether one such pair of forces cancels.
4.5: Normal, Tension, and Other Examples of Forces
21. If a leg is suspended by a traction setup as shown in Figure, what is the tension in the rope?
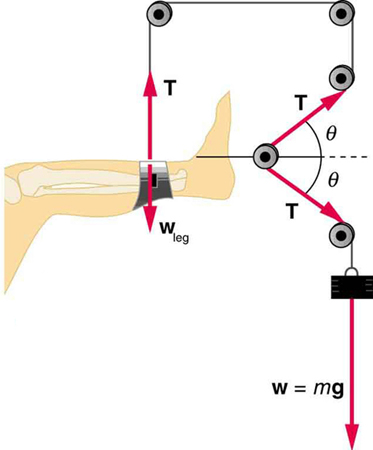
A leg is suspended by a traction system in which wires are used to transmit forces. Frictionless pulleys change the direction of the force T without changing its magnitude.
22. In a traction setup for a broken bone, with pulleys and rope available, how might we be able to increase the force along the tibia using the same weight? (See Figure.) (Note that the tibia is the shin bone shown in this image.)
4.7: Further Applications of Newton’s Laws of Motion
23. To simulate the apparent weightlessness of space orbit, astronauts are trained in the hold of a cargo aircraft that is accelerating downward at g. Why will they appear to be weightless, as measured by standing on a bathroom scale, in this accelerated frame of reference? Is there any difference between their apparent weightlessness in orbit and in the aircraft?
24. A cartoon shows the toupee coming off the head of an elevator passenger when the elevator rapidly stops during an upward ride. Can this really happen without the person being tied to the floor of the elevator? Explain your answer.
4.8: Extended Topic: The Four Basic Forces—An Introduction
25. Explain, in terms of the properties of the four basic forces, why people notice the gravitational force acting on their bodies if it is such a comparatively weak force.
26. What is the dominant force between astronomical objects? Why are the other three basic forces less significant over these very large distances?
27. Give a detailed example of how the exchange of a particle can result in an attractive force. (For example, consider one child pulling a toy out of the hands of another.)
Problems & Exercises
4.3: Newton’s Second Law of Motion: Concept of a System
You may assume data taken from illustrations is accurate to three digits.
28. A 63.0-kg sprinter starts a race with an acceleration of 4.20m/s2. What is the net external force on him?
Solution
265 N
29. If the sprinter from the previous problem accelerates at that rate for 20 m, and then maintains that velocity for the remainder of the 100-m dash, what will be his time for the race?
30. A cleaner pushes a 4.50-kg laundry cart in such a way that the net external force on it is 60.0 N. Calculate the magnitude of its acceleration.
Solution
13.3m/s2
31. Since astronauts in orbit are apparently weightless, a clever method of measuring their masses is needed to monitor their mass gains or losses to adjust diets. One way to do this is to exert a known force on an astronaut and measure the acceleration produced. Suppose a net external force of 50.0 N is exerted and the astronaut’s acceleration is measured to be 0.893m/s2.
(a) Calculate her mass.
(b) By exerting a force on the astronaut, the vehicle in which they orbit experiences an equal and opposite force. Discuss how this would affect the measurement of the astronaut’s acceleration. Propose a method in which recoil of the vehicle is avoided.
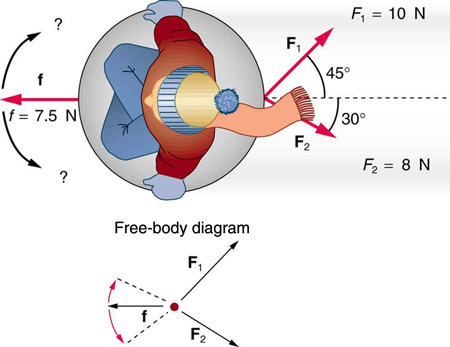
32. In Figure 4.4.3, the net external force on the 24-kg mower is stated to be 51 N. If the force of friction opposing the motion is 24 N, what force F (in newtons) is the person exerting on the mower? Suppose the mower is moving at 1.5 m/s when the force F is removed. How far will the mower go before stopping?
Solution
1.1 m
33. The same rocket sled drawn in Figure is decelerated at a rate of 196m/s2. What force is necessary to produce this deceleration? Assume that the rockets are off. The mass of the system is 2100 kg.
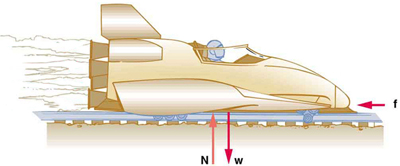
34. (a) If the rocket sled shown in Figure starts with only one rocket burning, what is the magnitude of its acceleration? Assume that the mass of the system is 2100 kg, the thrust T is 2.4×104 N, and the force of friction opposing the motion is known to be 650 N.
(b) Why is the acceleration not one-fourth of what it is with all rockets burning?
Solution
(a) 11m/s2
(b) The acceleration is not one-fourth of what it was with all rockets burning because the frictional force is still as large as it was with all rockets burning.
35. What is the deceleration of the rocket sled if it comes to rest in 1.1 s from a speed of 1000 km/h? (Such deceleration caused one test subject to black out and have temporary blindness.)
36. Suppose two children push horizontally, but in exactly opposite directions, on a third child in a wagon. The first child exerts a force of 75.0 N, the second a force of 90.0 N, friction is 12.0 N, and the mass of the third child plus wagon is 23.0 kg.
(a) What is the system of interest if the acceleration of the child in the wagon is to be calculated?
(b) Draw a free-body diagram, including all forces acting on the system.
(c) Calculate the acceleration.
(d) What would the acceleration be if friction were 15.0 N?
Solution
(a) The system is the child in the wagon plus the wagon.
(b)
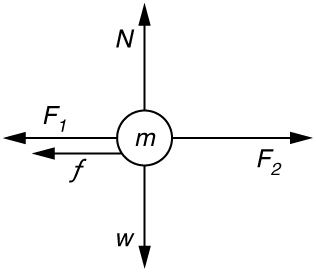
(c) a=0.130m/s2 in the direction of the second child’s push.
(d) a=0.00m/s2
37. A powerful motorcycle can produce an acceleration of 3.50m/s2while traveling at 90.0 km/h. At that speed the forces resisting motion, including friction and air resistance, total 400 N. (Air resistance is analogous to air friction. It always opposes the motion of an object.) What is the magnitude of the force the motorcycle exerts backward on the ground to produce its acceleration if the mass of the motorcycle with rider is 245 kg?
38. The rocket sled shown in Figure accelerates at a rate of 49.0m/s2. Its passenger has a mass of 75.0 kg.
(a) Calculate the horizontal component of the force the seat exerts against his body. Compare this with his weight by using a ratio.
(b) Calculate the direction and magnitude of the total force the seat exerts against his body.
Solution
(a) 3.68×103N. This force is 5.00 times greater than his weight.
(b) \displaystyle 3750 N; 11.3ºabove horizontal

39. Repeat the previous problem for the situation in which the rocket sled decelerates at a rate of \displaystyle 201 m/s^2. In this problem, the forces are exerted by the seat and restraining belts.
40. The weight of an astronaut plus his space suit on the Moon is only 250 N. How much do they weigh on Earth? What is the mass on the Moon? On Earth?
Solution
\displaystyle 1.5×10^3N,150 kg,150 kg
41. Suppose the mass of a fully loaded module in which astronauts take off from the Moon is 10,000 kg. The thrust of its engines is 30,000 N. (a) Calculate its the magnitude of acceleration in a vertical takeoff from the Moon. (b) Could it lift off from Earth? If not, why not? If it could, calculate the magnitude of its acceleration.
4.4: Newton’s Third Law of Motion: Symmetry in Forces
42. What net external force is exerted on a 1100-kg artillery shell fired from a battleship if the shell is accelerated at \displaystyle 2.40×10^4m/s^2? What is the magnitude of the force exerted on the ship by the artillery shell?
Solution
Force on shell: \displaystyle 2.64×10^7N
Force exerted on ship = \displaystyle −2.64×10^7N, by Newton’s third law
43. A brave but inadequate rugby player is being pushed backward by an opposing player who is exerting a force of 800 N on him. The mass of the losing player plus equipment is 90.0 kg, and he is accelerating at 1.20m/s2 size 12{1 "." "20"" m/s" rSup { size 8{2} } } {} backward. (a) What is the force of friction between the losing player’s feet and the grass? (b) What force does the winning player exert on the ground to move forward if his mass plus equipment is 110 kg? (c) Draw a sketch of the situation showing the system of interest used to solve each part. For this situation, draw a free-body diagram and write the net force equation.
4.5: Normal, Tension, and Other Examples of Forces
44. Two teams of nine members each engage in a tug of war. Each of the first team’s members has an average mass of 68 kg and exerts an average force of 1350 N horizontally. Each of the second team’s members has an average mass of 73 kg and exerts an average force of 1365 N horizontally.
(a) What is magnitude of the acceleration of the two teams?
(b) What is the tension in the section of rope between the teams?
Solution
a. \displaystyle 0.11 m/s^2
b. \displaystyle 1.2×10^4N
45. What force does a trampoline have to apply to a 45.0-kg gymnast to accelerate her straight up at \displaystyle 7.50 m/s^2? Note that the answer is independent of the velocity of the gymnast—she can be moving either up or down, or be stationary.
46. (a) Calculate the tension in a vertical strand of spider web if a spider of mass \displaystyle 8.00×10^{−5}kg hangs motionless on it.
(b) Calculate the tension in a horizontal strand of spider web if the same spider sits motionless in the middle of it much like the tightrope walker in Figure. The strand sags at an angle of \displaystyle 12º below the horizontal. Compare this with the tension in the vertical strand (find their ratio).
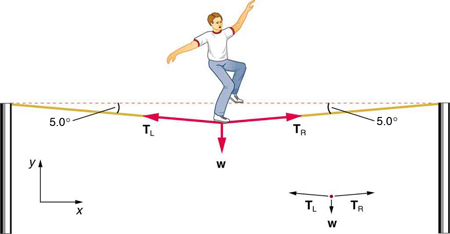
Solution
(a) \displaystyle 7.84×10^{-4}N
(b) \displaystyle 1.89×10^{–3}N. This is 2.41 times the tension in the vertical strand.
47. Suppose a 60.0-kg gymnast climbs a rope.
(a) What is the tension in the rope if he climbs at a constant speed?
(b) What is the tension in the rope if he accelerates upward at a rate of \displaystyle 1.50 m/s^2?
48. Show that, as stated in the text, a force \displaystyle F_{⊥} exerted on a flexible medium at its center and perpendicular to its length (such as on the tightrope wire in Figure) gives rise to a tension of magnitude \displaystyle T=\frac{F_⊥}{2sin(θ)}.
Solution
Newton’s second law applied in vertical direction gives
\displaystyle F_y=F−2Tsinθ=0
\displaystyle F=2Tsinθ
\displaystyle T=\frac{F}{2 sinθ}.
49. Consider the baby being weighed in Figure.
(a) What is the mass of the child and basket if a scale reading of 55 N is observed?
(b) What is the tension \displaystyle T_1 in the cord attaching the baby to the scale?
(c) What is the tension \displaystyle T_2 in the cord attaching the scale to the ceiling, if the scale has a mass of 0.500 kg?
(d) Draw a sketch of the situation indicating the system of interest used to solve each part. The masses of the cords are negligible.
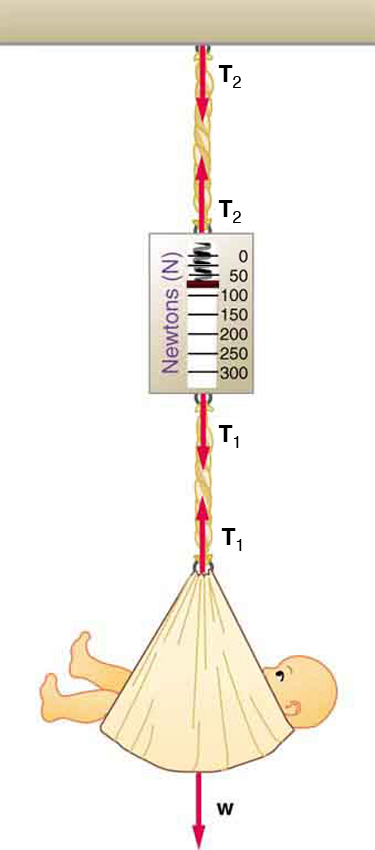
A baby is weighed using a spring scale.
4.6: Problem-Solving Strategies
50. A \displaystyle 5.00×10^5-kg rocket is accelerating straight up. Its engines produce \displaystyle 1.250×10^7N of thrust, and air resistance is \displaystyle 4.50×10^6N. What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
Solution
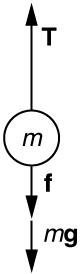
Using the free-body diagram:
\displaystyle F_{net}=T−f−mg=ma
so that
\displaystyle a=\frac{T−f−mg}{m}=\frac{1.250×10^7N−4.50×10^6N−(5.00×10^5kg)(9.80 m/s^2)}{5.00×10^5kg}=6.20m/s^2
51. The wheels of a midsize car exert a force of 2100 N backward on the road to accelerate the car in the forward direction. If the force of friction including air resistance is 250 N and the acceleration of the car is \displaystyle 1.80 m/s^2, what is the mass of the car plus its occupants? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. For this situation, draw a free-body diagram and write the net force equation.
52. Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
Solution
1.Use Newton’s laws of motion.
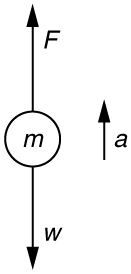
2. Given : \displaystyle a=4.00g=(4.00)(9.80 m/s^2)=39.2m/s^2; m=70.0 kg.
Find: \displaystyle F
3. \displaystyle \sum{F=+F−w=ma,} so that \displaystyle F=ma+w=ma+mg=m(a+g)
\displaystyle F=(70.0 kg)[(39.2 m/s^2)+(9.80 m/s^2)]=3.43×10^3N The force exerted by the high-jumper is actually down on the ground, but F size 12{F} is up from the ground and makes him jump.
4. This result is reasonable, since it is quite possible for a person to exert a force of the magnitude of \displaystyle 10^3N
53. When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
54. A freight train consists of two \displaystyle 8.00×10^4-kg engines and 45 cars with average masses of \displaystyle 5.50×10^4kg.
(a) What force must each engine exert backward on the track to accelerate the train at a rate of \displaystyle 5.00×10^{–2}m/s^2 if the force of friction is \displaystyle 7.50×10^5N, assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems.
(b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
Solution
(a) \displaystyle 4.41×10^5N
(b) \displaystyle 1.50×10^5N
55. Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor.
(a) An 1800-kg tractor exerts a force of \displaystyle 1.75×10^4N backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is \displaystyle 0.150 m/s^2, what is the mass of the airplane?
(b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane.
(c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.
56. A 1100-kg car pulls a boat on a trailer.
(a) What total force resists the motion of the car, boat, and trailer, if the car exerts a 1900-N force on the road and produces an acceleration of \displaystyle 0.550 m/s^2? The mass of the boat plus trailer is 700 kg.
(b) What is the force in the hitch between the car and the trailer if 80% of the resisting forces are experienced by the boat and trailer?
Solution
(a) \displaystyle 910 N
(b) \displaystyle 1.11×10^3N
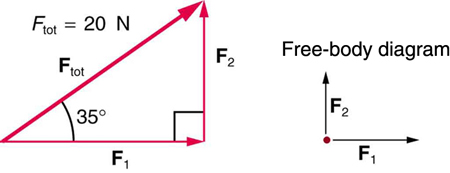
57. (a) Find the magnitudes of the forces \displaystyle F_1 and \displaystyle F_2 that add to give the total force \displaystyle F_{tot} shown in Figure. This may be done either graphically or by using trigonometry.
(b) Show graphically that the same total force is obtained independent of the order of addition of \displaystyle F_1 and \displaystyle F_2
(c) Find the direction and magnitude of some other pair of vectors that add to give \displaystyle F_{tot}. Draw these to scale on the same drawing used in part (b) or a similar picture.
58. Two children pull a third child on a snow saucer sled exerting forces \displaystyle F_1 and \displaystyle F_2 as shown from above in Figure. Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of \displaystyle F_1 and \displaystyle F_2.
Solution
\displaystyle a=0.139 m/s, θ=12.4º north of east
An overhead view of a child sitting on a snow saucer sled.
59. Suppose your car was mired deeply in the mud and you wanted to use the method illustrated in Figure to pull it out.
(a) What force would you have to exert perpendicular to the center of the rope to produce a force of 12,000 N on the car if the angle is 2.00°? In this part, explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
(b) Real ropes stretch under such forces. What force would be exerted on the car if the angle increases to 7.00° and you still apply the force found in part (a) to its center?

60. What force is exerted on the tooth in Figure if the tension in the wire is 25.0 N? Note that the force applied to the tooth is smaller than the tension in the wire, but this is necessitated by practical considerations of how force can be applied in the mouth. Explicitly show how you follow steps in the Problem-Solving Strategy for Newton’s laws of motion.
Solution
1. Use Newton’s laws since we are looking for forces.
2. Draw a free-body diagram:
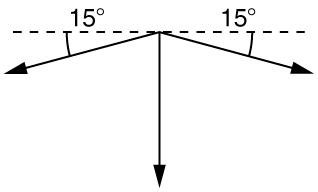
3. The tension is given as \displaystyle T=25.0 N. Find \displaystyle F_{app}. Using Newton’s laws gives: \displaystyle Σ F_y=0, so that applied force is due to the y-components of the two tensions: \displaystyle F_{app}=2Tsinθ=2(25.0 N)sin(15º)=12.9 N
The x-components of the tension cancel. \displaystyle ∑F_x=0.
4. This seems reasonable, since the applied tensions should be greater than the force applied to the tooth.
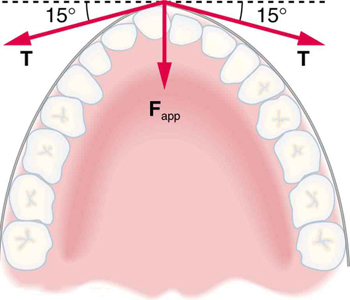
Braces are used to apply forces to teeth to realign them. Shown in this figure are the tensions applied by the wire to the protruding tooth. The total force applied to the tooth by the wire, \displaystyle F_{app}, points straight toward the back of the mouth.
61. Figure shows Superhero and Trusty Sidekick hanging motionless from a rope. Superhero’s mass is 90.0 kg, while Trusty Sidekick’s is 55.0 kg, and the mass of the rope is negligible.
(a) Draw a free-body diagram of the situation showing all forces acting on Superhero, Trusty Sidekick, and the rope.
(b) Find the tension in the rope above Superhero.
(c) Find the tension in the rope between Superhero and Trusty Sidekick. Indicate on your free-body diagram the system of interest used to solve each part.

Superhero and Trusty Sidekick hang motionless on a rope as they try to figure out what to do next. Will the tension be the same everywhere in the rope?
62. A nurse pushes a cart by exerting a force on the handle at a downward angle \displaystyle 35.0º below the horizontal. The loaded cart has a mass of 28.0 kg, and the force of friction is 60.0 N.
(a) Draw a free-body diagram for the system of interest.
(b) What force must the nurse exert to move at a constant velocity?
63. Construct Your Own Problem
Consider the tension in an elevator cable during the time the elevator starts from rest and accelerates its load upward to some cruising velocity. Taking the elevator and its load to be the system of interest, draw a free-body diagram. Then calculate the tension in the cable. Among the things to consider are the mass of the elevator and its load, the final velocity, and the time taken to reach that velocity.
64. Construct Your Own Problem
Consider two people pushing a toboggan with four children on it up a snow-covered slope. Construct a problem in which you calculate the acceleration of the toboggan and its load. Include a free-body diagram of the appropriate system of interest as the basis for your analysis. Show vector forces and their components and explain the choice of coordinates. Among the things to be considered are the forces exerted by those pushing, the angle of the slope, and the masses of the toboggan and children.
65. Unreasonable Results
(a) Repeat Exercise, but assume an acceleration of \displaystyle 1.20 m/s^2 is produced.
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, and why is it unreasonable?
66. Unreasonable Results
(a) What is the initial acceleration of a rocket that has a mass of \displaystyle 1.50×10^6kg at takeoff, the engines of which produce a thrust of \displaystyle 2.00×10^6N? Do not neglect gravity.
(b) What is unreasonable about the result? (This result has been unintentionally achieved by several real rockets.)
(c) Which premise is unreasonable, or which premises are inconsistent? (You may find it useful to compare this problem to the rocket problem earlier in this section.)
4.7: Further Applications of Newton’s Laws of Motion
67. A flea jumps by exerting a force of \displaystyle 1.20×10^{−5}N straight down on the ground. A breeze blowing on the flea parallel to the ground exerts a force of \displaystyle 0.500×10^{−6}N on the flea. Find the direction and magnitude of the acceleration of the flea if its mass is \displaystyle 6.00×10^{−7}kg. Do not neglect the gravitational force.
Solution
\displaystyle 10.2m/s^2, 4.67º from vertical
68. Two muscles in the back of the leg pull upward on the Achilles tendon, as shown in Figure. (These muscles are called the medial and lateral heads of the gastrocnemius muscle.) Find the magnitude and direction of the total force on the Achilles tendon. What type of movement could be caused by this force?
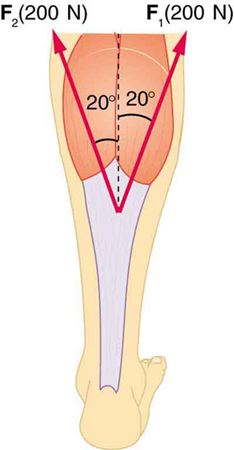
Achilles tendon
69. A 76.0-kg person is being pulled away from a burning building as shown in Figure. Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.
Solution
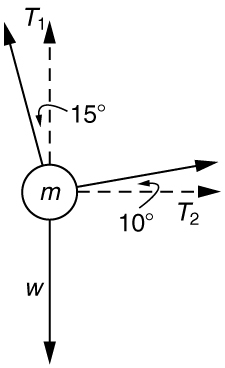
\displaystyle T_1=736 N
\displaystyle T_2=194 N
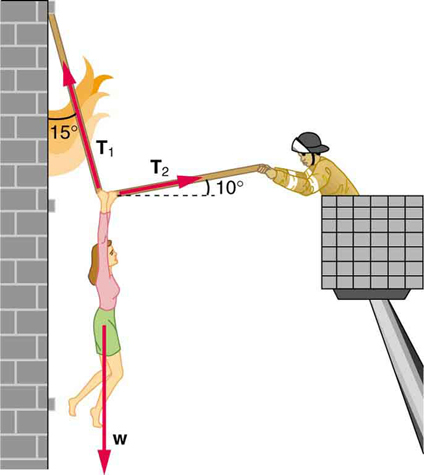
The force \displaystyle T_2 needed to hold steady the person being rescued from the fire is less than her weight and less than the force \displaystyle T_1 size 12{T rSub { size 8{1} } } {} in the other rope, since the more vertical rope supports a greater part of her weight (a vertical force).
70. Integrated Concepts
A 35.0-kg dolphin decelerates from 12.0 to 7.50 m/s in 2.30 s to join another dolphin in play. What average force was exerted to slow him if he was moving horizontally? (The gravitational force is balanced by the buoyant force of the water.)
71. Integrated Concepts
When starting a foot race, a 70.0-kg sprinter exerts an average force of 650 N backward on the ground for 0.800 s.
(a) What is his final speed?
(b) How far does he travel?
Solution
(a) \displaystyle 7.43 m/s
(b) \displaystyle 2.97 m
72. Integrated Concepts
A large rocket has a mass of \displaystyle 2.00×10^6kg at takeoff, and its engines produce a thrust of \displaystyle 3.50×10^7N.
(a) Find its initial acceleration if it takes off vertically.
(b) How long does it take to reach a velocity of 120 km/h straight up, assuming constant mass and thrust?
(c) In reality, the mass of a rocket decreases significantly as its fuel is consumed. Describe qualitatively how this affects the acceleration and time for this motion.
73. Integrated Concepts
A basketball player jumps straight up for a ball. To do this, he lowers his body 0.300 m and then accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the floor.
(a) Calculate his velocity when he leaves the floor.
(b) Calculate his acceleration while he is straightening his legs. He goes from zero to the velocity found in part (a) in a distance of 0.300 m.
(c) Calculate the force he exerts on the floor to do this, given that his mass is 110 kg.
Solution
(a) \displaystyle 4.20 m/s
(b) \displaystyle 29.4m/s^2
(c) \displaystyle 4.31×10^3N
74. Integrated Concepts
A 2.50-kg fireworks shell is fired straight up from a mortar and reaches a height of 110 m.
(a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar.
(b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in (a).
(c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.
75. Integrated Concepts Repeat Exercise for a shell fired at an angle \displaystyle 10.0º from the vertical.
Solution
(a) \displaystyle 47.1 m/s
(b) \displaystyle 2.47×10^3m/s^2
(c) \displaystyle 6.18×10^3N .
76. Integrated Concepts
An elevator filled with passengers has a mass of 1700 kg.
(a) The elevator accelerates upward from rest at a rate of \displaystyle 1.20 m/s^2. Calculate the tension in the cable supporting the elevator.
(b) The elevator continues upward at constant velocity for 8.50 s. What is the tension in the cable during this time?
(c) The elevator decelerates at a rate of \displaystyle 0.600 m/s^2 for 3.00 s. What is the tension in the cable during deceleration?
(d) How high has the elevator moved above its original starting point, and what is its final velocity?
77. Unreasonable Results
(a) What is the final velocity of a car originally traveling at 50.0 km/h that decelerates at a rate of \displaystyle 0.400 m/s^2 for 50.0 s?
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent?
78. Unreasonable Results
A 75.0-kg man stands on a bathroom scale in an elevator that accelerates from rest to 30.0 m/s in 2.00 s.
(a) Calculate the scale reading in newtons and compare it with his weight. (The scale exerts an upward force on him equal to its reading.)
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent?
4.8: Extended Topic: The Four Basic Forces—An Introduction
79. (a) What is the strength of the weak nuclear force relative to the strong nuclear force?
(b) What is the strength of the weak nuclear force relative to the electromagnetic force? Since the weak nuclear force acts at only very short distances, such as inside nuclei, where the strong and electromagnetic forces also act, it might seem surprising that we have any knowledge of it at all. We have such knowledge because the weak nuclear force is responsible for beta decay, a type of nuclear decay not explained by other forces.
Solution
(a) \displaystyle 1×10^{−13}
(b) \displaystyle 1×10^{−11}
80. (a) What is the ratio of the strength of the gravitational force to that of the strong nuclear force?
(b) What is the ratio of the strength of the gravitational force to that of the weak nuclear force?
(c) What is the ratio of the strength of the gravitational force to that of the electromagnetic force? What do your answers imply about the influence of the gravitational force on atomic nuclei?
81. What is the ratio of the strength of the strong nuclear force to that of the electromagnetic force? Based on this ratio, you might expect that the strong force dominates the nucleus, which is true for small nuclei. Large nuclei, however, have sizes greater than the range of the strong nuclear force. At these sizes, the electromagnetic force begins to affect nuclear stability. These facts will be used to explain nuclear fusion and fission later in this text.
Solution
\displaystyle 10^2
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


