7.1: Mathematical Continuum Descriptions of Membranes
( \newcommand{\kernel}{\mathrm{null}\,}\)
Membranes play an important role in cellular functions. They act as barriers to the outside environment, but also must allow the exchange of nutrients and waste. They must also be physically flexible to allow for cellular growth and movement, such as during cell division and migrations [1]. Membranes are composed of phospholipid bilayers. The phospholipids are amphipathic, containing a hydrophilic head and a hydrophobic tail. The membrane is composed of two adjacent layers of lipids, with the tails facing each other, and the hydrophilic heads facing the outside aqueous environment (Figure 7.1.1A). These membranes have a high aspect ratio with a low thickness of about 5 nm [1]. This is since the membrane is only two lipid molecules thick. However, the hydrophobic interior of the bilayer is a strong barrier against the transport of hydrophilic molecules across the membrane. Diffusion across the membrane is very slow for hydrophilic molecules and ions (transport requires transporter proteins) (Figure 7.1.1B). In addition, lipids can flip between leaflets, but this is very slow, as it requires the hydrophilic head pass through the hydrophobic region (Figure 7.1.1B). Lateral diffusion can be quite quick for lipids (~ 1 µm/s2 and even transmembrane proteins (0.1 µm/s2) (Figure 7.1.1B). Due to the described properties of the cellular membranes, they are commonly modeled as a 2-dimensional planar, elastic sheet in a 3-dimensional space (Figure 7.1.2). Biological structures like vesicles and even entire cells can be described as a closed form made by these sheets. These descriptions are known as continuum descriptions of the membrane. This is in contrast to molecular- and particle-based descriptions of the membrane, which focus on smaller time scales and length scales of membranes.

To understand the shape and dynamics of membranes, we will need to describe the geometry of the membrane surface itself. In addition, we will describe how the energy changes for different membrane configurations. In particular, we will look at how the energy changes when a membrane is stretched, bent, sheared and changed in the thickness (Figure 7.1.2).

Area Changes
The area deformation can easily be parameterized by a single variable Δa or a function Δa(x,y) if the area deformation is dependent on position. We can treat the lipids in the membrane as a system of connected elastic springs, with increasing the area equivalent to stretching the springs (Figure 7.1.3).
As such, the energy of stretching a piece of membrane is:
Ea=12KaΔa2a0
where Ka is the area modulus, which is intrinsic to the membrane, and a0 is some reference area from which change in area is calculated (i.e. Δa=a−a0). This equation is equivalent to a Hookean spring. Of course, when looking at a whole system, this term has to be integrated over the total area:
Ea=Ka2∫(Δaa0)2da
If the area change is constant over the surface of the membrane, then the integral reduces to Equation (1).
The area modulus has values of about 55-70 kBT or 230-290 mN/m [1].

Thickness Changes
Membrane compression can simply be described by a function w(x,y) that outputs the thickness at point (x,y). Again, we can model the thickness change as a system of springs (Figure 7.1.4). If the half-width of the membrane (essentially the lipid length in the membrane at equilibrium) is defined as w0, and the thickness is 2w0 (Figure 7.1.4), then we get a similar equation for the energy penalty of changing the thickness:
E thickness =Kt2∫(w(x,y)−w0w0)2da
where Kt is the stiffness for thickness variation, which is intrinsic to the membrane. It has units of energy/area and is approximately 60 kBT/nm2 [1].

Shear Changes:
Pure phospholipid membranes are essentially two-dimensional fluids. Due to the fluid nature of phospholipid bilayer, the membrane cannot support a shear strain and does not have a shear modulus. Therefore, as seen in Figure 7.1.2, static shear change does not deform a fluid membrane and does not cost any energy. However, most biological systems are not pure fluid membranes. For example, red blood cells have an underlying cytoskeletal network, which can support shear. If the shear elasticity is an important effect that needs to be modeled, it must be accounted for to model the equilibrium shapes and the dynamics of such cells. An example of this is described later.
An Interlude on Membrane Geometry
To understand how the energy costs of bending are determined, it is important to describe the geometry of the membrane.
If we take a reference two-dimensional plane, we can define a function h(x,y) that characterizes the height of the membrane above the reference plane at point (x,y). In most situations, this can accurately represent the shape of the membrane. This representation is known as the Monge parameterization (Figure 7.1.5). From the Monge parameterization, we can now calculate the curvature of a membrane. This is important as the free energy cost of bending the membrane is dependent on the curvature.

In a single dimension, if we have a smooth function y=h(x), then at a point x we can define the curvature κ(x) to be the inverse of the radius of a circle that closely approximates the curve at point x (Figure 7.1.6A):
κ=1R
It might be expected that a straight line has a curvature of 0. Indeed, since the circle that approximates the straight line is that of an infinite radius, the curvature is κ=1∞=0 (Figure 7.1.7).

To generalize this to the two-dimensional case, we could cut through the two-dimensional surface with a plane, obtaining a curve, from which we can calculate the curvature. However, depending on the orientation of the plane used to cut the surface, the value of the curvature for that orientation is different. It can be shown that the curvatures in two directions describe a single point on a surface. Specifically, there is one particular choice of orthogonal planes that the curvatures take extreme values. These values c1,c2 are known as the principal curvatures (Figure 7.1.6B). In fact, one can calculate the curvature in any other direction using the formula:
cX=c1cos2αX+c2sin2αX
where cx is the curvature in the direction X, and αX is the angle between the direction X and the direction belonging to curvature c1. These statements are known as the Euler Curvature Formula.
As an example of principal curvatures, the principal curvatures of a cylinder would be 1/R around the circumference of the cylinder (as the radius of curvature is R, but 0 along the length of the cylinder.
Other curvature quantities calculated from the principal curvatures are also commonly defined:
K=c1+c2KG=c1c2H=K2=c1+c22
where K is the is the extrinsic curvature, G is the Gaussian curvature, and H is the mean curvature.
With the Monge parameterization, the curvatures can be expressed in terms of the height function. It can be shown that the extrinsic curvature is:
K=∇⋅(∇h(r)√1+(∇h(r))2)
For a small gradient, the extrinsic curvature can be approximated as K≈Δh(r).
Why is the Monge parameterization and expressing the curvature using the parameterization important? These are important as the bending energy is dependent on the curvature, and to determine the equilibrium shapes of a membrane system, the height function that minimizes the total free energy of the system will be determined to represent the final membrane shape.
It is important to note that Monge parameterization is not the only way of describing a surface. It is not the most general parameterization or the most convenient parameterization in many cases. It will not work if there are folds or overlaps of the surface.
This is only an introduction to membrane/surface geometry, which itself is only a small part of the field of differential geometry. For more information on differential geometry in relation to membranes, the reader is referred to [3]. For a more general and advanced introduction to differential geometry, the reader is referred to [4].
Bending Changes – Helfrich theory:
The bending energy of a membrane is described by the well-known Helfrich theory. The Helfrich bending energy is defined in terms of the extrinsic and Gaussian curvature:
Ebend=∫(12κb(c1+c2−c0)2+¯κbc1c2)dA=∫(12κb(K−c0)+¯κbG)dA
where κb is the bending rigidity and ¯κb is the Gaussian bending rigidity. This equation also contains the spontaneous curvature c0. It is nonzero if there is some curvature in the membrane at an equilibrium state, which occurs if there is an asymmetric bilayer (different lipid composition for each monolayer). Typical values of κb is 10-20 kBT [1].
It is important to note that that Gaussian bending term can be ignored in most cases due to the Gauss-Bonnet theorem. The Gauss-Bonnet theorem says that if the topology of the system remains unchanged, the integral over the Gaussian curvature will be a constant. The topology (genus) can be determined by the number of holes/handles the surface has. For example, a sphere has no holes and therefore has a genus of 0, but a donut has one hole and a genus of 1. Therefore, unless the genus of the system changes, the Gaussian term vanishes. This is the case for many biological membranes. However, for complicated morphologies of the endoplasmic reticulum and mitochondria, Gaussian curvature could have a significant contribution as membrane holes, tubes, and tori are created and destroyed.
We can simplify the above equation for Monge parameterization, with no spontaneous curvature. It can be shown for the Monge parameterization that the area element is dA=dxdy√1+(∇h)2. For the small gradient approximation, this is equivalent to dA=(1+12(∇h)2)dxdy (based on a simple Taylor expansion). We can also penalize area stretching with a term 12∑(∇h)2 where Σ is membrane tension. Therefore, a Helfrich energy equation for a Monge parameterization, under the small gradient approximation, and includes bending and tension is:
Ebend=12∫dxdy[κb(Δh)2+Σ(∇h)2]
Vesicles and Free Energy Cost
Vesicles are spherical lipid bilayer structures. Vesicles are used for many cellular processes for transporting large amounts of cargo within cells or even between cells. An example of the latter is the transport of neurotransmitters between neurons at the synaptic cleft.
We can calculate the free energy cost of the vesicles. The principal curvatures are the same: 1/R Therefore, the free energy cost is:
Evesicle=κb2∫(2R)2dA=κb2(2R)24πR2=8πκb
Interestingly, this means there is a fixed energy cost to create a vesicle regardless of the size of the vesicle. If κb≈10kBT then Evesicle≈250kBT, which means there must be an active mechanism for the formation of vesicles in cells. Indeed vesicle-coating proteins like clathrin decrease this energy barrier such that vesicle formation is favorable.
Applications
Membrane tethers
When a pulling force is applied to a single point on a vesicle, it will generate an extruded membrane tubule known as membrane tethers. Membrane tethers have many biological implications. For example, neutrophils can use membrane tethers to attach to the endothelial wall when rolling. Membrane tethers also have an important role in the endomembrane system. In addition, the energetics and dynamics of membrane tethers are similar to that of other biological processes, such as endocytosis, and actin projections during cell motility.
Experiments use optical tweezers or molecular motors to apply a force at a single point on the membrane. We will use a simplified model (Figure 7.1.8) of the process where we have a sphere of radius R attached to a cylinder of radius r and length L. At the end of the cylinder is a hemispherical cap.

We can write the free energy of the vesicle+tether system by calculating the contributions of bending, area stretching, and compression. The bending energy of the system is:
Ebending=8πκb+πκbLr+4πκb=12πκb+πκbLr
The first term corresponds to the spherical vesicle (as demonstrated previously). The second term corresponds to the cylinder, which is calculated by squaring the sum of the principal curvatures (0+1r)2 and multiplying by the area. The last term corresponds to the hemispherical cap.
Area stretching also contributes to the free energy of the system:
Earea=Ka2(a−a0)2a0
where a0 is the reference area and a=4πR2+2πrL is the area of the system. The first term corresponds to a sphere of radius R and the second term corresponds to a cylinder of raidus r. Note that the area of the hemispherical cap 4πr2 is ignored as it is assumed r≪R,L.
Note that this system has no thickness change of the membrane and therefore does not contribute to the free energy of the system.
In the case of a closed bilayer like a vesicle, the pressure difference across the membrane Δp also contributes to the energy of the system:
EpV=−Δp∫dV=−Δp(43πR3+r2πL)
Again, the contribution of the hemispherical cap is ignored. The minus sign is present because excess internal pressure increases the volume.
Finally, the force pulling the membrane must also contribute to the free energy of the system:
Eload=−fL
where f is the force applied. The minus sign is present because increased force leads to a high tether length.
Summing equations 11, 12, 13, and 14 together, we get:
Etot=12πκb+πκbLr+Ka2(a−a0)2a0−Δp(43πR3+r2πL)−fL
At equilibrium, the total energy is minimized. Therefore, the equilibrium shape can be determined by minimizing the free energy.
In this case, we can take the derivatives of Equation 15 with respect to each of the variables to minimize the energy.
Note that
∂Earea∂R=Kaa−a0a0∂a∂R=τ8πR
where τ is the membrane surface tension, which can be related to area stretching by the formula τ=Ka(a−a0)a0. Similarly, it can be shown that ∂Earea/∂r=τ2πL and ∂Earea/∂L=τ2πr. Therefore:
∂Etot∂R=0→8πτR−4πΔpR2=0→Δp=2τR∂Etot∂r=0→−πκbLr2+2πτL−2πΔprL=0∂Etot∂L=0→πκb1r+2πτr−πΔpr2−f=0
![]() The first minimization leads to an equation known as the Laplace-Young relation, which is a well-known equation that relates the pressure difference Δp across a fluid interface (here the membrane) and the surface tension τ. A more general form takes into account both radii of curvature:
The first minimization leads to an equation known as the Laplace-Young relation, which is a well-known equation that relates the pressure difference Δp across a fluid interface (here the membrane) and the surface tension τ. A more general form takes into account both radii of curvature:
Δp=τ(1R1+1R2)
We can plug in the Laplace-Young relation into the other minimized equations:
−πκbLr2+2πτL−4πτrLR=0πκb1r+2πτr−f−2πτr2R=0
Since r≪R (Figure 7.1.8) the last terms can be ignored:
2πτL=πκbLr2
r=√κb2τ
πκb1r+2πτr−f=0→πκb√2τκb+2πτ√κb2τ=f
f=2π√2Kbτ
We now get a relation between the radius of tether, bending energy, and membrane tension. In addition, we get a relation between the force applied, bending energy and tension. Similar relations can actually be used to determining the bending rigidity κb using a micropipette aspiration and optical tweezers used to make membrane tethers [5].
A general framework of determining equilibrium shapes (variational calculus):
The previous section looked at how relationships between meaningful physical quantities can be derived if the shape of the system is known. This was done by calculating the free energy cost for the membrane shape and minimizing it with respect to the variables of the system. However, a different approach can also be taken. What if the physical quantities of the system are known, but the equilibrium shapes need to be determined? This can be done by minimizing an energy functional of the system, which is the basis of variational calculus.
We can define a functional as a function that assigns a scalar value for a given function. In this case, we can think of the free energy of the system Etot as a functional that is dependent on the height function h(x,y). Variational calculus provides tools to find functions that minimize the functionals. This is exactly what we need to determine the equilibrium shapes! Variational calculus can be used to find the shape function h(x,y) that minimizes the energy Etot
In variational calculus, in a one-dimensional case, the minimization of the functional:
J[y]=∫L(x,y,y′)dx
is solved by the solution of the differential equation:
∂L∂f−ddx∂L∂f′=0
where y=f(x) minimizes the functional. This equation is known as the Euler-Lagrange equation. Indeed, the equation for Etot has this form.
As a side note, many equations in physics have this form and the Euler-Lagrange equation is used. In fact, the dynamics of a physical system can be represented as a functional known as the Lagrangian, and solving the Euler-Lagrange equations for this Lagrangian lead to the equations of motion. This approach to classical mechanics is known as Lagrangian mechanics.
Going back to membranes, if we use Equation (9), we can get the following Euler-Lagrange equation:
κΔΔh−ΣΔh=0
This partial differential equation can be solved for the height function that describes the shape of the membrane at equilibrium. This is called the shape equation.
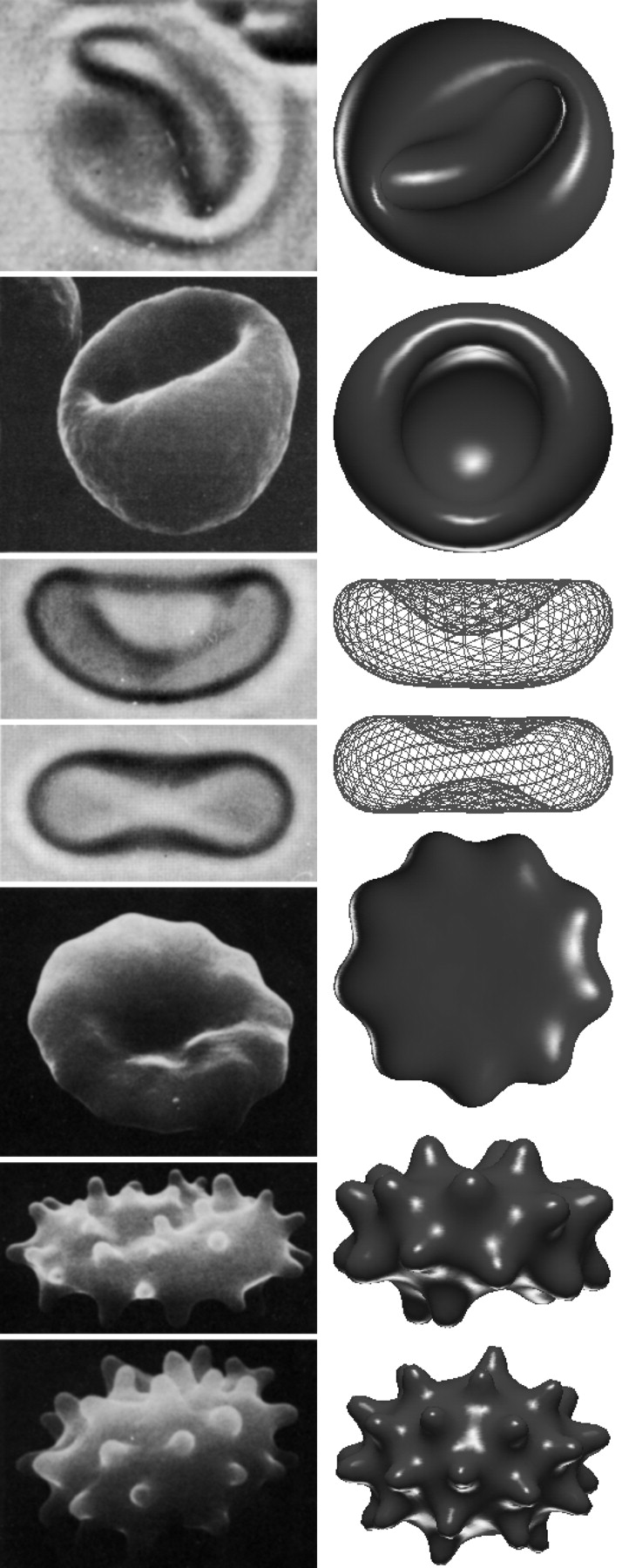
Minimization of red blood cells:
While solving the shape equations are non-trivial and won’t be shown here, some results in the case of red blood cells will instead be shown.
It is important to note that there are often two additional energy terms added to the Helfrich bending energy to obtain the total free energy for red blood cells.
When an initially flat membrane is bent, the outer monolayer is stretched, and the inner monolayer is compressed and the number of lipids per unit area is higher for the inner surface and lower for the outer surface. The energy cost of this is added to the model as the following model:
EADE=κADE2πAD2(ΔA−ΔA0)2
where κADE is a separate bending energy, which a material parameter, A is the membrane area, and D is the membrane thickness. This is known as the area-difference-elasticity (ADE) model.
In addition, an elastic term is added of the form:
Ee=KA2∮α2dA+μ∮βdA
where α2 and β2 are the local area and strain invariants, KA and μ are elastic moduli for stretching and strain, respectively.
When the total free energy Ebend+EADE+Ee is minimized, the equilibrium shapes of the red blood cells can be determined. The below Figure shows a comparison of the theoretically determined shapes and those that have been found experimentally.
References:
- Phillips, R.; Kondev, J.; Theriot, J.; Garcia, H. G. Physical Biology of the Cell, 2013, Garland Science, Taylor & Francis Group, LLC: Abingdon, UK.
- Boal, D. Mechanics of the Cell. Cambridge University Press: Cambridge, UK. 2002
- Deserno, Markus. Fluid Lipid Membranes – A Primer. Max-Planck-Institut fu ̈r Polymerforschung. Mainz, Germany. 2006
- Deserno, Markus. Notes on Differential Geometry. Max-Planck-Institut fu ̈r Polymerforschung. Mainz, Germany. 2004
- Bo, Lin, and Richard E. Waugh. “Determination of Bilayer Membrane Bending Stiffness by Tether Formation from Giant, Thin-Walled Vesicles.” Biophysical Journal, vol. 55, doi:10.1016/S0006-3495(89)82844-9. Accessed 13 June 2019.
- Li, Xuejin, et al. Continuum- and Particle-Based Modeling of Shapes and Dynamics of Red Blood Cells in Health and Disease. Soft Matter, vol. 9, no. 1, 2013, pp. 28–37., doi:10.1039/c2sm26891d.
- W., G. Lim H., et al. “Stomatocyte-Discocyte-Echinocyte Sequence of the Human Red Blood Cell: Evidence for the Bilayer- Couple Hypothesis from Membrane Mechanics.” Proceedings of the National Academy of Sciences, vol. 99, no. 26, 2002, pp. 16766–16769., doi:10.1073/pnas.202617299.



