2.10: S11. The Friedmann Equation - SOLUTIONS

Exercise 11.1.1

Answer

K.E. is $\frac{1}{2}mv^2$, where $v = \dot a \ell$, so the test particle's kinetic energy is

$$\begin{equation*} \begin{aligned} \frac{1}{2}m\dot a^2 \ell ^2 \end{aligned} \end{equation*}$$

Exercise 11.1.2

Answer

P.E. is $-\frac{GM(<d)m}{d}$, where by $M(<d)$ we mean the mass contained in the sphere of radius $d$, so $M(<d) = \frac{4}{3}\pi d^3 \rho.$

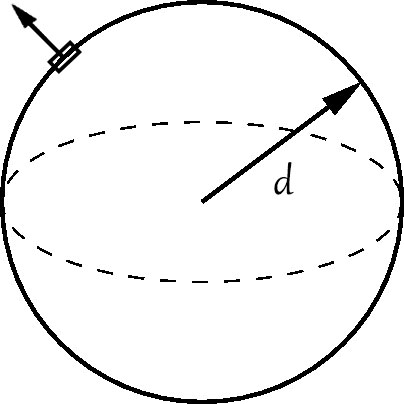
Therefore the test particle's potential energy is

$$\begin{equation*} \begin{aligned} -G \frac{4}{3} \pi \rho d^2 m \end{aligned} \end{equation*}$$

Exercise 11.1.3

Answer

$$\begin{equation*} \begin{aligned} \frac{1}{2}m\dot a^2 \ell ^2 - G \frac{4}{3} \pi \rho d^2 m = \kappa \end{aligned} \end{equation*}$$

Exercise 11.1.4

Answer

Recall that $d = a \ell \; \Longrightarrow \; \ell = \frac{d}{a}$, substituting this in and rearranging our equation we get

$$\begin{equation*} \begin{aligned} \frac{1}{2}md^2 \frac{\dot a^2}{a^2} - \frac{1}{2}md^2 \frac{8\pi G\rho}{3} = \kappa \end{aligned} \end{equation*}$$

dividing through by $\frac{1}{2}md^2$ gives

$$\begin{equation*} \begin{aligned} \frac{\dot a^2}{a^2} - \frac{8\pi G\rho}{3} = \frac{2\kappa}{m}\frac{1}{d^2} \end{aligned} \end{equation*}$$

Then we substitute back in $d = a \ell$ and solve for $\big(\frac{\dot a}{a}\big)^2$:

$$\begin{equation*} \begin{aligned} \left(\frac{\dot a}{a}\right)^2 = \frac{8\pi G \rho}{3} + \frac{2\kappa}{ml^2} \times \frac{1}{a^2} \end{aligned} \end{equation*}$$