1.25: Introduction to the Cosmic Microwave Background
( \newcommand{\kernel}{\mathrm{null}\,}\)
Discovery
As we have seen in our study of big bang nucleosynthesis, Alpher and Herman predicted the cosmic microwave background (CMB) in the 1940s. But it was decades until anyone mounted a serious campaign to look for this relic of the big bang. The delay seems astounding from our perspective, and yet nonetheless this is what happened. The prediction, of a relic of the big bang, that would not have been too difficult to detect, somehow did not garner much attention. The first effort to make measurements to detect the CMB was launched by a group at Princeton University in the early sixties. They had an extremely well-motivated set of observations in mind. They had the technical ability to build the instruments and make the measurements. They had the funding they needed. They just got started a little too late: in 1964 they were scooped by a pair of radio astronomers, a mere 30 miles to their east at Bell Labs, who had stumbled upon the cosmic relic accidentally. Life is not always fair.
Arno Penzias and Robert Wilson were the Bell Labs-employed radio astronomers, who, though they did not know it, were performing measurements of great historic importance. They had re-purposed a radio telescope, built for early experiments with satellite communication, to do some astronomy, such as measuring radio emission from a supernova remnant. As part of a process of characterizing their instrument and its noise properties, they made measurements away from any such sources. They were unable to reconcile the output from their radiometer, when the telescope was aimed at blank sky, with their estimates of the amount of noise there should be in their measurements. No matter where they pointed their telescope, the radiometer output exceeded what they expected from noise, consistent with a uniform background of microwaves.
The two groups became aware of each other's efforts (via some intermediaries), which led to them all realizing that the CMB had been detected. They agreed to write a pair of papers. The first was authored by Penzias and Wilson and titled "A Measurement of Excess Antenna Temperature at 4080 Mc/s." The second was written by the Princeton group and provided the cosmological interpretation of their measurement, simply titled "Cosmic Black-body Radiation." Penzias and Wilson received the 1978 Nobel Prize in Physics for their discovery.
The Last-Scattering Surface
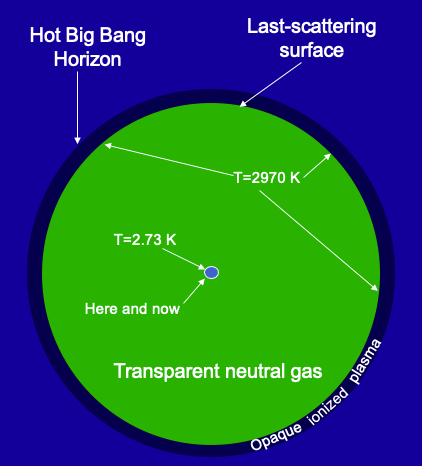 Before going much further it's worth having a picture in your mind of what we're looking at when we're looking at the CMB. Toward that end, consider the figure on the right, a cartoon of our past light cone. To see it as a cone, you'll have to use your imagination to lift the "Here and now" part up off the screen to be the tip of the cone, and then have the circle labeled as "Hot Big Bang Horizon" remain back down on the surface of the screen forming the base of the cone. The axis coming out of the screen is the temporal dimension. The center is our location in spacetime (where we are in space and when we are). Moving radially away from the center, one is moving away from us in comoving distance and, because we are staying on the cone, also moving back in time.
Before going much further it's worth having a picture in your mind of what we're looking at when we're looking at the CMB. Toward that end, consider the figure on the right, a cartoon of our past light cone. To see it as a cone, you'll have to use your imagination to lift the "Here and now" part up off the screen to be the tip of the cone, and then have the circle labeled as "Hot Big Bang Horizon" remain back down on the surface of the screen forming the base of the cone. The axis coming out of the screen is the temporal dimension. The center is our location in spacetime (where we are in space and when we are). Moving radially away from the center, one is moving away from us in comoving distance and, because we are staying on the cone, also moving back in time.
As we have already seen, if we assume a radiation-dominated universe we find that it reaches infinite density a finite time in the past. Further, even allowing for the transition from radiation domination to matter domination, and then to cosmological constant domination, a signal traveling at the speed of light from that time of infinite density until today will only travel a finite distance. We call that distance the past horizon. That distance is the radius of the circle labeled "Hot Big Bang Horizon."
But light can't travel stright to us from some time way back in the radiation-dominated era because the universe is filled with an opaque plasma. A plasma is the state of matter when it is sufficiently hot that the electrons are stripped away from the nuclei. Since light readily scatters off of free electrons, plasmas at sufficient density and sufficiently thick are opaque; light can't travel freely through them. However, as the universe expands, it cools, and the universe undergoes a transition from an opaque ionized plasma to a transparent neutral gas. We've labeled this transition on our diagram as the "Last-scattering surface" because this is where light that arrives here and now last scatters off of a free electron. We also refer to this epoch as "decoupling" because it is when light decouples from matter.
So, when we are detecting CMB photons, we are detecting light that, for the most part, last interacted with matter at the time of this transition. If our eyes were sensitive to light at microwave frequencies, when we looked up at the sky we would be seeing an image of this last-scattering surface. Now in the diagram the last-scattering "surface" is just a circle. But that's because, in order to show this diagram, we have suppressed one spatial dimension. Instead of a circle, the last-scattering surface is actually a sphere. It's the surface around us, just the right distance away that photons scattering off of electrons for the last time, headed our way, are just getting here now.
A (Somewhat Boring) Map of the CMB
Penzias and Wilson had unwittingly stumbled upon the CMB. A key property about it they noticed, before they even knew it was the CMB, was its isotropy; no matter what seemingly empty piece of sky they pointed their telescope towards they got about the same amount of signal (or 'excess noise' as it appeared to them). We now know that it is isotropic to about one part in 1,000. This is such a high-degree of uniformity that a full-sky map of the CMB intensity looks completely uniform. The full-sky map below was made with data from the Differential Microwave Radiometer (DMR), an instrument launched on the COsmic Background Explorer (COBE) satellite in 1989. The high degree of uniformity of this map reflects the high degree of uniformity of the universe at the time of decoupling.
We refer to a quantity averaged over the whole sphere as a 'monopole.' Things get a tiny bit more interesting when we subtract this average intensity and look at what remains.

The CMB Dipole
The Earth moves around the Sun, which orbits the center of the Milky Way. The Milky Way galaxy itself is falling towards Andromeda and the Local Group of galaxies is falling toward the Virgo Cluster. It is no surprise then that we are moving with respect to the rest frame of the cosmic microwave background. Our relative motion induces a dipole pattern on the sky, as can be seen in the map below which has had the monopole subtracted from it. We see a dipole pattern, as well as contamination by some emission from our own galaxy clustered near a horizontal line that goes through the center of the map. Radiation in the Earth's direction of motion appears blueshifted and hence hotter, while radiation on the opposite side of the sky is redshifted and colder.
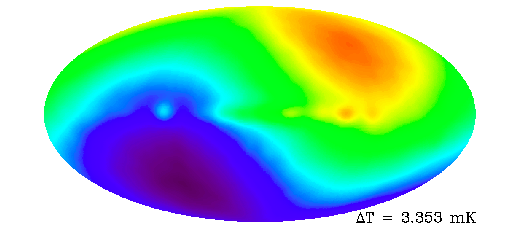
Figure 1.25.3: The CMB as mapped by the COBE satellite, after monopole subtraction. The dipole component is clearly visible. One can also see some emission from the plane of our own galaxy.
Beyond the Monopole and Dipole
With the monopole and dipole subtracted, the remaining variations in the temperature of the CMB are at the level of tens of microKelvin, reflecting small variations in conditions on the last-scattering surface. We will see such maps of the CMB in subsequent chapters and learn how we have used them to probe the dynamics of the primordial plasma. Before that though we will study the spectrum of the CMB, nature's best approximation to black body radiation.
Box 1.25.2
Exercise 25.1.1: Provide a 6 to 10-sentence summary of this chapter.


