6.2: The Force model

The Definition of Force 

Force is another type of vector which we will study extensively in this course. Forces will give us information about dynamics of objects: they will explain why some objects remain stationary and why other objects will move they way they do. A force is a push or a pull which describes an interaction between two objects. The word object is used here in a general sense to include any identifiable mass, which might be a particular volume of a fluid or a single electron, as well as ordinary objects such as a table, a book, or a car. The essential idea here is that forces do not exist in the absence of interacting objects. When you exert a "push" with your hand, there are two objects involved, your hand the object that you are pushing. A force is a vector quantity which describes both the strength of the push or pull (the magnitude of the force vector) and the direction of push and pull.  As we will see in the next few chapters both the strength and the direction of the force is essential to describing the dynamics of objects. Our understanding of just what a force is how how to use it to predict or explain motion will become sharper and more refined as we progress through the next couple of chapters.

Types of Forces 

An interaction can occur between objects that are in direct physical contact, as well as between objects that are widely separated in space. An example of the former is the force you apply on an object when you push it, or the force your bat exerts on a ball as you hit it into left field. An example of the latter is the force of gravity the Earth exerts on an orbiting satellite 200 miles above the surface of the Earth. The gravitational interaction between the Earth and other objects which may or may not be touching the Earth is said to be long range. The electric force between charged particles is another example of a long range force. The force resulting in an interaction continue to exist, even when there is no direct contact. This is distinctly different from the example of the bat and ball, once the ball is in the air after the bat has hit it, the bat no longer exerts a force on the ball. The type of forces such as that of the bat on the ball is often referred to as a contact forces, since there is no interaction or force if the bat and ball are not in physical contact (in a macroscopic sense).

Long Range Forces:

The electric and gravitational forces are said to be long-range forces, also known as fundamental forces. They are called fundamental since all other forces between macroscopic objects which will be describe shortly can be described in terms of fundamental forces (except for gravity) at a microscopic scale. Although the strength of the long-range forces decreases with distance, the interactions still exist and have profound effects even at large separation distances. The magnitude of the electric and gravitational force between two particles decrease as 1/r², thus, these two forces are often known as inverse-square law forces. In both cases, electric and gravitational, the force acts along the direction of the vector from one particle to the other. In addition, each force depends on a fundamental property of matter: electric charge and gravitational mass, respectively. These two forces are the manifestations of two of the four fundamental interactions: gravitational, electromagnetic, weak nuclear, and strong nuclear. We will cover the electromagnetic force is greater detail in Physics 7C.

We directly experience one of the fundamental forces all the time, the gravitational force. We know this force as the weight of an object. The weight of an object on the surface of the Earth is proportional to the mass of the object times acceleration due to gravity, g, having the value 9.80 m/s², which we often rounded to 10 m/s². We will mostly use the symbol, \(F_g\), for gravitational force which at the surface of the Earth is equal to:

\[F_g=mg\]

Contact Forces:

Recall in Physics 7A what happens when molecules get pushed very close together. The electrons then exert very large repulsive forces on each other. This is why substances resist compression. When we push on an object, it is the electrical forces between the electrons in the molecules of our skin and the electrons on the atoms at the surface of what we are pushing that are really doing the pushing. And it is the electrical forces holding molecules together that allow us to establish a tension in a stretched wire or cord.

So, we actually do experience electrical forces all the time. But because they are for the most part due to electrically neutral molecules interacting with each other, the net forces are “short range” and are not given by our simple formula. We often describe these electric forces as contact forces. In other words, the forces that electrical neutral objects exert on each other when they are brought into close proximity really are electric forces, but they are very short range, and are not described by the inverse-square law. We often categorize these laws based on the type of interaction that is occurring macroscopically.

Here are basic description of some of these forces:

- normal force: a repulsive "push" force due to physical contact of an object with a surface which always acts perpendicular (which is the meaning of the word "normal") to that surface. We often use the symbol, \(F_N\), for this force.

- tension force: an attractive "pull" force which is transmitted through a string or rope. We often use the symbol, \(T\) or \(F_t\) for this force.

- friction: a force which acts between two objects parallel to their surfaces, and acts in the direction opposite their motion (known as kinetic friction) or in the direction opposite their intended motion (known as static friction). Kinetic friction explains why a toy car when pushed on a rough surface will eventually come to a stop. The expression for kinetic friction which is determined experimentally is given by:

\[F_k= \mu_k F_N\]

where \(\mu_k\) is the coefficient of kinetic friction and \(F_N\) is the normal force. The coefficient of kinetic friction depends of the nature of the materials that are rubbing against each other. The more slippery the materials are, the less is the effect of friction, resulting in a smaller coefficient of kinetic friction. The normal force also plays a role on how much the two materials are rubbing against each other. The harder you push perpendicular to the two surfaces, the harder it will be for them to slide relative to each other. A heavier object, resulting in a larger normal force, will stop faster when moving on a surface than a lighter object.

Static friction explains why a car parked on a slopped hill does not simply roll down, or why a heavy object doesn't budge when pushed. For static friction the applied force need to reach a critical magnitude before the friction is overcome, and the object starts to move. The expression for static friction is:

\[F_s\leq \mu_s F_N\]

where \(mu_s\) is the coefficient of static friction and \(F_N\) is the normal force. When an object is stationary, all forces need to be balanced. If you lightly push on a heavy object and it does not move, then the force is static friction is equal to your push. If you now push a little harder but the object still does not move, then the force of static friction is now larger than before to balance with the stronger push. The maximum value that static friction can have is \(F_s =\mu_s F_N\). The coefficient of static friction is typically larger than the coefficient of kinetic friction. It is more difficult to get the motion started than to keep the motion going.

- air friction or drag force: when an object moves through a gas or liquid there are there are drag or viscous forces retarding the motion of the object. These forces act in the direction opposite to the velocity of an object and are zero is the object is stationary. When a parachute is falling down or a car moves on a highway at a high speed, air exerts a drag force, sometimes called air friction.

 

- spring force: Robert Hooke (a contemporary of Isaac Newton) discovered in 1676 that the force exerted by many stretched springs is proportional to the elongation or compression of the spring and in the opposite direction to the elongation or compression. The constant of proportionality depends on the way the particular spring is made (its material, size, number of coils, etc.). We used this model for springs extensively in Physics 7A. In equation form we express the force exerted by a spring, known as Hooke's Law, as

\[\vec F_s=-k\Delta \vec x\]

where \(k\) is the spring constant and \(\Delta \vec x\) is the displacement away from equilibrium. We write Hooke's law in vector form order to stress the relationship between the direction of force and displacement. Whether the spring is stretched or compressed the vector \(\Delta \vec x\) points away from equilibrium, while the spring force always points in the opposite direction, toward equilibrium, due to the minus sign in the equation. Note the "\(\Delta\)" in the expression for displacement does not correspond to the more common "before and after" application of the symbol.  This "\(\Delta\)" stresses that it is the distance from equilibrium that is measured. If the equilibrium position is at some distance \(x_o\), then \(\Delta \vec x=\vec x-\vec x_o\), where \(\vec x\) is position of the spring after it have been stretched or compressed.

Newton's First Law 

Before Isaac Newton, arguably the greatest scientist of all time, came along and changed the view of nature forever, the belief established by thinkers such as Aristotle was that motion required forces. In other words, ancient (pre-Newtonian) understanding of motion was that for an object to move a force needs to be acting on it and that eventually everything comes to a stop. Newton claimed the opposite, that for an object to stay at rest or to remain moving with a constant velocity (constant speed moving in a straight line) no total force can be acting on it. This statement is known as Newton's First Law.

Newton's 1st Law of Motion

Objects at rest stay at rest and objects moving in a straight line at a constant speed continue moving this way unless acted upon by an external total force.

Let us think carefully about the implications of Newton's First Law by thinking about a specific scenario. When you are standing on the floor in an airport terminal and then one hour later when you are standing in the aisle of a jet plane going 500 miles per hour with no turbulence, you experience the same sensations on your body. This illustrates a fundamental aspect of the 1st Law. If the total net force is zero on you when standing on the floor of the airport terminal, and the net force on you is also zero when on the jet traveling at a constant speed with respect to the ground, the effect is the same: no change in motion. From your perspective you are standing still on the ground and standing still on the airplane. But from another person’s perspective at the airport, when you are on the airplane you moving at a constant 500 miles per hour. Evidently, being motionless and moving with a constant velocity are the same thing with respect to how forces work. Because forces work this way, we can turn moving at a constant velocity to being motionless by switching to reference frame that is moving with the same velocity with respect to the original reference frame.

The word total force (also called net force) in the statement above has very important implications. Newton's First Law does not claim that no forces can be acting on the object for it to remain at rest or moving at constant velocity, but rather the total force acting on the object must be zero. A book which is stationary on a table has a force of gravity acting on it. Thus, Newton's First Law implies that there must be another force acting on the book that must balance the force of gravity. This force is the normal force of the table pushing back on the book. In other words, the fundamental aspect of Newton's First Law is that if all the forces acting on an object, both contact and long-range forces, are balanced and the total force is zero, then all of those forces acting together have no effect on the object. It is as if there are no forces acting on the object. The effect of all forces acting on a particular object can be represented by a single vector called the total force or the net force which is defined as the sum of all forces acting on that object:

\[\vec F_{net}=\Sigma\vec F\]

Mathematically, Newton's First Law can be stated as:

\[\textrm{if}~~\vec F_{net}=0, \textrm{then}~~\Delta\vec v=0\label{1stLaw}\]

The quantity  \(\Sigma\vec F\) is a vector sum, since the individual forces acting on the system are vector quantities. The net force is not a physical force due to a particular interaction with another object acting on the system, but rather it is the effect of all the forces acting on our system. Because of this lack of connection to a particular interaction, net force is a rather abstract concept, but one that turns out to be very useful.

Newton's First Law describes situations when all the forces acting on an object are balanced. There are two complementary ways of applying the 1st Law. If we know that there is no change in motion, then we know that the forces acting on the object must be balanced. If we know all but one of the forces, we can solve for the the magnitude and direction of the unknown force. The second way to use the 1st Law is to add up the known forces to see if they balance. If they do, than there cannot be a change in motion of the object.

The sum over all forces \(\Sigma\vec F=0\) is a vector quantity which can re-written in terms of its components, assuming forces act in only two-dimensions, as:

\[\Sigma\vec F=(\Sigma F_x,\Sigma F_y)=(0,0)\]

The equation above implies that for the net force to be zero, the sum components of all the forces in the x-direction must be zero, as well as in the y-direction. In other words, when balancing forces, you are really trying to solve two independent equations (if you are working in 2D), on the x-direction and another in the y-direction. Technically, the equation above can be written as a set of two independent equations:

\[\Sigma F_x=0\]

\[\Sigma F_y=0\]

Let us look at an example shown below in Figure 6.2.1, where we would like to analyze a box which is being pushed and kept stationary against the wall by a person in terms of Newton's First Law. All forces acting on a box are labeled. 

Force notation

In order to stress that two objects are interacting when there is a force present an "on-by" notation is often used when labeling forces. So if a force is acting on object A and is being exerted by object B we write this as: \(F_\textrm{on object A by object B}\).

Figure 6.2.1: Balanced Forces

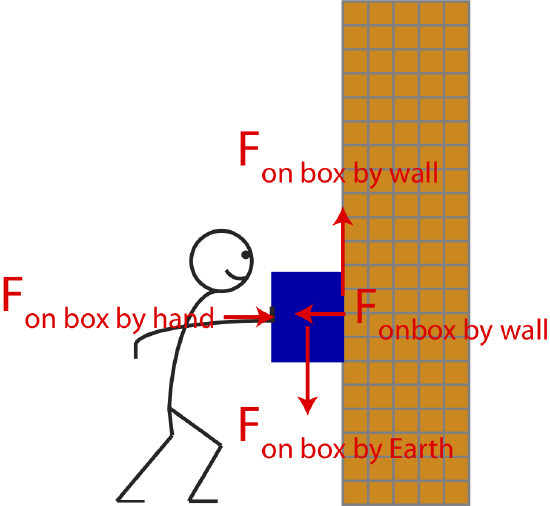
Once you define a system, in this case a box, in order to figure out which forces are acting on the system you need to identify all the objects that the system is in direct physical contact with and if any long-range forces involved. If the system is in a gravitational field (on Earth, for example) and the mass of the system is not negligible, then we always must include the long-range gravitational force acting directly down toward the surface of the Earth. In Figure 6.2.1, the gravitational force is labeled as \(F_{\textrm{on box by Earth}}\) to stress the fact that it represents an interaction between two objects, the box and Earth. The "on box" is due to our system being the box, and "by Earth" is the object which is exerting a force on our system. As you get more comfortable with working with forces, you can abbreviate the gravitational forces acting on a system as simply \(F_g\). Since the box is stationary (not slipping down), Newton's First Law tells us that there has to be an equal an opposite force pointing up. The box is in physical contact with the wall, which is exactly what provides the force holding the box. It is a horizontal force between two surfaces (the box and the wall), which we defined as the force of friction. The notation \(F_{\textrm{on box by wall}}\) is again to stress that it is a contact force due to the interaction between the box and the wall, but it can be abbreviated as the frictional force \(F_f\).  Using this notation, we balance the two forces by summing them to zero. If we defining up as the positive direction then the net force in the y-direction is:

\[F_f-F_g=0,\]

resulting in \(F_f=F_g\). The frictional force generated by wall on the the box when in contact must point up and have the same magnitude as the gravitation force on the box by the Earth.

In the x-direction, the person is pushing the box with their hand, so there is a force on the box by the hand pointing to the right. To balance this force, there must be an force pointing in the opposite direction. Since the box is touching the wall, this force is by the wall and is perpendicular to the surface, which we defined as the normal force. The notation for this normal force can be abbreviated as \(F_N\), but again the notation \(F_{\textrm{on box by wall}}\) is to stress that this force is due to the interaction of our system with the wall. Defining the positive x-direction as the one pointing to the right and balancing forces in the x-direction we get:

\[F_{\textrm{on box by hand}}-F_N=0,\]

resulting in \(F_{\textrm{on box by hand}}=F_N\), so the normal force needs to be equal and opposite to the push force by the person.

As seen in this example, both the perpendicular (the normal force) and parallel (friction) forces arise from the same interaction, the box with the wall. Thus, these seemingly two separate forces are just the parallel and the perpendicular complements of one force, the force exerted by the wall on the box. Often, using the words "normal" and "friction" are abstract since they do not directly tell you about the particular interaction. You should always start your force analysis by first considering the physical objects which are interacting with your system, either by direct contact (like the wall) or at a distance (like the Earth).

Example \(\PageIndex{1}\)

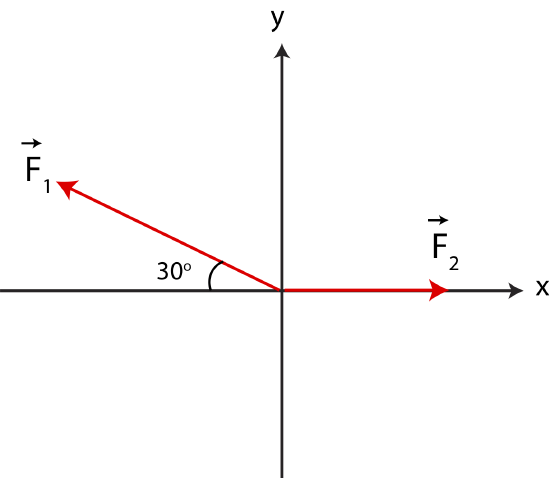
An object is moving with a speed of 5m/s in the positive y-direction while three forces are acting on it. Two of the forces are shown in the figure below. The magnitude of \(\vec F_1\) is 16 N and the magnitude of \(\vec F_2\) is 10 N. Find the magnitude and direction of \(\vec F_3\).

Solution

Since the object is moving at a constant velocity the three forces must add up to zero:

\[\vec F_{net}=\vec F_1+\vec F_2+\vec F_3=0\]

This implies that:

\[\vec F_3=-\vec F_1-\vec F_2\]

Expressing each force by components we get:

\[\vec F_1=16N(-\cos 30^{\circ},\sin 30^{\circ})=(-13.86,8)N\]

\[\vec F_2=(10,0)N\]

Plugging into the expression for \(\vec F_3\):

\[\vec F_3=-(-13.86+10,8+0)=(3.86,-8)\]

The magnitude of the vector \(\vec F_3\) is:

\[|\vec F_3=\sqrt{3.86^2+8^2}=8.88 N\]

And the angle:

\[\theta=\arctan\Big(\frac{8}{3.86}\Big)=64.2^{\circ}\]

in the southeast direction.

Newton's Second Law 

Newton's First Law is a special case of Newton's Second Law which describes what happens when the net force acting on the system is not zero. It states that when the net force acting on an object is not zero, then it will experience an acceleration in the direction of the net force.

Newton's 2nd Law of Motion

The net force acting on an object is equal to its mass times its acceleration.

Mathematically, Newton's Second Law is written as:

\[\vec F_{net}=m\vec a\label{2ndLaw}\]

As we described in Section 6.1 acceleration is a vector which describes the rate of change of velocity, or change of motion. Some examples of the influence of this non-zero net force could be an stationary object starting to move, a moving object speeding up, slowing down, or coming to a rest, of a moving object changing its direction even while its speed is staying constant. If there is no net force acting on the system, Equation \ref{2ndLaw} states that acceleration is zero, which directly implies that \(\Delta\vec v=0\) and we recover Newton's First Law as given in Equation \ref{1stLaw}.

Although Equation \ref{2ndLaw} is rather simple mathematically, its physical meaning is often misinterpreted. The equation is often read as: "an object which is accelerating is carrying a force which is equal to the object's mass times its acceleration, and then will exert this force if it interacts with another object". This way to interpreting Newton's 2nd Law is completely wrong. To help resolve this interpretation it more physical to think about Equation \ref{2ndLaw} in reverse: "an object which has a net external force acting on it will experience an acceleration which is equal to this net force divided by its mass". In other words, the common misinterpretation is due to cause and effect being reversed: it is not that an accelerating object produces a net force, but rather a net forces results in an acceleration. Thus, it is better to re-write Newton's Second Law as: 

\[\textrm{if}~~\vec F_{net}\neq 0, \textrm{then}~~\vec a=\frac{\vec F_{net}}{m}\label{2ndLaw-exp}\]

Having the 2nd Law written as above also makes it more obvious to see that the 1st Law, as given in Equation \ref{1stLaw}, is just a special case of the 2nd law when the net force is zero. We will going into more details of applying Newton's 2nd Law in later chapters.

Newton's Third Law 

As we start to understand forces in greater details, it is important to remind ourselves that the starting point is a very important aspect that forces come in pairs, which is a direct consequence of the fact that forces describe interactions between two objects.  To have an interaction, we must have two objects that are interacting. Suppose object A is interacting with object B. Focusing on object B, we would say that object A exerts a force on object B. Alternatively, focusing on object A, we would say object B exerts a force on object A. These two forces, associated with the same interaction between the same two objects must be related to each other. But how are they related? It turns out these forces are equal and opposite. This is known as Newton's Third Law of motion. Mathematically, the two forces between two interacting objects, object A and object B point in opposite directions and the magnitude of the force that object A exerts on object B has the same magnitude as the force that object B exerts on object A.

\[\vec F_{\textrm{on B by A}} = -\vec F_{\textrm{on A by B}}\label{3rdLaw}\]

In words, this relationship can be expressed as, “If object A exerts a force on object B, then object B exerts a force equal in magnitude and opposite in direction on object A”.

The effect of the interaction on each of the objects, however, does not have to be the same, and usually it is not the same. The effect of the interaction depends on other properties of the specific object, such as its mass and its motion prior to the interaction. For example, when a bug collides with the windshield of a moving car, Newton's Third Law tells us that the car and the bug experience the same magnitude of force in opposite direction, but the effect on the motion of the two objects is obviously very different. This is an important distinction: the interaction is always the same with respect to the two objects, but the effect that the interaction has on each of the two objects does not have to be the same and usually is not. It is very important to keep this distinction in mind when thinking about forces. Newton's Second Law is what gives us an answer about why the effect is different even though the forces are the same. The car which has a much greater mass compared to a bug, will experience a much smaller acceleration for the same magnitude of force. Thus, the change of motion of the car will be negligible, while the bug will experience a much greater acceleration due to its tiny mass.

Figure 6.2.2 below shows an example of a Third Law pair, which describes the two forces involved in one interaction. In this example, a person exerts a force on the wall by pushing on it with their hand, labeled as \(F_{\textrm{on wall by hand}}\) and drawn with an arrow pointing to the right, toward the wall. Newton's Third Law tells us that the wall must exert a force on the hand with the same magnitude as the push by the hand by in the opposition direction. This force is labeled in the figure as \(F_{\textrm{on hand by wall}}\) and drawn with an arrow which has the same length as \(F_{\textrm{on wall by hand}}\) but in the opposite direction, toward the hand.

Figure 6.2.2: Third Law Pair

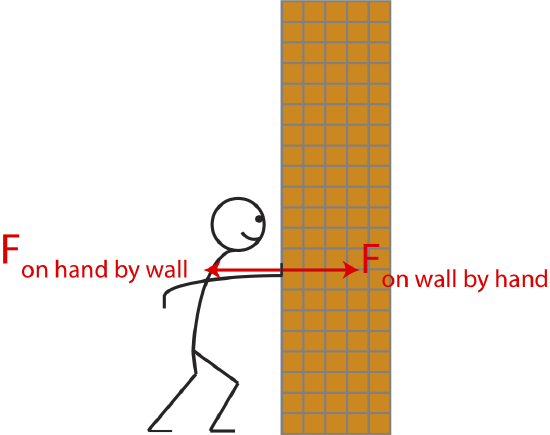
A Third Law pair can always be recognized by looking at the "on by" notation, with the objects in this notation are flipped, a 3rd law pair is recognized. This is another reason to stick with the "on by" notation when analyzing forces, since it is an clear way to track which object is experiencing the force and which object is exerting it.

Here is another common misinterpretation that often occurs when thinking about Newton's Third Law this time, "since for every force there is an equal and opposite force which is present, how can anything ever move since all the forces always balance?". It is important to distinguish between forces exerted by a particular object on other objects, and the forces those other objects exert on the original object. Only forces acting on an object affect that object. Forces that an object itself exerts on other objects do not affect itself. Therefore, when applying Newton's 1st and 2nd laws we only consider forces on the object whose motion we are analyzing, and ignore all the forces that object exerts on other objects. It is sometimes easy to confuse the 1st and 3rd laws, especially when there are two forces acting on an object. The pairs of forces that balance each other in the First Law act on the same object, so they cannot possibly be Third Law force pairs, even though they are equal and point in opposite directions.

The wall in Figure 6.2.2 does not move not because the two forces shown in the figure which describe the 3rd law pair balance, but because the wall is attached to the floor, and the floor exerts an force on the wall (static friction) in the opposite direction of the push on the wall. These two forces (on the wall by the hand and on the wall by the floor) balance and prevent the wall from moving due to Newton's First Law. 

• Authors of Phys7A (UC Davis Physics Department)