8.4: Statistics of Identical Particles

Multiple Particles in the Same Potential Well

The increased degeneracy introduced by the additional degree of freedom that comes from spin addresses the number of unique states for the same energy level of a single, but where the addition of this additional quantum number really gets interesting is when we put several particles together into a common potential. Again, we continue to assume that the particles do not interact with each other.

Let's take as an example a one-dimensional infinite square well (we aren't very creative, this is the first example we use for everything). Let's place five identical particles into this "box," such that they reach an energy eigenstate. [Keep in mind we are talking about a multi-particle quantum state here.] The question we want to answer is, what is the ground state energy of this configuration?

It turns out that we can't answer this without knowing what types of particles we are putting into the box. We know from our separation of variables work (and frankly, just from energy conservation), that the total energy of the multi-particle state will be the sum of the energies of the individual particles, so we might think that the lowest total energy occurs when each particle is in its individual ground state. But not so fast!

What if the particles are electrons? These are spin-\(\frac{1}{2}\) fermions, which means that there is zero probability of having two of them with the same quantum numbers. There are two quantum numbers present here – one for the single dimension, and one for the intrinsic spin degree of freedom. So we can "fit" two electrons into their lowest individual energy states if they have opposite spins, but we can't get the third electron into the ground state without violating the exclusion principle, so this third electron must reside in its first excited state. We can also get a fourth electron into the first excited state, but then the fifth must be in the second excited state.

If the particles are bosons, then no problem, all three particles can reside in the ground state at once, and that will be the lowest total energy state for the system. Have we solved this problem for all particles? No! Recall that not all fermions are spin-\(\frac{1}{2}\); higher spin quantum numbers are also possible. If we use spin-\(\frac{3}{2}\) fermions, then there are four different spin states available: \(m_s = \pm \frac{1}{2},\; \pm\frac{3}{2}\). With four different states available for a single energy level, there is plenty of room to fit all of these fermions in their individual ground states.

Figure 8.4.1 – Multi-Particle Ground State According to Particle Spin

Revising Boltzmann – The Statistics of Identical Particles

The quantum mechanics of identical particles has a profound effect on statistical physics. In 9HB, we encountered the Boltzmann distribution and applied it to computing entropy from multiplicities of microstates. The whole subject of the Boltzmann distribution boiled down to this: Give a collection of particles a certain total amount amount of energy. Each particle gets its own share of that energy, and those "shares" are distributed through a wide range of values. We can compute the probability (when the collection reaches equilibrium) that any given particle will get an amount of energy in a given infinitesimal range, by using the fact that the distribution will be at equilibrium when the maximum multiplicity is reached.

But here is the rub: The Boltzmann distribution assumes that all of the particles are distinguishable. In the non-quantum world in which Boltzmann operated, the motions of all particles could in principle be tracked. We can see why things change by considering 4 particles, this time all in a one-dimensional harmonic oscillator potential. We wish to compute the multiplicity of the state where the system has a total energy of \(8E_o\), where of course \(E_o=\hbar\omega_c=\hbar\sqrt\frac{\kappa}{m}\). There are only two ways that the energies of these particles can add up to \(8E_o\): Three particles in the ground state, and one particle in the second-excited state, or two particles in each the ground state and first excited state:

\[\begin{array}{l}3\cdot E_o + 1\cdot E_2 = 3\cdot \frac{1}{2}\hbar\omega_c+1\cdot \left(2+\frac{1}{2}\right)\hbar\omega_c=4\hbar\omega_c=8E_o \\ 2\cdot E_o + 2\cdot E_1 = 2\cdot \frac{1}{2}\hbar\omega_c+2\cdot \left(1+\frac{1}{2}\right)\hbar\omega_c=4\hbar\omega_c=8E_o \end{array}\]

Let's start by counting the multiplicity that these available states provides for distinguishable particles (Boltzmann statistics). We can place 4 distinguishable particles into energy levels such that their total energy adds up to \(8E_o\) in ten different ways:

Figure 8.4.2 – Combinations of Distinguishable Particles

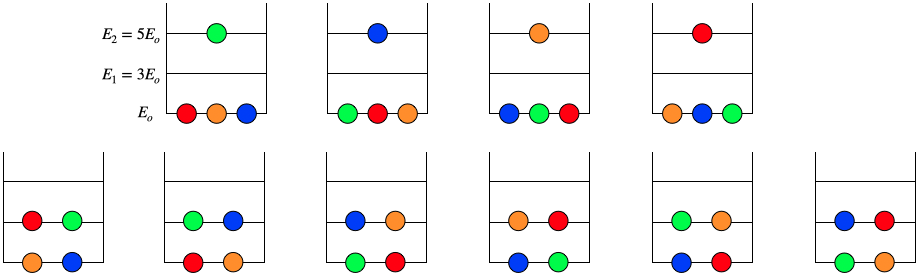
If we wanted to know (say) the probability of selecting a particle at random in the ground state, we would divide the number of particles in the ground state by the total number of possibilities, and find it equals 0.6. When we increase this to a very large number of particles, we get the Boltzmann probability of finding a particle at energy \(E_n\) for a collection of particles at temperature \(T\):

\[P\left(E_n\right) \propto \frac{1}{e^{E_n/k_BT}}\]

Now let's remove the condition that the particles are distinguishable. We'll look at the case for bosons first. When we make all the "particles" in our diagram the same color, we get only two different set-ups:

Figure 8.4.3 – Combinations of Indistinguishable Bosons

Here we see that the probability of randomly selecting a particle in the ground state is different from the case with distinguishable particles – it is 0.625. We won't go into the combinatorics to prove it here, but for a large number of particles, the difference between the probabilities for indistinguishable bosons (called Bose-Einstein statistics) and the distinguishable particle case comes out to be an extra "\(-1\)" term in the denominator:

\[P_{BE}\left(E_n\right) \propto \frac{1}{e^{E_n/k_BT}-1}\]

[Note: This and the case to follow have been slightly over-simplified to emphasize the effect of the change of statistics in the denominator, with the removal of a number called the chemical potential. In the case of a "photon gas" (which satisfies Bose-Einstein statistics, as photons are spin-1), this chemical potential is zero, and this expression is accurate.]

Okay, what about the case of spin-½​​​​ fermions? In this case, we know that no more than two can occupy the same energy state, thanks to the exclusion principle. This gives exactly one configuration for our 4-particle case:

Figure 8.4.4 – Combinations of Indistinguishable Spin-½​​​​ Fermions

Now the probability of randomly selecting a particle in the ground state is different from the previous two cases – it is now 0.5. For a large number of particles, the difference between the probabilities for indistinguishable fermions (called Fermi-Dirac statistics) and the distinguishable particle case comes out to be an extra "\(+1\)" term in the denominator:

\[P_{FD}\left(E_n\right) \propto \frac{1}{e^{E_n/k_BT}+1}\]