1.12: The Evolution of Mass-Energy Density and a First Glance at the Contents of the Cosmos
( \newcommand{\kernel}{\mathrm{null}\,}\)
We've seen that the rate of change of the scale factor depends on the mass density ρ. In order to determine how the scale factor evolves with time, we thus need to know how the density evolves as the scale factor changes. In this section we'll work that out for three cases. The first two are collections of particles: 1) non-relativistic particles, by which we mean those with rest-mass energy (mc2) much greater than kinetic energy, and 2) relativistic particles, by which we mean particles with much greater kinetic energy than rest-mass energy. The former we call "matter" and the latter we call "radiation." The third one is much more exotic: a cosmological constant.
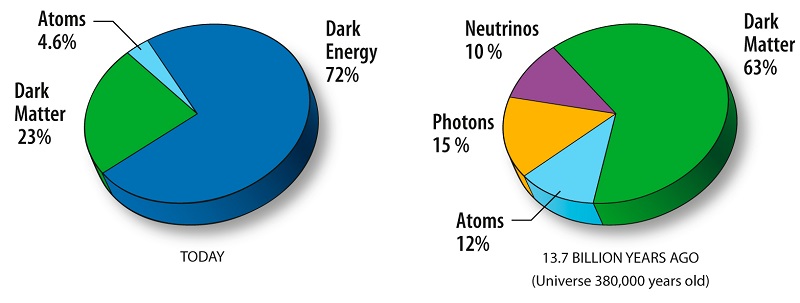
These are the three categories we need to describe the evolution of mass-energy density for all the significant components of the standard cosmological model. The relative contributions of these components to the total mass-energy density today, and over 13.7 billion years ago, are shown in the graphic to the right, as cosmologists have estimated them using data from NASA's Wilkinson Microwave Anisotropy Probe (WMAP) satellite. We'll call these components out as we consider Matter, Radiation, and the cosmological constant.
Matter
Let's begin by thinking about how the energy density of the gas in this room would evolve under expansion. Before we even get to that though, let's compare the kinetic energy of a typical Nitrogen molecule in the room to its rest-mass energy. The kinetic energy is roughly given by kBTroom≃1/40eV where eV is a unity of energy called an electron Volt equal to the kinetic energy that an electron gains crossing a potential difference of 1 Volt. To get the rest mass, note that Nitrogen's most abundant isotope has 7 protons and 7 neutrons, and the molecule is two Nitrogen atoms so its mass is about 28 times the mass of the proton. The proton mass is almost 1×109eV/c2, so the Nitrogen molecule rest mass energy is roughly mc2=28×109eV. You can see that its rest mass energy is much greater than its kinetic energy.
In thinking about the energy density of a gas of particles we need to keep track of the rest mass energy and the kinetic energy. However, for non-relativistic particles, those moving much more slowly than the speed of light, like the particles in the gas in this room, the kinetic energy is tiny compared to the total energy and we can ignore it. That makes our calculation very straightforward. Expansion will dilute the number of particles by the increase in volume.
Box 1.12.1
Exercise 12.1.1: For a collection of particles all of the same mass, m, their energy density is given by:
ρc2=mnc2
where n is the number density of the particles. In your own words, argue that n∝a−3, and hence ρ∝a−3. It might be helpful to track a collection of the particles in a cubic volume over time. Have the volume expand so that it always contains those particles and no others. What happens to the total energy in the box as the scale factor increases? What happens to the volume of the box as the scale factor increases?
In the WMAP graphic, "Atoms" and "Dark Matter" are both forms of Matter. Atoms are just the usual matter we are familiar with from everyday life. They are the elements of the periodic table. We actually don't know what the dark matter is. But there are many different observations that can be most easily understood if we assume there is a significant amount of some unknown, not-yet-detected, type of non-relativistic particle that contributes more to the mass-energy of the universe than atoms do by a factor of 5.
Radiation
For any collection of particles the energy density is given by ρc2=ˉEn where ˉE is the average energy of the particles. For massless particles, E=pc so E∝1/a for each particle so we also know that ˉE∝1/a. As long as particles are not being destroyed, just like for the non-relativistic particles, n∝1/a3. Putting this together, for relativistic particles we have ρ∝a−4. In the WMAP graphic, Photons and Neutrinos both count as radiation. Photons are the clearest case since, as they have no mass, their kinetic energy is always much greater than their rest-mass energy. Neutrinos are subatomic particles that do have a small amount of mass, but for much of the history of the universe we expect that these particles have much greater kinetic energy than rest-mass energy and hence qualify as radiation.
The Cosmological Constant
It is a logical possibility, consistent with Einstein's equations, that there is an energy density associated with space itself; i.e., a certain amount of energy in every cubic centimeter, an amount that does not change with time. Thus, by definition, for a cosmological constant the mass-energy density is independent of the scale factor: ρ∝a0. As we will see, there is evidence supporting the existence of a non-zero cosmological constant. Einstein considered this possibility early on as a means to explain why the universe is static (as he thought it was), rather than expanding or contracting, when he introduced the cosmological constant via an additional term in his field equations.
Einstein's reasons for introducing the cosmological constant turned out to be unfounded. In 1929 Edwin Hubble reported his inferences of recession velocity and distance for a set of (relatively nearby) galaxies, that showed a roughly linear trend of increasing velocity with distance, just as one would expect from a uniform expansion. Einstein missed the opportunity to predict the discovery of the expansion of the universe, a missed opportunity he referred to as his greatest blunder.
The cosmological constant though has refused to die. There are two reasons for this. The first is due to the fact that if one tries to calculate, using quantum field theory, the energy density that is in every cubic centimeter of space from the zero-point energy of all the quantum fields, one gets an enormously large energy density, larger than observational limits by about 10120. This huge embarrassment of modern physics is called ``the cosmological constant problem.''
The second is that over the past twenty years strong evidence has emerged that the dominant contribution to the mean energy density of the universe in the current epoch is something that is behaving a lot like a cosmological constant. As we will see soon, the observational evidence comes from inferences of the relationship between distance and redshift that indicate the expansion rate is accelerating; i.e., that ¨a>0. Radiation and matter lead to deceleration, while a cosmological constant can produce acceleration (as you will shown in the Box below). The first claims of acceleration from redshift-distance inferences were published in 1998, and were based on observations of Type 1a supernovae. Three of those leading these efforts were awarded the Nobel Prize in Physics in 2011 for their work. The "Dark Energy" label in the WMAP graphic is a more general term than "cosmological constant." It is the general name for the component of the universe that is causing acceleration in the current epoch. A cosmological constant is a very specific kind of dark energy.
Box 1.12.2
Exercise 12.2.1: Show that for an expanding universe with k=0 and only matter or radiation that ¨a<0. Start from the Friedmann equation. (Tip: you do not need to actually calculate ¨a; instead, you can show that ˙a will decrease as a increases. This may be easier).
Exercise 12.2.2: Show that for an expanding universe with k=0 and only a cosmological constant that ¨a>0. Start from the Friedmann equation.
Summary
The universe has components that change with scale factor in three different ways:
- Non-relativistic matter, aka "Matter" has a mass-energy density ρ∝a−3,
- Relativistic matter, aka "Radiation", has a mass-energy density ρ∝a−4, and
- Dark Energy, whose mass-energy density evolves much more slowly; for the specific case of a cosmological constant ρ∝a0.
These different behaviors lead to them having different mixes over time in the history of the universe, and explain the differences in the two pie charts in the WMAP graphic. There are still neutrinos and photons around in the current epoch, but their contributions are just so small they have not been included in the graphic. Their steeper dependence on a means that at earlier and earlier times they contributed a greater and greater share of the total mass-energy budget.
HOMEWORK Problems
Note: Unless directed otherwise, in these first three problems assume that k=0 and ρ∝a−3.
Problem 1.12.1
In the standard model of cosmology the universe has gone through at least three different "eras." These are the radiation-dominated era, the matter-dominated era and the dark energy-dominated era. In the radiation-dominated era, for example, more mass-energy comes from radiation than from matter or dark energy. Think about how energy density evolves with scale factor for each of these components and identify which era was first, which second and which third (that is, specify the temporal ordering). Make a sketch of log(a) vs. log(ρ) for each of the components, all on the same graph. On the graph indicate the ranges of scale factor for each of the three eras. I am only looking for something qualitatively correct here. Do not worry about having the right value of the scale factor for the transitions, just have the eras in order. Your axes need not have any numbers on them, but do indicate where on the log(a) axis today is.
Problem 1.12.2
From the time referred to in the pie chart to the right in the WMAP graphic, to "TODAY", the universe has expanded by a factor of about 1100. Given that information, and assuming that over this time period there has been negligible destruction or creation of photons, atoms, and dark matter, about what fraction of the mass-energy density today is contributed by photons?
Problem 1.12.3
Later we will study the epoch of "big bang nucleosynthesis" (BBN) when most of the Helium in the universe was created, as well as trace amounts of some other light elements. The scale factor was about one million times smaller in this epoch than it was at the time referred to in the pie chart on the right in the WMAP graphic. Assuming that neutrino mass can be ignored between these two different times, what is the ratio of radiation mass-energy density to matter mass-energy density at the epoch of BBN?


