17.4: Using Spectra to Measure Stellar Radius, Composition, and Motion
- Page ID
- 3724
Learning Objectives
By the end of this section, you will be able to:
- Understand how astronomers can learn about a star’s radius and composition by studying its spectrum
- Explain how astronomers can measure the motion and rotation of a star using the Doppler effect
- Describe the proper motion of a star and how it relates to a star’s space velocity
Analyzing the spectrum of a star can teach us all kinds of things in addition to its temperature. We can measure its detailed chemical composition as well as the pressure in its atmosphere. From the pressure, we get clues about its size. We can also measure its motion toward or away from us and estimate its rotation.
Clues to the Size of a Star
As we shall see in The Stars: A Celestial Census, stars come in a wide variety of sizes. At some periods in their lives, stars can expand to enormous dimensions. Stars of such exaggerated size are called giants. Luckily for the astronomer, stellar spectra can be used to distinguish giants from run-of-the-mill stars (such as our Sun).
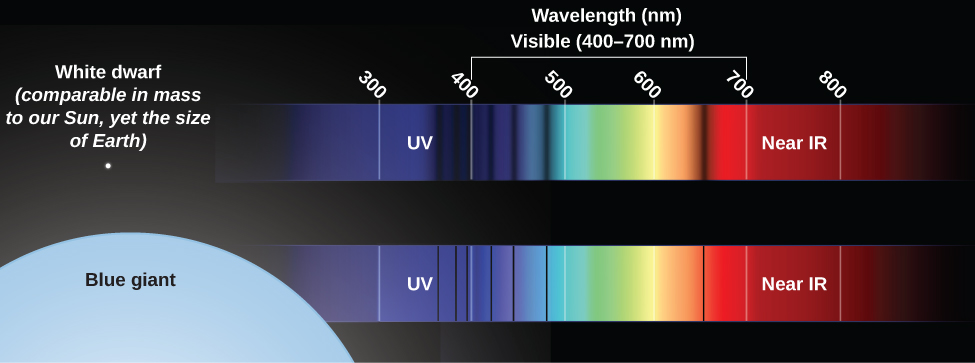
Suppose you want to determine whether a star is a giant. A giant star has a large, extended photosphere. Because it is so large, a giant star’s atoms are spread over a great volume, which means that the density of particles in the star’s photosphere is low. As a result, the pressure in a giant star’s photosphere is also low. This low pressure affects the spectrum in two ways. First, a star with a lower-pressure photosphere shows narrower spectral lines than a star of the same temperature with a higher-pressure photosphere (Figure \(\PageIndex{1}\)). The difference is large enough that careful study of spectra can tell which of two stars at the same temperature has a higher pressure (and is thus more compressed) and which has a lower pressure (and thus must be extended). This effect is due to collisions between particles in the star’s photosphere—more collisions lead to broader spectral lines. Collisions will, of course, be more frequent in a higher-density environment. Think about it like traffic—collisions are much more likely during rush hour, when the density of cars is high.
Second, more atoms are ionized in a giant star than in a star like the Sun with the same temperature. The ionization of atoms in a star’s outer layers is caused mainly by photons, and the amount of energy carried by photons is determined by temperature. But how long atoms stay ionized depends in part on pressure. Compared with what happens in the Sun (with its relatively dense photosphere), ionized atoms in a giant star’s photosphere are less likely to pass close enough to electrons to interact and combine with one or more of them, thereby becoming neutral again. Ionized atoms, as we discussed earlier, have different spectra from atoms that are neutral.
Abundances of the Elements
Absorption lines of a majority of the known chemical elements have now been identified in the spectra of the Sun and stars. If we see lines of iron in a star’s spectrum, for example, then we know immediately that the star must contain iron.
Note that the absence of an element’s spectral lines does not necessarily mean that the element itself is absent. As we saw, the temperature and pressure in a star’s atmosphere will determine what types of atoms are able to produce absorption lines. Only if the physical conditions in a star’s photosphere are such that lines of an element should (according to calculations) be there can we conclude that the absence of observable spectral lines implies low abundance of the element.
Suppose two stars have identical temperatures and pressures, but the lines of, say, sodium are stronger in one than in the other. Stronger lines mean that there are more atoms in the stellar photosphere absorbing light. Therefore, we know immediately that the star with stronger sodium lines contains more sodium. Complex calculations are required to determine exactly how much more, but those calculations can be done for any element observed in any star with any temperature and pressure.
Of course, astronomy textbooks such as ours always make these things sound a bit easier than they really are. If you look at the stellar spectra such as those in Figure \(17.3.3\) in Section 17.3, you may get some feeling for how hard it is to decode all of the information contained in the thousands of absorption lines. First of all, it has taken many years of careful laboratory work on Earth to determine the precise wavelengths at which hot gases of each element have their spectral lines. Long books and computer databases have been compiled to show the lines of each element that can be seen at each temperature. Second, stellar spectra usually have many lines from a number of elements, and we must be careful to sort them out correctly. Sometimes nature is unhelpful, and lines of different elements have identical wavelengths, thereby adding to the confusion. And third, as we saw in the chapter on Radiation and Spectra, the motion of the star can change the observed wavelength of each of the lines. So, the observed wavelengths may not match laboratory measurements exactly. In practice, analyzing stellar spectra is a demanding, sometimes frustrating task that requires both training and skill.
Studies of stellar spectra have shown that hydrogen makes up about three-quarters of the mass of most stars. Helium is the second-most abundant element, making up almost a quarter of a star’s mass. Together, hydrogen and helium make up from 96 to 99% of the mass; in some stars, they amount to more than 99.9%. Among the 4% or less of “heavy elements,” oxygen, carbon, neon, iron, nitrogen, silicon, magnesium, and sulfur are among the most abundant. Generally, but not invariably, the elements of lower atomic weight are more abundant than those of higher atomic weight.
Take a careful look at the list of elements in the preceding paragraph. Two of the most abundant are hydrogen and oxygen (which make up water); add carbon and nitrogen and you are starting to write the prescription for the chemistry of an astronomy student. We are made of elements that are common in the universe—just mixed together in a far more sophisticated form (and a much cooler environment) than in a star.
As we mentioned in The Spectra of Stars (and Brown Dwarfs) section, astronomers use the term “metals” to refer to all elements heavier than hydrogen and helium. The fraction of a star’s mass that is composed of these elements is referred to as the star’s metallicity. The metallicity of the Sun, for example, is 0.02, since 2% of the Sun’s mass is made of elements heavier than helium.
Appendix K lists how common each element is in the universe (compared to hydrogen); these estimates are based primarily on investigation of the Sun, which is a typical star. Some very rare elements, however, have not been detected in the Sun. Estimates of the amounts of these elements in the universe are based on laboratory measurements of their abundance in primitive meteorites, which are considered representative of unaltered material condensed from the solar nebula (see the Cosmic Samples and the Origin of the Solar System chapter).
Radial Velocity
When we measure the spectrum of a star, we determine the wavelength of each of its lines. If the star is not moving with respect to the Sun, then the wavelength corresponding to each element will be the same as those we measure in a laboratory here on Earth. But if stars are moving toward or away from us, we must consider the Doppler effect. We should see all the spectral lines of moving stars shifted toward the red end of the spectrum if the star is moving away from us, or toward the blue (violet) end if it is moving toward us (Figure \(\PageIndex{2}\)). The greater the shift, the faster the star is moving. Such motion, along the line of sight between the star and the observer, is called radial velocity and is usually measured in kilometers per second.
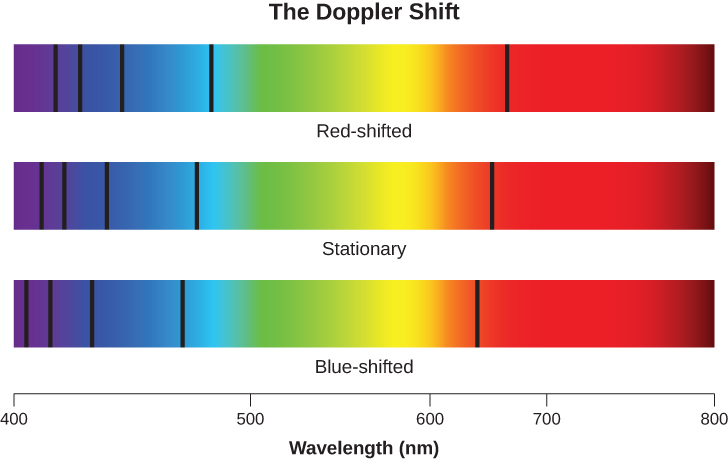
William Huggins, pioneering yet again, in 1868 made the first radial velocity determination of a star. He observed the Doppler shift in one of the hydrogen lines in the spectrum of Sirius and found that this star is moving toward the solar system. Today, radial velocity can be measured for any star bright enough for its spectrum to be observed. As we will see in The Stars: A Celestial Census, radial velocity measurements of double stars are crucial in deriving stellar masses.
Proper Motion
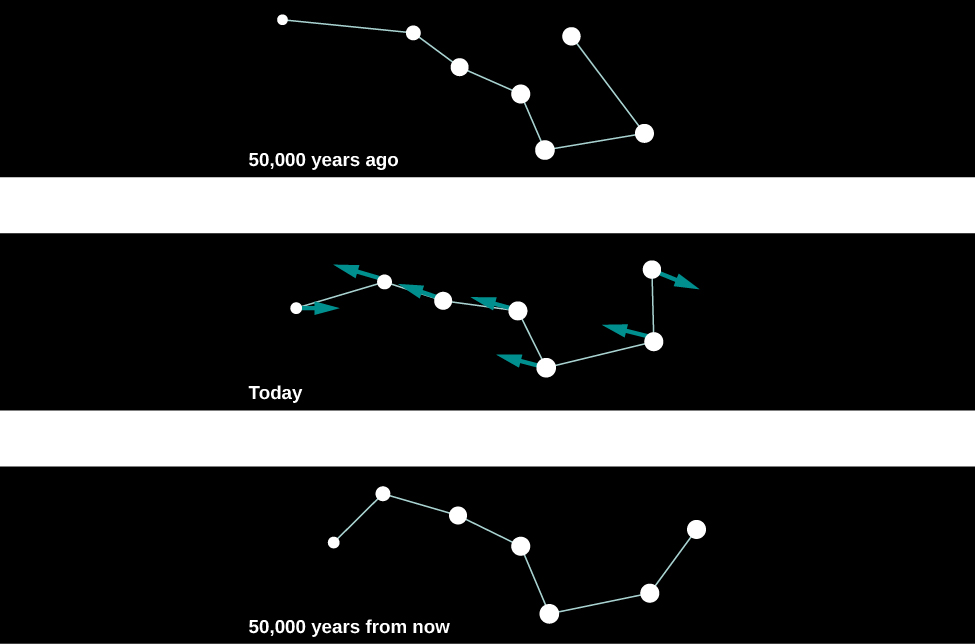
There is another type of motion stars can have that cannot be detected with stellar spectra. Unlike radial motion, which is along our line of sight (i.e., toward or away from Earth), this motion, called proper motion, is transverse: that is, across our line of sight. We see it as a change in the relative positions of the stars on the celestial sphere (Figure \(\PageIndex{3}\)). These changes are very slow. Even the star with the largest proper motion takes 200 years to change its position in the sky by an amount equal to the width of the full Moon, and the motions of other stars are smaller yet.

For this reason, with our naked eyes, we do not notice any change in the positions of the bright stars during the course of a human lifetime. If we could live long enough, however, the changes would become obvious. For example, some 50,000 years from now, terrestrial observers will find the handle of the Big Dipper unmistakably more bent than it is now (Figure \(\PageIndex{4}\)).
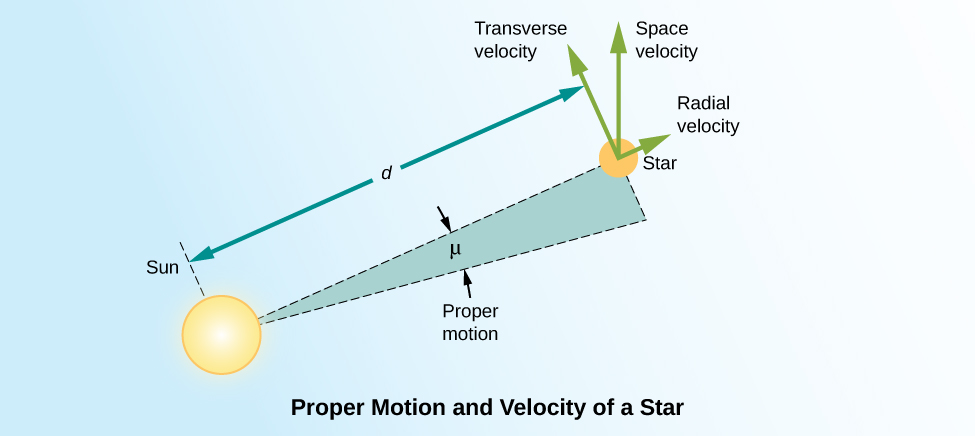
We measure the proper motion of a star in arcseconds (1/3600 of a degree) per year. That is, the measurement of proper motion tells us only by how much of an angle a star has changed its position on the celestial sphere. If two stars at different distances are moving at the same velocity perpendicular to our line of sight, the closer one will show a larger shift in its position on the celestial sphere in a year’s time. As an analogy, imagine you are standing at the side of a freeway. Cars will appear to whiz past you. If you then watch the traffic from a vantage point half a mile away, the cars will move much more slowly across your field of vision. In order to convert this angular motion to a velocity, we need to know how far away the star is.
To know the true space velocity of a star—that is, its total speed and the direction in which it is moving through space relative to the Sun—we must know its radial velocity, proper motion, and distance (Figure \(\PageIndex{5}\)). A star’s space velocity can also, over time, cause its distance from the Sun to change significantly. Over several hundred thousand years, these changes can be large enough to affect the apparent brightnesses of nearby stars. Today, Sirius, in the constellation Canis Major (the Big Dog) is the brightest star in the sky, but 100,000 years ago, the star Canopus in the constellation Carina (the Keel) was the brightest one. A little over 200,000 years from now, Sirius will have moved away and faded somewhat, and Vega, the bright blue star in Lyra, will take over its place of honor as the brightest star in Earth’s skies.
Rotation
We can also use the Doppler effect to measure how fast a star rotates. If an object is rotating, then one of its sides is approaching us while the other is receding (unless its axis of rotation happens to be pointed exactly toward us). This is clearly the case for the Sun or a planet; we can observe the light from either the approaching or receding edge of these nearby objects and directly measure the Doppler shifts that arise from the rotation.
Stars, however, are so far away that they all appear as unresolved points. The best we can do is to analyze the light from the entire star at once. Due to the Doppler effect, the lines in the light that come from the side of the star rotating toward us are shifted to shorter wavelengths and the lines in the light from the opposite edge of the star are shifted to longer wavelengths. You can think of each spectral line that we observe as the sum or composite of spectral lines originating from different speeds with respect to us. Each point on the star has its own Doppler shift, so the absorption line we see from the whole star is actually much wider than it would be if the star were not rotating. If a star is rotating rapidly, there will be a greater spread of Doppler shifts and all its spectral lines should be quite broad. In fact, astronomers call this effect line broadening, and the amount of broadening can tell us the speed at which the star rotates (Figure \(\PageIndex{6}\)).
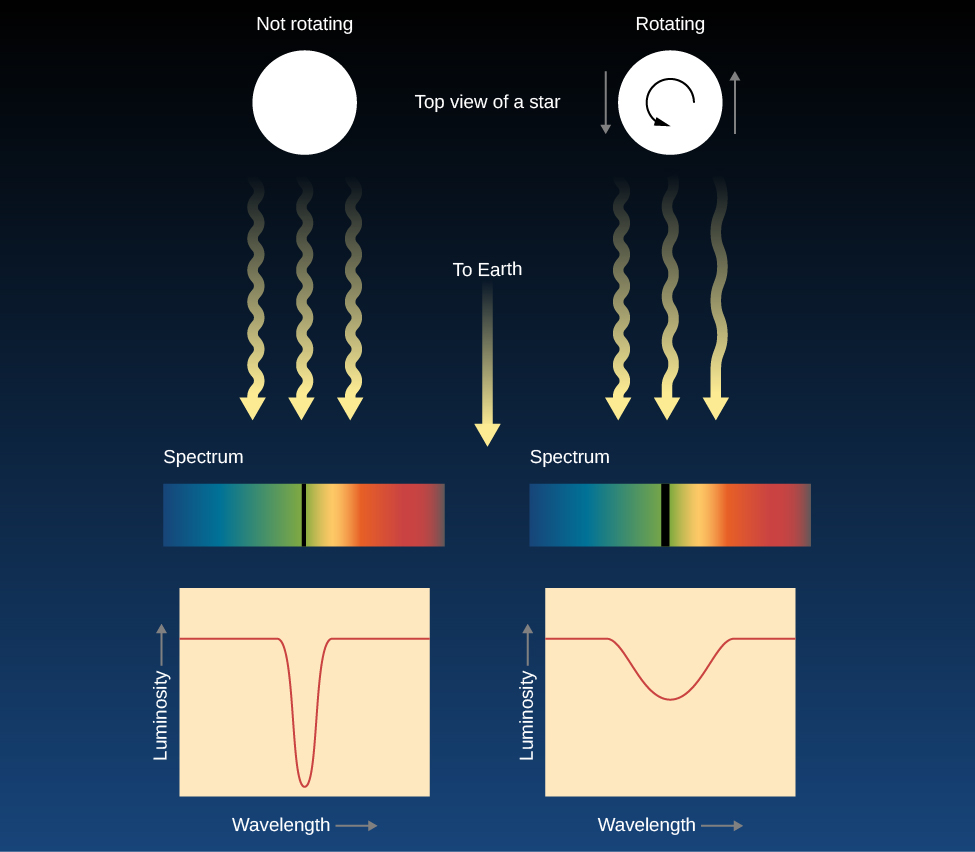
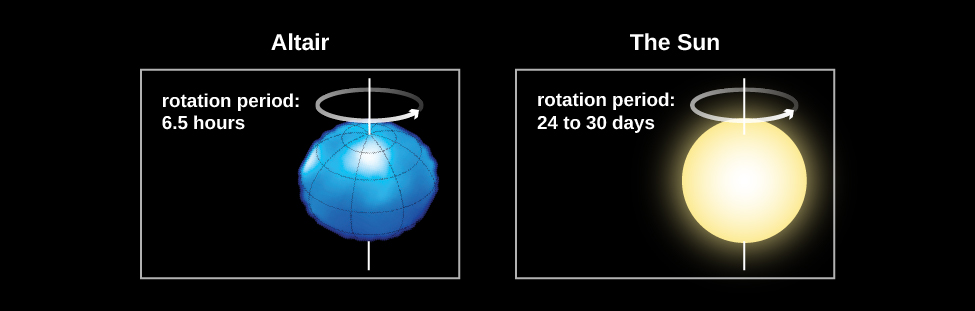
Measurements of the widths of spectral lines show that many stars rotate faster than the Sun, some with periods of less than a day! These rapid rotators spin so fast that their shapes are “flattened” into what we call oblate spheroids. An example of this is the star Vega, which rotates once every 12.5 hours. Vega’s rotation flattens its shape so much that its diameter at the equator is 23% wider than its diameter at the poles (Figure \(\PageIndex{7}\)). The Sun, with its rotation period of about a month, rotates rather slowly. Studies have shown that stars decrease their rotational speed as they age. Young stars rotate very quickly, with rotational periods of days or less. Very old stars can have rotation periods of several months.
As you can see, spectroscopy is an extremely powerful technique that helps us learn all kinds of information about stars that we simply could not gather any other way. We will see in later chapters that these same techniques can also teach us about galaxies, which are the most distant objects that can we observe. Without spectroscopy, we would know next to nothing about the universe beyond the solar system.
ASTRONOMY AND PHILANTHROPY
Throughout the history of astronomy, contributions from wealthy patrons of the science have made an enormous difference in building new instruments and carrying out long-term research projects. Edward Pickering’s stellar classification project, which was to stretch over several decades, was made possible by major donations from Anna Draper. She was the widow of Henry Draper, a physician who was one of the most accomplished amateur astronomers of the nineteenth century and the first person to successfully photograph the spectrum of a star. Anna Draper gave several hundred thousand dollars to Harvard Observatory. As a result, the great spectroscopic survey is still known as the Henry Draper Memorial, and many stars are still referred to by their “HD” numbers in that catalog (such as HD 209458).
In the 1870s, the eccentric piano builder and real estate magnate James Lick (Figure \(\PageIndex{8}\)) decided to leave some of his fortune to build the world’s largest telescope. When, in 1887, the pier to house the telescope was finished, Lick’s body was entombed in it. Atop the foundation rose a 36-inch refractor, which for many years was the main instrument at the Lick Observatory near San Jose.

The Lick telescope remained the largest in the world until 1897, when George Ellery Hale persuaded railroad millionaire Charles Yerkes to finance the construction of a 40-inch telescope near Chicago. More recently, Howard Keck, whose family made its fortune in the oil industry, gave $70 million from his family foundation to the California Institute of Technology to help build the world’s largest telescope atop the 14,000-foot peak of Mauna Kea in Hawaii (see the chapter on Astronomical Instruments to learn more about these telescopes). The Keck Foundation was so pleased with what is now called the Keck telescope that they gave $74 million more to build Keck II, another 10-meter reflector on the same volcanic peak.
Now, if any of you become millionaires or billionaires, and astronomy has sparked your interest, do keep an astronomical instrument or project in mind as you plan your estate. But frankly, private philanthropy could not possibly support the full enterprise of scientific research in astronomy. Much of our exploration of the universe is financed by federal agencies such as the National Science Foundation and NASA in the United States, and by similar government agencies in the other countries. In this way, all of us, through a very small share of our tax dollars, are philanthropists for astronomy.
Summary
Spectra of stars of the same temperature but different atmospheric pressures have subtle differences, so spectra can be used to determine whether a star has a large radius and low atmospheric pressure (a giant star) or a small radius and high atmospheric pressure. Stellar spectra can also be used to determine the chemical composition of stars; hydrogen and helium make up most of the mass of all stars. Measurements of line shifts produced by the Doppler effect indicate the radial velocity of a star. Broadening of spectral lines by the Doppler effect is a measure of rotational velocity. A star can also show proper motion, due to the component of a star’s space velocity across the line of sight.
Glossary
- giant
- a star of exaggerated size with a large, extended photosphere
- proper motion
- the angular change per year in the direction of a star as seen from the Sun
- radial velocity
- motion toward or away from the observer; the component of relative velocity that lies in the line of sight
- space velocity
- the total (three-dimensional) speed and direction with which an object is moving through space relative to the Sun


