5.5: The Equation of Transfer
The equation of transfer deals with the transfer of radiation through an atmosphere that is simultaneously absorbing, scattering and emitting.
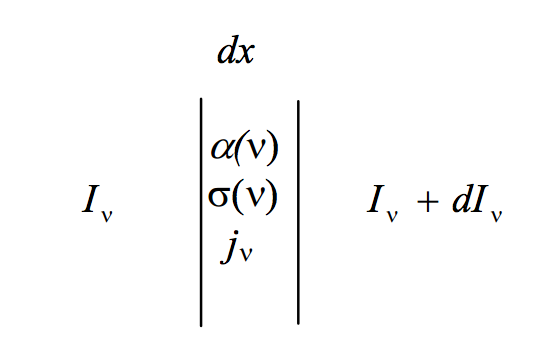
\(\text{FIGURE V.1}\)
Suppose that, between \(x\) and \(x + dx\) the absorption coefficient and the scattering coefficient at frequency \(\nu\) are \(\alpha (\nu)\) and \(\sigma (\nu)\), and the emission coefficient per unit frequency interval is \(j_{\nu} d\nu\). In this interval, suppose that the specific intensity per unit frequency interval increases from \(I_{\nu}\) to \(I_{\nu} + dI_{\nu}\) (\(dI_{\nu}\) might be positive or negative). The specific intensity will be reduced by absorption and scattering and increased by emission. Thus:
\[dI_{\nu} = - [I_{\nu} \alpha (\nu) + I_{\nu} \sigma (\nu) - j_{\nu} (\nu) ] dx. \label{5.5.1} \tag{5.5.1}\]
This is one form - the most basic form - of the equation of transfer. Notice that \(\alpha\) and \(\sigma\) do not have a subscript.