7.25: Some forbidden lines worth knowing
- Page ID
- 8948
The states in the ground level of an atom are the only stable states. Atoms may be raised to higher levels by collisions, but these excited states are not very stable, and an atom in an excited state will very soon de-excite by radiative emission of a photon. Lifetimes in the excited states are typically of the order of nanoseconds. However, the probability of de-excitation by emission of magnetic dipole or electric quadrupole radiation is much smaller than that for electric dipole radiation, and the lifetimes of excited states for \(\text{M}1\) or \(\text{E}2\) radiation may be seconds or even minutes. Such states are called metastable states. In normal laboratory conditions the interval between interatomic collisions (or collisions with the wall of the containing vessel) is very much shorter than the mean lifetime of a metastable level. (You can work out the inter-collision time from kinetic theory of gases.) Thus an atom will be knocked out of a metastable level by collision long before it has had a chance to emit \(\text{M}1\) or \(\text{E}2\) radiation. This is not so in very thin gases in some astronomical sources, such as the aurora or in emission nebulae. In such milieus collisions are few and far between, giving ample time for \(\text{M}1\) or \(\text{E}2\) radiative de-excitation.
It is worth noting, however, that the condition for the successful emission of \(\text{M}1\) or \(\text{E}2\) radiation is not quite as simple as supposing that the mean lifetime of a metastable level must be less than the intercollision interval. A collision may be inelastic, in which case some of the kinetic energy is absorbed and the metastable atom makes an upward transition; or it may be superelastic, in which case the metastable atoms undergoes a radiationless downward transition, the excess energy going to increase the kinetic energy of the colliding particle; or the collision may be elastic, in which case there is no change in kinetic energy and the metastable atom remains in its metastable state. In order to determine the condition for emission or non-emission of "forbidden" radiation, it is necessary to take account of the probability of these several processes. In practice the probability that a collision will be inelastic or superelastic may be quite small, so that very few collisions result in removing an atom from its metastable state. Thus it is quite possible for \(\text{M}1\) or \(\text{E}2\) lines to be observed even if the mean time between collisions is appreciably less than the mean lifetime of a metastable state − though under laboratory conditions, the collision frequency is altogether far too high. In astronomical sources where "forbidden" lines can be emitted, they are still very weak − but we have the advantage of being able to look through sources of vast extent.
Now that we understand how forbidden lines can be observed in astronomical sources, I give some examples of a few forbidden lines worth knowing.
The first three terms of \(\text{O}_\text{ I}\) are indicated schematically in figure VIII.4. They arise from the same \(p^4\) configuration, so the \(^3\text{P}\) term is an inverted term and none of the transitions are \(\text{E}1\). The transitions I have drawn are all "forbidden". I have drawn \(\text{E}2\) transitions as continuous lines and \(\text{M}1\) transitions as dashed lines. You should verify this by reference to the selection rules.
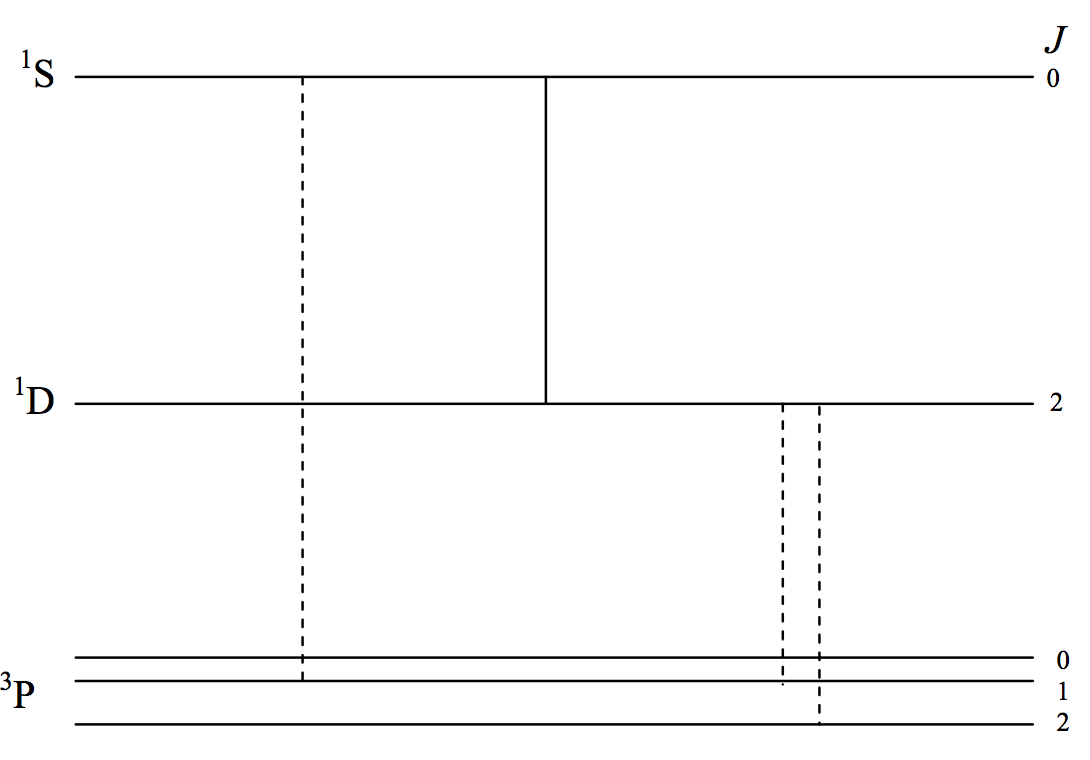
\(\text{FIGURE VII.4}\)
Starting from the left, the first two lines are at \(297.2\) and \(557.7 \ \text{nm}\). The mean lifetime of the \(^1 \text{S}_0\) level is of order about a second. The branching ratio is such that the ultraviolet \(\text{M}1\) (dashed) transition is very much less likely than the green \(\text{E}2\) transition at \(557.5 \ \text{nm}\). This green transition is usually the strongest auroral line, and you can even see that it is greenish in colour. The next time you look at an aurora you can reflect that electric quadrupole radiation is entering your eye! What a thrill! The \(557.7 \ \text{nm}\) line also occurs in the short-lived trains left by meteors. The two dashed (magnetic dipole) lines at the right are at \(636.3\) and \(630.0 \ \text{nm}\), and are red. The mean lifetime of the \(^1 \text{D}_2\) level is more than a minute, and they also appear in the auroral spectrum, but much higher in the atmosphere, where the inter-collision time is longer. When you look at an aurora you can usually see a red glow higher than the green glow. You are seeing magnetic dipole as well as electric quadrupole radiation!
There are several somewhat similar magnetic dipole and electric quadrupole lines involving the first three terms of the spectra of \([\text{O}_\text{ II}]\), \([\text{O}_\text{ III}]\), \([\text{N}_\text{ I}]\), \([\text{N}_\text{ II}]\), \([\text{N}_\text{ III}]\), which occur in the spectra of emission nebulae, including planetary nebulae. In figure VII.5 I illustrate just three lines of \([\text{O}_\text{ III}]\). The configuration of all terms is \(p^2\) and so the \(^3 \text{P}\) term is not inverted. The transitions \(^3\text{P}_2 - \ ^1\text{D}_2\) and \(^3\text{P}_2 - \ ^1 \text{D}_2\) (notice - no parity change) are at \(500.7\) and \(495.9 \ \text{nm}\) and are among the strongest observed in nebulae, and are often denoted by \(\text{N}_1\) and \(\text{N}_2\), although they have nothing whatever to do with nitrogen, the letter \(\text{N}\) presumably signifying "nebular". I would strongly discourage such notation. The transition \(^1\text{D}_2 - \ ^1\text{S}_0\) is at \(436.3 \ \text{nm}\). Before these lines were understood, they were referred to as "nebulium".
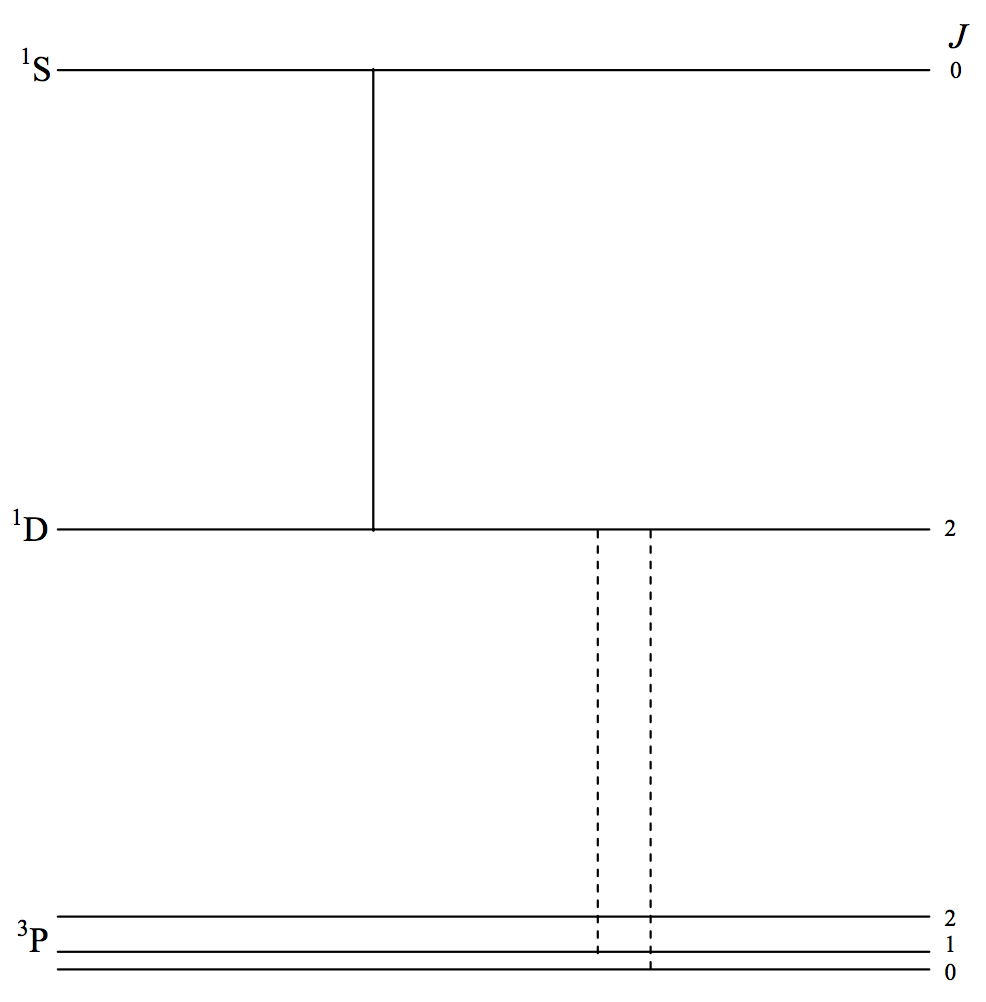
\(\text{FIGURE VII.5}\)
Before the spectrum of the solar corona was understood, the emission lines from the corona were ascribed to "coronium", but it is now known that they are "forbidden" lines from highly-ionized metals. The separation between levels within a single term is very large for highly-ionized atoms, and many of the observed lines in the coronal spectrum are magnetic dipole lines connecting two levels within the same term. For example, one of the strongest of the coronal lines, the green line at \(530.3 \ \text{nm}\), arises from the ion \(\text{Fe}^{13+}\) − that is to say the spectrum \([\text{Fe}_\text{ XIV}]\). This is isoelectronic with the neutral aluminium atom, and the ground term of the \(KL3s^2(^1\text{S})3p\) configuration is a normal \(^2 \text{P}^\text{o}\) term with two levels − \(J = \frac{1}{2}\) and \(\frac{3}{2}\). In \(\text{Al}_\text{ I}\) the separation in term value of these levels is only \(112 \ \text{cm}^{-1}\), but they are much more widely spaced in \(\text{Fe}_\text{ XIV}\) so that, in this spectrum, the wavelength of \(^2 \text{P}_{\frac{1}{2}}^\text{o} - \ ^2 \text{P}_\frac{3}{2}^\text{o}\) is \(530.3 \ \text{nm}\).
The last example is the famous \(21\)-\(\text{cm}\) transition of neutral hydrogen, \(\text{H}_\text{ I}\). Here, the lowest level is \(^2\text{S}_\frac{1}{2}\), which is the one and only level is the ground term, \(^2 \text{S}\). The level is split into two hyperfine levels as a result of the interaction between the total electronic angular momentum \((J=\frac{1}{2})\) and the nuclear spin \((I=\frac{1}{2}\)), the \(F\)-values of the two hyperfine levels being \(0\) and \(1\). The \(21\)-\(\text{cm}\) line is a magnetic dipole transition between these two hyperfine levels. The nuclear spin of deuterium is \(I = 1\), and consequently the ground level of deuterium is split into hyperfine levels with \(F = \frac{1}{2}\) and \(\frac{3}{2}\). A transition between these two is predicted at \(92 \ \text{cm}\), but apparently there is as yet no unambiguous detection of it from an astronomical source.


