1.1: Time Dilation

Einstein developed much of his understanding of relativity through the use of gedanken, or thought, experiments. In a gedanken experiment, Einstein would imagine an experiment that could not be performed due to technological limitations, and “perform” the experiment in his head. By analyzing the results of these experiments, he was lead to a deeper understanding of his theory.

In developing his understanding of the relativity of time, Einstein imagined what he considered the simplest possible clock, consisting of a mirror on the floor and a mirror on the ceiling of a train car, and a light pulse bouncing back and forth between the mirrors. Each reflection of the light pulse serves as a “tick” of the clock.

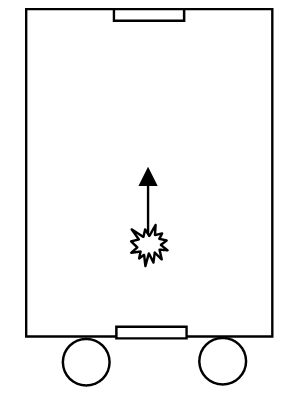
Figure $\PageIndex{1}$: Einstein's simple "clock".

Now imagine two observers and the train car traveling to the right at speed $v$. A passenger on the train will see the light pulse travel a vertical path from floor to ceiling. An observer at rest on the earth, however, will see the train displaced to the right during the time it takes the pulse to travel from floor to ceiling, and hence see the light pulse follow an angled path.

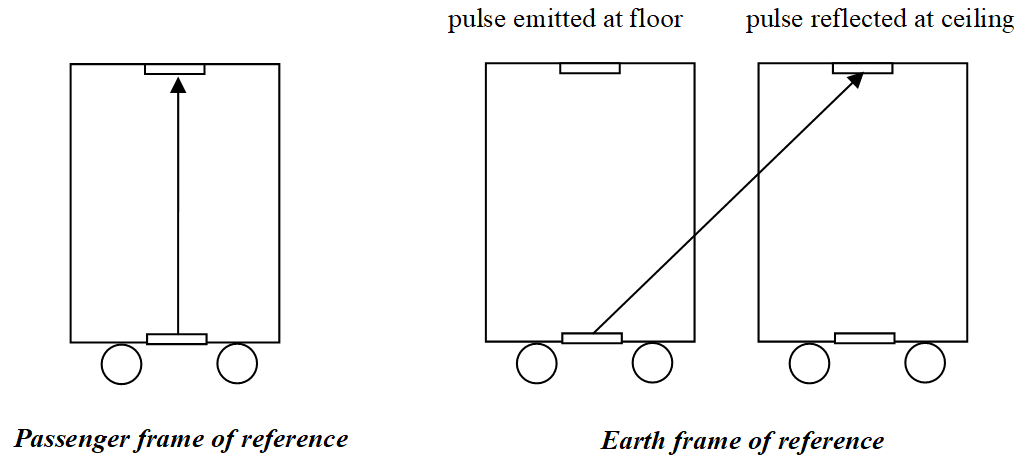
Figure $\PageIndex{2}$: Einstein's simple "clock" in motion.

Let $\Delta t$ represent the travel time from floor to ceiling measured on the earth, and $\Delta t_o$ represent the travel time from floor to ceiling measured on the train. Based on these definitions, and the speed of the train ($v$), the distances in the diagram can be determined.

You do remember from your study of electromagnetism that the speed of electromagnetic waves is the same in all frames of reference, don’t you?

By Pythagoras’ Theorem,

$$(c\Delta T)^2 = (v\Delta t)^2 + (c\Delta t_o)^2$$

$$(c\Delta T)^2 - (v\Delta t)^2 = (c\Delta t_o)^2$$

$$(c^2 -v^2) \Delta t^2 = c^2 \Delta t_o^2$$

$$\left( 1 - \dfrac{v^2}{c^2} \right) \Delta t^2 = \Delta t_o^2$$

$$\Delta t = \dfrac{\Delta _o}{\sqrt{1 - \dfrac{v^2}{c^2} }} \label{TD1}$$

Therefore, since the denominator is less than 1 for any speed $v<c$, the time interval between the “ticks” of the clock measured on the earth is greater than the time interval measured on the train. To earth-bound observers, the clock is ticking slower than normal. Einstein proposed that this is not a property of the clock, but rather a reflection of the fact that time itself passes slower for an object is in motion.

Using Time Dilation

The half-life of a muon at rest is $2.2 \,\mu s$. One can store muons for a much longer time (as measured in the laboratory) by accelerating them to a speed very close to that of light and then keeping them circulating at that speed in an evacuated ring. Assume that you want to design a ring that can keep muons moving so fast that they have a laboratory half-life of $20 \mu s$. How fast will the muons have to be moving?

The time between two events, for example the “birth” and “death” of a muon, depends on who makes the measurements. Within any particular reference system, the familiar results of classical physics are valid. However, in comparing results between observers in different reference systems, a method of relating one observer’s measurements to another is needed.

Equation $\ref{TD1}$ for time dilation is typically written in the form

$$\Delta t =\gamma (\Delta t_o) \label{TD2}$$

where

• $\Delta t_o$ is the proper time, the time between two events in the frame of reference in which both events occur at the same spatial point,
• $\Delta t$ is the time between the same two events in a different frame, moving at relative speed $v$,
• and $\gamma$ is the Lorentz factor, given by

$$\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2} }} \label{LF}$$

In the muon’s frame of reference, the muon’s are at rest and hence have a half-life of $2.2 \,\mu s$. Moreover, this is a proper time since in this frame of reference both the birth and death of the muons occur at the same point. (Since the muons are not moving, everything that happens to them happens at the same point.)

$$\Delta t = \gamma (\Delta t_o)$$

$$20 \, \mu s = \gamma (2.2 \,\mu s)$$

$$\begin{align} \gamma &= \dfrac{ 20\, \mu s}{2.2\, \mu s} \\[5pt] &= 9.09 \end{align}$$

Using Equation $\ref{LF}$

$$9.09 = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2} }}$$

$$1 - \dfrac{v^2}{c^2} = \left( \dfrac{1}{9.09} \right)^2$$

$$\dfrac{v^2}{c^2} = 1 - \left( \dfrac{1}{9.09} \right)^2$$

$$\dfrac{v^2}{c^2} = 0.9879$$

$$v = 0.994c$$

To get this level of time dilation, the muons have be me moving at 99.4% the speed of light.

Time Dilation at Everyday Speeds

The cruising speed of a jet airplane is approximately 250 m/s relative to the earth. For each hour of earth-time that passes, how much less time passes for the passengers on the plane?

The time interval measured by the passengers is the proper time, $\Delta t_o$, so we start with Equation $\ref{TD1}$

$$\Delta t = \dfrac{\Delta t_o}{\sqrt{1 - \dfrac{v^2}{c^2} }} \nonumber$$

$$\Delta t_o = \Delta t \sqrt{1 - \dfrac{v^2}{c^2} }$$

$$\Delta t_o = ( 1\,hr) \sqrt{1 - \dfrac{250^2}{(3 \times 10^8)^2} }$$

$$\Delta t_o = ( 1\,hr) \sqrt{1 - 6.94 \times 10^{-13} } \label{eq10}$$

Unfortunately, at this point my calculator tells me that $\Delta t_o = 1 \,hr$, which is obviously not true. I need a better way to deal with the extremely small numbers that sometimes show up in relativity. One way to do this is with the binomial approximation.

Expressions of the form:

$$\left(1+x \right)^n$$

where $x$ is much less than 1 can be approximated by:

$$\left(1+x \right)^n \approx 1 + nx$$

if $x \ll 1$

Using this approximation allows Equation $\ref{eq10}$ to be simplified:

$$\Delta t_o = ( 1\,hr) \sqrt{1 - 6.94 \times 10^{-13} } \label{eq11}$$

$$\Delta t_o = ( 1\,hr) \left(1 - 6.94 \times 10^{13} \right)^{1/2} \label{eq12}$$

$$\Delta t_o \approx ( 1\,hr) \left( 1 - \left(\dfrac{1}{2} \right) 6.94 \times 10^{-13} \right)$$

$$\Delta t_o \approx 1\,hr- 3.47 \times 10^{-13} hr$$

$$\Delta t_o \approx 1\,hr- 1.25 \times 10^{-9} s$$

Thus, for every hour that passes on earth, 1.25 nanoseconds less time passes on the airplane! This may seem like an incredibly small amount of time (and it is) but this effect has been measured in numerous experiments.