4.3: Pair Production
( \newcommand{\kernel}{\mathrm{null}\,}\)
In addition to the photoelectric effect (photon absorption) and Compton scattering (photon scattering), there is a third process by which photons can lose energy in their interaction with matter. In this process, termed pair production, a photon can simply vanish and in its place a matter-antimatter pair of particles can appear. This phenomenon is a wonderful illustration of the fact that mass is not conserved, since the mass of the electron and positron can be created from the energy of the massless photon. Of course, the photon must have sufficient energy to create the rest masses of the two new particles.
Typically, this process occurs in the vicinity of a nucleus and an electron-positron pair is formed. The effect is sketched below:
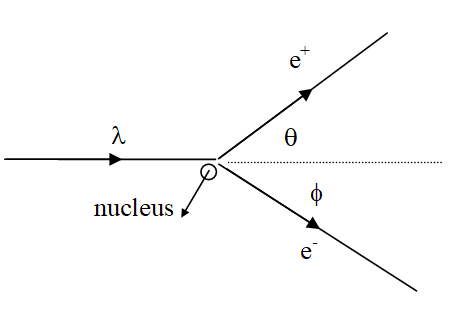
First, let’s try to imagine a simpler version of this phenomenon, with no nucleus present and the electron and positron both traveling in the same direction as the initial photon. Energy conservation would lead to:
E_{photon} = E_{electron} + E_{positron}
and x-momentum conservation:
pc_{photon} = pc_{electron} + pc_{positron}
Using
E_{total}^2 = (pc)^2 + (mc^2)^2
energy conservation can be written as:
\sqrt{pc_{photon}^2+(0)^2} = \sqrt{pc_{electron}^2+0.511^2}+\sqrt{pc_{photon}^2 +0.511^2}
pc_{photon} = \sqrt{pc_{electron}^2+0.511^2}+\sqrt{pc_{photon}^2 +0.511^2}
Setting this equation equal to the momentum conservation equation leads to:
\sqrt{ pc_{electron}^2 + 0.511^2} + \sqrt{pc_{positron}^2 +0.511^2} = pc_{electron} + pc_{electron}
Hopefully it’s clear that this equation is garbage! The left-side of the equation is larger than the right-side of the equation for any real values of momentum. This means that the “simplified” version of pair production discussed above is impossible. The only way pair production can occur is if a third body (the nucleus) is present to participate in the sharing of energy and momentum.
However, if we try to set-up and solve the conservation laws for the real pair production process we will get bogged down in a rather large amount of algebra. Instead, let’s make an approximation that since the nucleus is much, much more massive than the electron and positron it can “absorb” the proper amount of momentum to guarantee momentum conservation without “absorbing” very much of the kinetic energy. In a sense, we will ignore the nucleus during the solution of the problem, and then once we have a solution we will check to see if ignoring the nucleus was a reasonable choice.
As an example, consider the problem below.
Example \PageIndex{1}
A 3.0 MeV photon interacts with a lead nucleus and creates an electron-positron pair. The electron and positron travel perpendicular to the initial direction of travel of the photon.
- Find the kinetic energies of the electron and positron assuming the nucleus is at rest after the collision.
- Find the kinetic energy of the lead nucleus needed to ensure momentum conservation. Would this amount of kinetic energy greatly affect the result in part a?
Solution
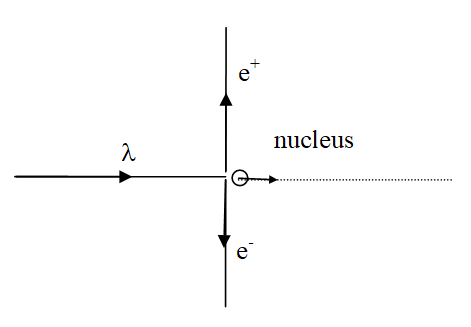
Energy conservation (ignoring the energy of the nucleus) leads to:
E_{photon} = E_{electron}+E_{positron}
3 = E_{electron}+E_{positron}
and y-momentum conservation (ignoring the nucleus again):
0 = -pc_{electron} + pc_{positron}
pc_{electron} = pc_{positron}
Since the pair have equal momenta, they must have equal energy, so:
3 =2E_{either}
E_{either} - 1.5 \text{ MeV}
KE_{either} = (1.5-0.511)\text{ MeV}
KE_{either} 0.989\text{ MeV}
To ensure that x-momentum is conserved,
pc_{photon} = pc_{nucleus}
3\text{ MeV} = pc_{nucleus}
Using E_{total}^2 =(pc)^2 +(mc^2)^2 and noting that the atomic mass of a lead atom is 207.2 \text{ u} = 193007 \text{ MeV} yields,
E_{nucleus}=\sqrt{3^2+193007^2}
E_{nucleus}=193007\text{ MeV} \sqrt{1+\frac{9}{193007^2}}
then simplify using the binomial expansion,
E_{nucleus}=193007\text{ MeV} \bigg(1+\frac{1}{2}\frac{9}{193007^2}\bigg)
E_{nucleus}=193007\text{ MeV} (1+1.2\times10^{-10})
E_{nucleus}=193007\text{ MeV} + 2.33\times10^{-5} \text{ MeV}
KE_{nucleus} = 2.33 \times 10^{-5} \text{ MeV}
KE_{nucleus} =23.3\text{ eV}
Thus, the nucleus can preserve momentum conservation while only “stealing” a ridiculously small portion of the total energy available. Thus, we can ignore the presence of the nucleus while dividing up the energy of the incoming photon between the electron and positron.


