11.E: Fields (Exercises)
- Page ID
- 1012
1. The gap between the electrodes in an automobile engine's spark plug is 0.060 cm. To produce an electric spark in a gasoline-air mixture, an electric field of \(3.0\times10^6\) V/m must be achieved. On starting a car, what minimum voltage must be supplied by the ignition circuit? Assume the field is uniform.(answer check available at lightandmatter.com)
(b) The small size of the gap between the electrodes is inconvenient because it can get blocked easily, and special tools are needed to measure it. Why don't they design spark plugs with a wider gap?
2. (a) As suggested in example 9 on page 573, use approximations to show that the expression given for the electric field approaches \(kQ/d^2\) for large \(d\).
(b) Do the same for the result of example 12 on page 577.
3. Astronomers believe that the mass distribution (mass per unit volume) of some galaxies may be approximated, in spherical coordinates, by \(\rho=ae^{-br}\), for \(0\le r\le\infty\), where \(\rho\) is the density. Find the total mass.
4. (a) At time \(t=0\), a positively charged particle is placed, at rest, in a vacuum, in which there is a uniform electric field of magnitude \(E\). Write an equation giving the particle's speed, \(v\), in terms of \(t\), \(E\), and its mass and charge \(m\) and \(q\).(answer check available at lightandmatter.com)
(b) If this is done with two different objects and they are observed to have the same motion, what can you conclude about their masses and charges? (For instance, when radioactivity was discovered, it was found that one form of it had the same motion as an electron in this type of experiment.)
5. Show that the alternative definition of the magnitude of the electric field, \(|E|=\tau/D_t\sin\theta\), has units that make sense.
6. Redo the calculation of example 5 on page 566 using a different origin for the coordinate system, and show that you get the same result.
7. The definition of the dipole moment, \(\mathbf{D}=\sum q_i \mathbf{r}_i\), involves the vector \(\mathbf{r}_i\) stretching from the origin of our coordinate system out to the charge \(q_i\). There are clearly cases where this causes the dipole moment to be dependent on the choice of coordinate system. For instance, if there is only one charge, then we could make the dipole moment equal zero if we chose the origin to be right on top of the charge, or nonzero if we put the origin somewhere else.
(a) Make up a numerical example with two charges of equal magnitude and opposite sign. Compute the dipole moment using two different coordinate systems that are oriented the same way, but differ in the choice of origin. Comment on the result.
(b) Generalize the result of part a to any pair of charges with equal magnitude and opposite sign. This is supposed to be a proof for any arrangement of the two charges, so don't assume any numbers.
(c) Generalize further, to \(n\) charges.
9. Find an arrangement of charges that has zero total charge and zero dipole moment, but that will make nonvanishing electric fields.
10. As suggested in example 11 on page 575, show that you can get the same result for the on-axis field by differentiating the voltage

b / Problem 11.
11. Three charges are arranged on a square as shown. All three charges are positive. What value of \(q_2/q_1\) will produce zero electric field at the center of the square?(answer check available at lightandmatter.com)
12. This is a one-dimensional problem, with everything confined to the \(x\) axis. Dipole A consists of a \(-1.000\) C charge at \(x=0.000\) m and a \(1.000\) C charge at \(x=1.000\) m. Dipole B has a \(-2.000\) C charge at \(x=0.000\) m and a \(2.000\) C charge at \(x=0.500\) m.
(a) Compare the two dipole moments.
(b) Calculate the field created by dipole A at \(x=10.000\) m, and compare with the field dipole B would make. Comment on the result.(answer check available at lightandmatter.com)
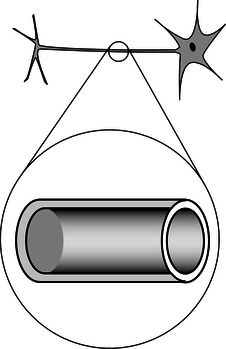
c / Problem 13.
13. In our by-now-familiar neuron, the voltage difference between the inner and outer surfaces of the cell membrane is about \(V_{out}-V_{in}=-70\ \text{mV}\) in the resting state, and the thickness of the membrane is about 6.0 nm (i.e., only about a hundred atoms thick). What is the electric field inside the membrane?(answer check available at lightandmatter.com)
14. A proton is in a region in which the electric field is given by \(E=a+bx^3\). If the proton starts at rest at \(x_1=0\), find its speed, \(v\), when it reaches position \(x_2\). Give your answer in terms of \(a\), \(b\), \(x_2\), and \(e\) and \(m\), the charge and mass of the proton.(answer check available at lightandmatter.com)
15. (a) Given that the on-axis field of a dipole at large distances is proportional to \(D/r^3\), show that its voltage varies as \(D/r^2\). (Ignore positive and negative signs and numerical constants of proportionality.)
(b) Write down an exact expression for the voltage of a two-charge dipole at an on-axis point, without assuming that the distance is large compared to the size of the dipole. Your expression will have to contain the actual charges and size of the dipole, not just its dipole moment. Now use approximations to show that, at large distances, this is consistent with your answer to part a.\hwhint{hwhint:dipolev}
16. A hydrogen atom is electrically neutral, so at large distances, we expect that it will create essentially zero electric field. This is not true, however, near the atom or inside it. Very close to the proton, for example, the field is very strong. To see this, think of the electron as a spherically symmetric cloud that surrounds the proton, getting thinner and thinner as we get farther away from the proton. (Quantum mechanics tells us that this is a more correct picture than trying to imagine the electron orbiting the proton.) Near the center of the atom, the electron cloud's field cancels out by symmetry, but the proton's field is strong, so the total field is very strong. The voltage in and around the hydrogen atom can be approximated using an expression of the form \(V=r^{-1}e^{-r}\). (The units come out wrong, because I've left out some constants.) Find the electric field corresponding to this voltage, and comment on its behavior at very large and very small \(r\). (solution in the pdf version of the book)
17. A carbon dioxide molecule is structured like O-C-O, with all three atoms along a line. The oxygen atoms grab a little bit of extra negative charge, leaving the carbon positive. The molecule's symmetry, however, means that it has no overall dipole moment, unlike a V-shaped water molecule, for instance. Whereas the voltage of a dipole of magnitude \(D\) is proportional to \(D/r^2\) (see problem 15), it turns out that the voltage of a carbon dioxide molecule at a distant point along the molecule's axis equals \(b/r^3\), where \(r\) is the distance from the molecule and \(b\) is a constant (cf. problem 9). What would be the electric field of a carbon dioxide molecule at a point on the molecule's axis, at a distance \(r\) from the molecule?(answer check available at lightandmatter.com)
18. A hydrogen atom in a particular state has the charge density (charge per unit volume) of the electron cloud given by \(\rho=ae^{-br}z^2\), where \(r\) is the distance from the proton, and \(z\) is the coordinate measured along the \(z\) axis. Given that the total charge of the electron cloud must be \(-e\), find \(a\) in terms of the other variables.
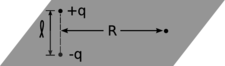
d / Problem 19.
19. A dipole has a midplane, i.e., the plane that cuts through the dipole's center, and is perpendicular to the dipole's axis. Consider a two-charge dipole made of point charges \(\pm q\) located at \(z=\pm\ell/2\). Use approximations to find the field at a distant point in the midplane, and show that its magnitude comes out to be \(kD/R^3\) (half what it would be at a point on the axis lying an equal distance from the dipole).
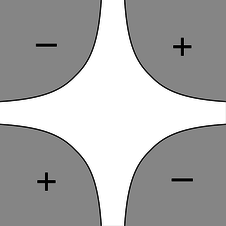
e / Problem 20.
20. The figure shows a vacuum chamber surrounded by four metal electrodes shaped like hyperbolas. (Yes, physicists do sometimes ask their university machine shops for things machined in mathematical shapes like this. They have to be made on computer-controlled mills.) We assume that the electrodes extend far into and out of the page along the unseen \(z\) axis, so that by symmetry, the electric fields are the same for all \(z\). The problem is therefore effectively two-dimensional. Two of the electrodes are at voltage \(+V_\text{o}\), and the other two at \(-V_\text{o}\), as shown. The equations of the hyperbolic surfaces are \(|xy|=b^2\), where \(b\) is a constant. (We can interpret \(b\) as giving the locations \(x=\pm b\), \(y=\pm b\) of the four points on the surfaces that are closest to the central axis.) There is no obvious, pedestrian way to determine the field or voltage in the central vacuum region, but there's a trick that works: with a little mathematical insight, we see that the voltage \(V=V_\text{o}b^{-2}xy\) is consistent with all the given information. (Mathematicians could prove that this solution was unique, but a physicist knows it on physical grounds: if there were two different solutions, there would be no physical way for the system to decide which one to do!) (a) Use the techniques of subsection 10.2.2 to find the field in the vacuum region, and (b) sketch the field as a “sea of arrows.”(answer check available at lightandmatter.com)
21. (a) A certain region of three-dimensional space has a voltage that varies as \(V=br^2\), where \(r\) is the distance from the origin. Use the techniques of subsection 10.2.2 to find the field.(answer check available at lightandmatter.com)
(b) Write down another voltage that gives exactly the same field.
22. (a) Example 10 on page 574 gives the field of a charged rod in its midplane. Starting from this result, take the limit as the length of the rod approaches infinity. Note that \(\lambda\) is not changing, so as \(L\) gets bigger, the total charge \(Q\) increases. \hwans{hwans:estrips}
(b) In the text, I have shown (by several different methods) that the field of an infinite, uniformly charged plane is \(2\pi k\sigma\). Now you're going to rederive the same result by a different method. Suppose that it is the \(x-y\) plane that is charged, and we want to find the field at the point \((0,0,z)\). (Since the plane is infinite, there is no loss of generality in assuming \(x=0\) and \(y=0\).) Imagine that we slice the plane into an infinite number of straight strips parallel to the \(y\) axis. Each strip has infinitesimal width \(dx\), and extends from \(x\) to \(x+dx\). The contribution any one of these strips to the field at our point has a magnitude which can be found from part a. By vector addition, prove the desired result for the field of the plane of charge.

f / Problem 23.
23. Consider the electric field created by a uniformly charged cylindrical surface that extends to infinity in one direction.
(a) Show that the field at the center of the cylinder's mouth is \(2\pi k\sigma\), which happens to be the same as the field of an infinite flat sheet of charge!
(b) This expression is independent of the radius of the cylinder. Explain why this should be so. For example, what would happen if you doubled the cylinder's radius?
24. In an electrical storm, the cloud and the ground act like a parallel-plate capacitor, which typically charges up due to frictional electricity in collisions of ice particles in the cold upper atmosphere. Lightning occurs when the magnitude of the electric field builds up to a critical value, \(E_c\), at which air is ionized.
(a) Treat the cloud as a flat square with sides of length \(L\). If it is at a height \(h\) above the ground, find the amount of energy released in the lightning strike.(answer check available at lightandmatter.com)
(b) Based on your answer from part a, which is more dangerous, a lightning strike from a high-altitude cloud or a low-altitude one?
(c) Make an order-of-magnitude estimate of the energy released by a typical lightning bolt, assuming reasonable values for its size and altitude. \(E_c\) is about \(10^6\) V/m.
25. (a) Show that the energy in the electric field of a point charge is infinite! Does the integral diverge at small distances, at large distances, or both? \hwhint{hwhint:epointinfty}
[4] (b) Now calculate the energy in the electric field of a uniformly charged sphere with radius \(b\). Based on the shell theorem, it can be shown that the field for \(r>b\) is the same as for a point charge, while the field for \(r\lt b\) is \(kqr/b^3\). (Example 38 shows this using a different technique.)
(answer check available at lightandmatter.com)

g / Problem 26.
26. The neuron in the figure has been drawn fairly short, but some neurons in your spinal cord have tails (axons) up to a meter long. The inner and outer surfaces of the membrane act as the “plates” of a capacitor. (The fact that it has been rolled up into a cylinder has very little effect.) In order to function, the neuron must create a voltage difference \(V\) between the inner and outer surfaces of the membrane. Let the membrane's thickness, radius, and length be \(t\), \(r\), and \(L\). (a) Calculate the energy that must be stored in the electric field for the neuron to do its job. (In real life, the membrane is made out of a substance called a dielectric, whose electrical properties increase the amount of energy that must be stored. For the sake of this analysis, ignore this fact.) \hwhint{hwhint:neuronenergy}(answer check available at lightandmatter.com)
(b) An organism's evolutionary fitness should be better if it needs less energy to operate its nervous system. Based on your answer to part a, what would you expect evolution to do to the dimensions \(t\) and \(r?\) What other constraints would keep these evolutionary trends from going too far?
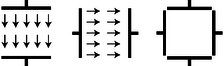
h / Problem 27.
27. The figure shows cross-sectional views of two cubical capacitors, and a cross-sectional view of the same two capacitors put together so that their interiors coincide. A capacitor with the plates close together has a nearly uniform electric field between the plates, and almost zero field outside; these capacitors don't have their plates very close together compared to the dimensions of the plates, but for the purposes of this problem, assume that they still have approximately the kind of idealized field pattern shown in the figure. Each capacitor has an interior volume of 1.00 \(\text{m}^3\), and is charged up to the point where its internal field is 1.00 V/m.
(a) Calculate the energy stored in the electric field of each capacitor when they are separate. (answer check available at lightandmatter.com)
(b) Calculate the magnitude of the interior field when the two capacitors are put together in the manner shown. Ignore effects arising from the redistribution of each capacitor's charge under the influence of the other capacitor.(answer check available at lightandmatter.com)
(c) Calculate the energy of the put-together configuration. Does assembling them like this release energy, consume energy, or neither?(answer check available at lightandmatter.com)
28. Find the capacitance of the surface of the earth, assuming there is an outer spherical “plate” at infinity. (In reality, this outer plate would just represent some distant part of the universe to which we carried away some of the earth's charge in order to charge up the earth.)(answer check available at lightandmatter.com)
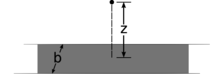
i / Problem 29.
29. (a) Show that the field found in example 10 on page 574 reduces to \(E=2k\lambda/R\) in the limit of \(L\rightarrow\infty\).
(b) An infinite strip of width \(b\) has a surface charge density \(\sigma\). Find the field at a point at a distance \(z\) from the strip, lying in the plane perpendicularly bisecting the strip. (answer check available at lightandmatter.com)
(c) Show that this expression has the correct behavior in the limit where \(z\) approaches zero, and also in the limit of \(z\gg b\). For the latter, you'll need the result of problem 22a, which is given on page 930.
30. A solid cylinder of radius \(b\) and length \(\ell\) is uniformly charged with a total charge \(Q\). Find the electric field at a point at the center of one of the flat ends.
31. Find the voltage at the edge of a uniformly charged disk. (Define \(V=0\) to be infinitely far from the disk.) (answer check available at lightandmatter.com)\hwhint{hwhint:vedgedisk}
32. Find the energy stored in a capacitor in terms of its capacitance and the voltage difference across it.(answer check available at lightandmatter.com)
33. (a) Find the capacitance of two identical capacitors in series.
(b) Based on this, how would you expect the capacitance of a parallel-plate capacitor to depend on the distance between the plates?
34. (a) Use complex number techniques to rewrite the function \(f(t)=4\sin\omega t+3\cos\omega t\) in the form \(A\sin(\omega t+\delta)\).(answer check available at lightandmatter.com)
(b) Verify the result using the trigonometric identity \(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\).
35. (a) Show that the equation \(V_L=LdI/dt\) has the right units.
(b) Verify that \(RC\) has units of time.
(c) Verify that \(L/R\) has units of time.
36. Find the inductance of two identical inductors in parallel.
37. Calculate the quantity \(i^i\) (i.e., find its real and imaginary parts).(answer check available at lightandmatter.com)
38. The wires themselves in a circuit can have resistance, inductance, and capacitance. Would “stray” inductance and capacitance be most important for low-frequency or for high-frequency circuits? For simplicity, assume that the wires act like they're in series with an inductor or capacitor.
39. Starting from the relation \(V=LdI/dt\) for the voltage difference across an inductor, show that an inductor has an impedance equal to \(L\omega\).
40. A rectangular box is uniformly charged with a charge density \(\rho\). The box is extremely long and skinny, and its cross-section is a square with sides of length \(b\). The length is so great in comparison to \(b\) that we can consider it as being infinite. Find the electric field at a point lying on the box's surface, at the midpoint between the two edges. Your answer will involve an integral that is most easily done using computer software.
41. A hollow cylindrical pipe has length \(\ell\) and radius \(b\). Its ends are open, but on the curved surface it has a charge density \(\sigma\). A charge \(q\) with mass \(m\) is released at the center of the pipe, in unstable equilibrium. Because the equilibrium is unstable, the particle acclerates off in one direction or the other, along the axis of the pipe, and comes shooting out like a bullet from the barrel of a gun. Find the velocity of the particle when it's infinitely far from the “gun.” Your answer will involve an integral that is difficult to do by hand; you may want to look it up in a table of integrals, do it online at integrals.com, or download and install the free Maxima symbolic math software from maxima.sourceforge.net.
42. If an FM radio tuner consisting of an LRC circuit contains a 1.0 \(\mu\text{H}\) inductor, what range of capacitances should the variable capacitor be able to provide?(answer check available at lightandmatter.com)
43. (a) Find the parallel impedance of a \(37\ \text{k}\Omega\) resistor and a 1.0 nF capacitor at \(f=1.0\times10^4\) Hz.(answer check available at lightandmatter.com)
(b) A voltage with an amplitude of 1.0 mV drives this impedance at this frequency. What is the amplitude of the current drawn from the voltage source, what is the current's phase angle with respect to the voltage, and does it lead the voltage, or lag behind it?(answer check available at lightandmatter.com)
44. A series LRC circuit consists of a 1.000 \(\Omega\) resistor, a 1.000 F capacitor, and a 1.000 H inductor. (These are not particularly easy values to find on the shelf at Radio Shack!)
(a) Plot its impedance as a point in the complex plane for each of the following frequencies: \(\omega\)=0.250, 0.500, 1.000, 2.000, and 4.000 Hz.
(b) What is the resonant angular frequency, \(\omega_{res}\), and how does this relate to your plot?(answer check available at lightandmatter.com)
(c) What is the resonant frequency \(f_{res}\) corresponding to your answer in part b?(answer check available at lightandmatter.com)
45. At a frequency \(\omega\), a certain series LR circuit has an impedance of \(1\ \Omega+(2\ \Omega)i\). Suppose that instead we want to achieve the same impedance using two circuit elements in parallel. What must the elements be?
46. (a) Use Gauss' law to find the fields inside and outside an infinite cylindrical surface with radius \(b\) and uniform surface charge density \(\sigma\).(answer check available at lightandmatter.com)
(b) Show that there is a discontinuity in the electric field equal to \(4\pi k \sigma\) between one side of the surface and the other, as there should be (see page 628).
(c) Reexpress your result in terms of the charge per unit length, and compare with the field of a line of charge.
(d) A coaxial cable has two conductors: a central conductor of radius \(a\), and an outer conductor of radius \(b\). These two conductors are separated by an insulator. Although such a cable is normally used for time-varying signals, assume throughout this problem that there is simply a DC voltage between the two conductors. The outer conductor is thin, as in part c. The inner conductor is solid, but, as is always the case with a conductor in electrostatics, the charge is concentrated on the surface. Thus, you can find all the fields in part b by superposing the fields due to each conductor, as found in part c. (Note that on a given length of the cable, the total charge of the inner and outer conductors is zero, so \(\lambda_1=-\lambda_2\), but \(\sigma_1\ne\sigma_2\), since the areas are unequal.) Find the capacitance per unit length of such a cable.(answer check available at lightandmatter.com)
47. In a certain region of space, the electric field is constant (i.e., the vector always has the same magnitude and direction). For simplicity, assume that the field points in the positive \(x\) direction. (a) Use Gauss's law to prove that there is no charge in this region of space. This is most easily done by considering a Gaussian surface consisting of a rectangular box, whose edges are parallel to the \(x\), \(y\), and \(z\) axes.
(b) If there are no charges in this region of space, what could be making this electric field?
48. (a) In a series LC circuit driven by a DC voltage (\(\omega=0\)), compare the energy stored in the inductor to the energy stored in the capacitor.
(b) Carry out the same comparison for an LC circuit that is oscillating freely (without any driving voltage).
(c) Now consider the general case of a series LC circuit driven by an oscillating voltage at an arbitrary frequency. Let \(\overline{U_L}\) and be the average energy stored in the inductor, and similarly for \(\overline{U_C}\). Define a quantity \(u=\overline{U_C}/(\overline{U_L}+\overline{U_C})\), which can be interpreted as the capacitor's average share of the energy, while \(1-u\) is the inductor's average share. Find \(u\) in terms of \(L\), \(C\), and \(\omega\), and sketch a graph of \(u\) and \(1-u\) versus \(\omega\). What happens at resonance? Make sure your result is consistent with your answer to part a.(answer check available at lightandmatter.com)
49. Use Gauss' law to find the field inside an infinite cylinder with radius \(b\) and uniform charge density \(\rho\). (The external field has the same form as the one in problem 46.)(answer check available at lightandmatter.com)
50. (a) In a certain region of space, the electric field is given by \(\mathbf{E}=bx\hat{\mathbf{x}}\), where \(b\) is a constant. Find the amount of charge contained within a cubical volume extending from \(x=0\) to \(x=a\), from \(y=0\) to \(y=a\), and from \(z=0\) to \(z=a\).
(b) Repeat for \(\mathbf{E}=bx\hat{\mathbf{z}}\).
(c) Repeat for \(\mathbf{E}=13bz\hat{\mathbf{z}}-7cz\hat{\mathbf{y}}\).
(d) Repeat for \(\mathbf{E}=bxz\hat{\mathbf{z}}\).
51. Light is a wave made of electric and magnetic fields, and the fields are perpendicular to the direction of the wave's motion, i.e., they're transverse. An example would be the electric field given by \(\mathbf{E}=b \hat{\mathbf{x}} \sin cz\), where \(b\) and \(c\) are constants. (There would also be an associated magnetic field.) We observe that light can travel through a vacuum, so we expect that this wave pattern is consistent with the nonexistence of any charge in the space it's currently occupying. Use Gauss's law to prove that this is true.
52. This is an alternative approach to problem 49, using a different technique. Suppose that a long cylinder contains a uniform charge density \(\rho\) throughout its interior volume.
(a) Use the methods of section 10.7 to find the electric field inside the cylinder. (answer check available at lightandmatter.com)
(b) Extend your solution to the outside region, using the same technique. Once you find the general form of the solution, adjust it so that the inside and outside fields match up at the surface.(answer check available at lightandmatter.com)
53. The purpose of this homework problem is to prove that the divergence is invariant with respect to translations. That is, it doesn't matter where you choose to put the origin of your coordinate system. Suppose we have a field of the form \(\mathbf{E}=ax\hat{\mathbf{x}}+by\hat{\mathbf{y}}+cz\hat{\mathbf{z}}\). This is the most general field we need to consider in any small region as far as the divergence is concerned. (The dependence on \(x\), \(y\), and \(z\) is linear, but any smooth function looks linear close up. We also don't need to put in terms like \(x\hat{\mathbf{y}}\), because they don't contribute to the divergence.) Define a new set of coordinates \((u,v,w)\) related to \((x,y,z)\) by
where \(p\), \(q\), and \(r\) are constants. Show that the field's divergence is the same in these new coordinates. Note that \(\hat{\mathbf{x}}\) and \(\hat{\mathbf{u}}\) are identical, and similarly for the other coordinates.
54. Using a techniques similar to that of problem 53, show that the divergence is rotationally invariant, in the special case of rotations about the \(z\) axis. In such a rotation, we rotate to a new \((u,v,z)\) coordinate system, whose axes are rotated by an angle \(\theta \) with respect to those of the \((x,y,z)\) system. The coordinates are related by
Find how the \(u\) and \(v\) components the field \(\mathbf{E}\) depend on \(u\) and \(v\), and show that its divergence is the same in this new coordinate system.
55. An electric field is given in cylindrical coordinates \((R,\phi,z)\) by \(E_R=ce^{-u|z|}R^{-1}\cos^2\phi\), where the notation \(E_R\) indicates the component of the field pointing directly away from the axis, and the components in the other directions are zero. (This isn't a completely impossible expression for the field near a radio transmitting antenna.) (a) Find the total charge enclosed within the infinitely long cylinder extending from the axis out to \(R=b\). (b) Interpret the \(R\)-dependence of your answer to part a.
56. Use Euler's theorem to derive the addition theorems that express \(\sin(a+b)\) and \(\cos(a+b)\) in terms of the sines and cosines of \(a\) and \(b\). (solution in the pdf version of the book)
57. Find every complex number \(z\) such that \(z^3=1\). (solution in the pdf version of the book)
58. Factor the expression \(x^3-y^3\) into factors of the lowest possible order, using complex coefficients. (Hint: use the result of problem 57.) Then do the same using real coefficients. (solution in the pdf version of the book)
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.



