2.4: Convergence
( \newcommand{\kernel}{\mathrm{null}\,}\)
Figure II.5 shows a lens made of glass of refractive index 1.50. To the left of the lens is air (refractive index 1.00). To the right of the lens is water (refractive index 1.33). A converging beam of light is incident upon the lens directed toward a virtual object O that is 60 cm from the lens. After refraction through the lens, the light converges to a real image I that is 20 cm from the lens.
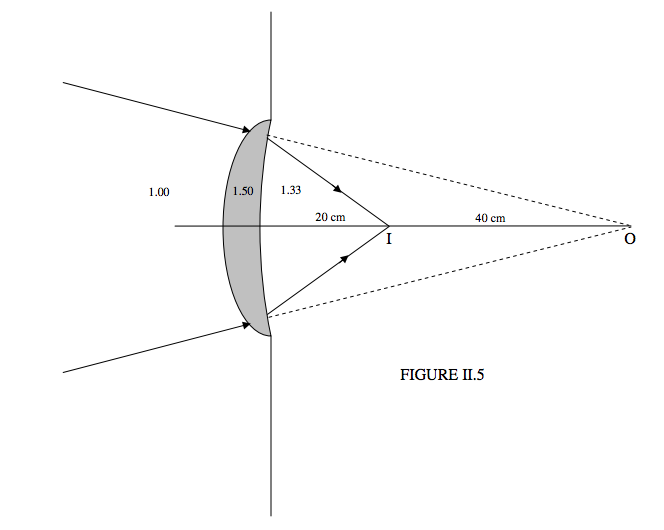
I am not at this stage going to ask you to calculate the radii of curvature of the lens. (You can’t – you need one more item of information.) I just want to use this diagram to define what I mean by convergence.
The convergence of the light at the moment when it is incident upon the lens is called the initial convergence C1, and it is defined as follows:
initial convergence=Refractive indexObjectdistance.
The convergence of the light at the moment when it leaves the lens is called the final convergence C2, and it is defined as follows:
final convergence=Refractive indexImagedistance.
Sign convention
- Converging light has positive convergence;
- Diverging light has negative convergence.
Example 2.4.1
Initial convergence = +1.0060=+0.01667 cm-1.
Final convergence = +1.3320=+0.06650 cm-1.
Notice that, before the light enters the lens, it is in a medium of refractive index 1.00. Thus the relevant refractive index is 1.00, even though the virtual object is in the water.


