5.4: Rotation Operators in Spin Space
- Page ID
- 1207
Let us, for the moment, forget about the spatial position of the particle, and concentrate on its spin state. A general spin state \( A\) is represented by the ket
Thus, after rotation, the ket \( \vert A_R\rangle = T_z({\mit\Delta}\varphi)\, \vert A\rangle.\)
To demonstrate that the operator \ref{440} really does rotate the spin of the system, let us consider its effect on \( \langle S_x\rangle \rightarrow \langle A_R\vert \,S_x\, \vert A_R \rangle = \langle A\vert \,T_z^{\dag }\, S_x \,T_z \,\vert A\rangle.\)
Thus, we need to compute
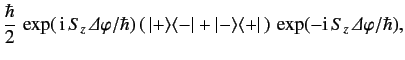
or
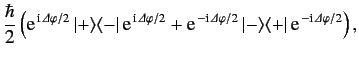
which reduces to
where \( \lambda\) a real parameter. The proof of this lemma is left as an exercise. Applying the Baker-Hausdorff lemma to Equation \ref{443}, we obtain
![$ S_x + \left(\frac{{\rm i}\,{\mit\Delta}\varphi}{\hbar}\right) [S_...
...\frac{{\rm i}\,{\mit\Delta}\varphi}{\hbar}\right)^2 [S_z, [S_z, S_x]] + \cdots,$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1090.png)
which reduces to
![$ S_x\left[ 1- \frac{({\mit\Delta}\varphi)^2}{2!} + \frac{({\mit\De...
...{\mit\Delta}\varphi)^3}{3!}+ \frac{({\mit\Delta}\varphi)^5}{5!} +\cdots\right],$](http://farside.ph.utexas.edu/teaching/qm/lectures/img1091.png)
or
under the action of the rotation operator \ref{440}. It is straightforward to show that
because \( {\bf S}\) by an angle \( z\) -axis. In fact, the expectation value of the spin operator behaves like a classical vector under rotation:
Consider the effect of the rotation operator \ref{440} on the state ket \ref{439}. It is easily seen that
Consider a rotation by \( \vert A\rangle \rightarrow T_z(2\pi)\,\vert A\rangle = -\vert A\rangle.\)
Note that a ket rotated by \( 4\pi\) radians is needed to transform a ket into itself. The minus sign does not affect the expectation value of \( {\bf S}\) is sandwiched between \( \vert A\rangle\), both of which change sign. Nevertheless, the minus sign does give rise to observable consequences, as we shall see presently.
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


