9.2: Fundamental

Consider time-independent scattering theory, for which the Hamiltonian of the system is written

$H_0$ is the Hamiltonian of a free particle of mass $H_0 = \frac{p^2}{2\,m},$ $\ref{911}$

and $\vert\phi\rangle$ be an energy eigenket of $H_0\, \vert\phi\rangle = E\, \vert\phi\rangle,$ $\ref{912}$

whose wavefunction $\phi({\bf x}')$ . This state is assumed to be a plane wave state or, possibly, a spherical wave state. Schrödinger's equation for the scattering problem is

$\vert\psi\rangle$ is an energy eigenstate of the total Hamiltonian whose wavefunction $\psi({\bf x}')$ . In general, both $H_0+H_1$ have continuous energy spectra: i.e., their energy eigenstates are unbound. We require a solution of Equation $\ref{913}$ that satisfies the boundary condition $H_1\rightarrow 0$ . Here, $(\nabla^2 + k^2)\,\psi({\bf x}) = \frac{2\,m}{\hbar^2}\, \langle {\bf x} \vert\,H_1\,\vert \psi\rangle,$ $\ref{914}$

where

$\psi({\bf x}) = \phi({\bf x}) + \frac{2\,m}{\hbar^2} \int d^3 x'\,G({\bf x}, {\bf x}') \,\langle {\bf x}' \vert\,H_1\,\vert\psi\rangle,$ $\ref{916}$

where

$\vert\psi\rangle \rightarrow \vert\phi\rangle$ as $G({\bf x}, {\bf x}') = -\frac{\exp(\pm {\rm i}\,k\, \vert{\bf x} - {\bf x}'\vert\,)}{4\pi\,\vert{\bf x} - {\bf x}'\vert}.$ $\ref{918}$

Thus, Equation $\ref{916}$ becomes

$\ref{919}$

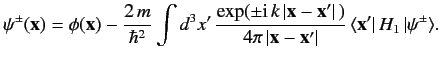Let us suppose that the scattering Hamiltonian, $\langle {\bf x}'\vert\,H_1\,\vert{\bf x}\rangle = V({\bf x})\, \delta({\bf x} -{\bf x}').$ $\ref{920}$

We can write

$\ref{921}$

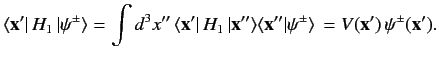Thus, the integral equation $\ref{919}$ simplifies to

$\ref{922}$

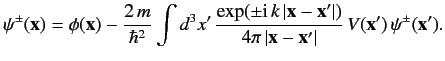Suppose that the initial state ${\bf k}$ (i.e., a stream of particles of definite momentum $\vert{\bf k}\rangle$ . The associated wavefunction takes the form

$\langle {\bf x} \vert {\bf k}\rangle = \frac{ \exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) }{(2\pi)^{3/2}}.$ $\ref{923}$

The wavefunction is normalized such that

$\ref{924}$

Suppose that the scattering potential ${\bf x} = {\bf0}$ ). Let us calculate the wavefunction $r\gg r'$ . It is easily demonstrated that

$r'/r$ , where

$r=\vert{\bf x}\vert$ and ${\bf k}' = k\,{\bf e}_r.$ $\ref{927}$

Clearly, ${\bf k}'$ is the wavevector for particles that possess the same energy as the incoming particles (i.e., $\exp(\pm {\rm i}\, k\,\vert{\bf x} - {\bf x}' \vert\,) \simeq \exp(\pm {\rm i}\, k \,r) \exp(\mp {\rm i}\, {\bf k}' \cdot {\bf x}').$ $\ref{928}$

In the large-$r$ limit, Equation $\ref{922}$ reduces to

$\ref{929}$

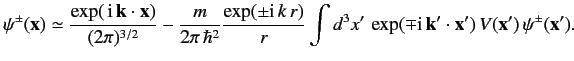The first term on the right-hand side is the incident wave. The second term represents a spherical wave centred on the scattering region. The plus sign (on $\psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left[\exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) + \frac{\exp(\,{\rm i}\,k\,r)}{r} f({\bf k}', {\bf k}) \right],$ $\ref{930}$

where

$\ref{931}$

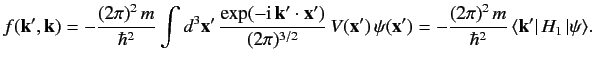Let us define the differential cross-section, $d{\mit\Omega}$ , divided by the incident flux of particles. Recall, from Chapter 3, that the probability current (i.e., the particle flux) associated with a wavefunction ${\bf j} = \frac{\hbar}{m}\, {\rm Im}(\psi^\ast\, \nabla \psi).$ $\ref{932}$

Thus, the probability flux associated with the incident wavefunction,

${\bf j}_{\rm inc} = \frac{\hbar}{(2\pi)^{3}\,m} \,{\bf k}.$ $\ref{934}$

Likewise, the probability flux associated with the scattered wavefunction,

${\bf j}_{\rm sca}=\frac{\hbar}{(2\pi)^{3}\,m} \frac{\vert f( {\bf k}', {\bf k})\vert^{\,2}}{r^2} \, k\, {\bf e}_r.$ $\ref{936}$

Now,

$\frac{d\sigma}{d {\mit\Omega}} = \vert f({\bf k}', {\bf k})\vert^{\,2}.$ $\ref{938}$

Thus, $\hbar\,{ \bf k}$ to be scattered into states whose momentum vectors are directed in a range of solid angles $\hbar\,{ \bf k}'$ . Note that the scattered particles possess the same energy as the incoming particles (i.e., $k'=k$ ). This is always the case for scattering Hamiltonians of the form specified in Equation $\ref{920}$.

Contributors

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  $\newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$