11.5: Electron Spin

Last updated
Save as PDF
Share
1. Share
2. Share
3. Tweet

According to Equation (1132), the relativistic Hamiltonian of an electron in an electromagnetic field is

$\displaystyle H =-e\,\phi + c\,$ $\displaystyle \mbox{\boldmath$\alpha$}$ $\displaystyle \cdot({\bf p}+e\,{\bf A})+ \beta\,m_e\,c^2.$

(1185)

Hence,

$\displaystyle \left(\frac{H}{c}+\frac{e}{c}\,\phi\right)^2 = \left[\mbox{\boldm... ...mbox{\boldmath$\alpha$}\cdot({\bf p}+e\,{\bf A})\right]^{\,2} + m_e^{\,2}\,c^2,$

(1186)

where use has been made of Equations (1118) and (1119). Now, we can write

$\displaystyle \alpha_i = \gamma^5\,\Sigma_i,$

(1187)

for , where

$\displaystyle \gamma^5 = \left(\begin{array}{cc} 0& 1\\ [0.5ex]1 & 0\end{array}\right),$

(1188)

and

$\displaystyle \Sigma_i = \left(\begin{array}{cc} \sigma_i& 0\\ [0.5ex]0& \sigma_i\end{array}\right).$

(1189)

Here, 0 and denote $2\times 2$ null and identity matrices, respectively, whereas the $\sigma_i$ are conventional $2\times 2$ Pauli matrices. Note that $\gamma^5\,\gamma^5=1$ , and

$\displaystyle [\gamma^5, \Sigma_i]=0.$

(1190)

It follows from (1186) that

$\displaystyle \left(\frac{H}{c}+\frac{e}{c}\,\phi\right)^2 = \left[\mbox{\boldmath$\Sigma$}\cdot({\bf p}+e\,{\bf A})\right]^{\,2} + m_e^{\,2}\,c^2.$

(1191)

Now, a straightforward generalization of Equation (508) gives

$\displaystyle ($ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle \cdot {\bf a} ) \,($ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle \cdot {\bf b}) = {\bf a} \cdot {\bf b} +{\rm i}\,$ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle \cdot ({\bf a} \times {\bf b}),$

(1192)

where ${\bf a}$ and ${\bf b}$ are any two three-dimensional vectors that commute with $\Sigma$ . It follows that

$\displaystyle \left[\mbox{\boldmath$\Sigma$}\cdot({\bf p}+e\,{\bf A})\right]^{\... ...,\mbox{\boldmath$\Sigma$}\cdot ({\bf p}+e\,{\bf A})\times ({\bf p}+e\,{\bf A}).$

(1193)

However,

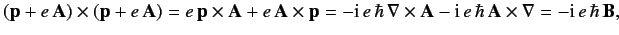$\displaystyle ({\bf p}+e\,{\bf A})\times ({\bf p}+e\,{\bf A}) = e\,{\bf p}\time... ...\bf A} -{ \rm i}\,e\,\hbar\,{\bf A}\times \nabla = -{\rm i}\,e\,\hbar\,{\bf B},$

(1194)

where ${\bf B} = \nabla\times {\bf A}$ is the magnetic field strength. Hence, we obtain

$\displaystyle \left(\frac{H}{c}+\frac{e}{c}\,\phi\right)^2 = ({\bf p}+e\,{\bf A})^2 + m_e^{\,2}\,c^2+e\,\hbar\,$ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle \cdot{\bf B}.$

(1195)

Consider the non-relativistic limit. In this case, we can write

$\displaystyle H = m_e\,c^2+ \delta H,$

(1196)

where $\delta H$ is small compared to $m_e\,c^2$ . Substituting into (1195), and neglecting $\delta H^{\,2}$ , and other terms involving $c^{\,-2}$ , we get

$\displaystyle \delta H\simeq -e\,\phi + \frac{1}{2\,m_e}\,({\bf p} + e\,{\bf A})^2 + \frac{e\,\hbar}{2\,m_e}\,$ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle \cdot{\bf B}.$

(1197)

This Hamiltonian is the same as the classical Hamiltonian of a non-relativistic electron, except for the final term. This term may be interpreted as arising from the electron having an intrinsic magnetic moment

$\displaystyle \mbox{\boldmath$\mu$}$ $\displaystyle = - \frac{e\,\hbar}{2\,m_e}\,$ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle .$

(1198)

In order to demonstrate that the electron's intrinsic magnetic moment is associated with an intrinsic angular momentum, consider the motion of an electron in a central electrostatic potential: i.e., $\phi=\phi(r)$ and ${\bf A}={\bf0}$ . In this case, the Hamiltonian (1185) becomes

$\displaystyle H = - e\,\phi(r) + c\,\gamma^5\,$ $\displaystyle \mbox{\boldmath$\Sigma$}$ $\displaystyle \cdot{\bf p} + \beta\,m_e\,c^2.$

(1199)

Consider the component of the electron's orbital angular momentum,

$\displaystyle L_x = y\,p_z-z\,p_y = {\rm i}\,\hbar\left(z\,\frac{\partial}{\partial y} - y\,\frac{\partial}{\partial z}\right).$

(1200)

The Heisenberg equation of motion for this quantity is

$\displaystyle {\rm i}\,\hbar\,\dot{L}_x = [L_x,H].$

(1201)

However, it is easily demonstrated that

$\displaystyle [L_x,r]$	$\displaystyle = 0,$	(1202)
$\displaystyle [L_x,p_x]$	$\displaystyle = 0,$	(1203)
$\displaystyle [L_x,p_y]$	$\displaystyle = {\rm i}\,\hbar\,p_z,$	(1204)
$\displaystyle [L_x,p_z]$	$\displaystyle = -{\rm i}\,\hbar\,p_y.$	(1205)

Hence, we obtain

$\displaystyle [L_x,H] = {\rm i}\,\hbar\,c\,\gamma^5\,(\Sigma_2\,p_z-\Sigma_3\,p_y),$

(1206)

which implies that

$\displaystyle \dot{L}_x = c\,\gamma^5\,(\Sigma_2\,p_z-\Sigma_3\,p_y).$

(1207)

It can be seen that is not a constant of the motion. However, the -component of the total angular momentum of the system must be a constant of the motion (because a central electrostatic potential exerts zero torque on the system). Hence, we deduce that the electron possesses additional angular momentum that is not connected with its motion through space. Now,

$\displaystyle {\rm i}\,\hbar\,\dot{\Sigma}_1= [\Sigma_1,H].$

(1208)

However,

$\displaystyle [\Sigma_1,\gamma^5]$	$\displaystyle = 0,$	(1209)
$\displaystyle [\Sigma_1,\Sigma_1]$	$\displaystyle = 0,$	(1210)
$\displaystyle [\Sigma_1,\Sigma_2]$	$\displaystyle =2\,{\rm i}\,\Sigma_3,$	(1211)
$\displaystyle [\Sigma_1,\Sigma_3]$	$\displaystyle =-2\,{\rm i}\,\Sigma_2,$	(1212)

$\displaystyle [\Sigma_1,H] = 2\,{\rm i}\,c\,\gamma^5\,(\Sigma_3\,p_y-\Sigma_2\,p_z),$

(1213)

which implies that

$\displaystyle \frac{\hbar}{2}\,\dot{\Sigma}_1 = -c\,\gamma^5\,(\Sigma_2\,p_z-\Sigma_3\,p_y).$

(1214)

Hence, we deduce that

$\displaystyle \dot{L}_x +\frac{\hbar}{2}\,\dot{\Sigma}_1 = 0.$

(1215)

Since there is nothing special about the direction, we conclude that the vector ${\bf L} + (\hbar/2)\,$ $\Sigma$ is a constant of the motion. We can interpret this result by saying that the electron has a spin angular momentum ${\bf S} = (\hbar/2)\,$ $\Sigma$ , which must be added to its orbital angular momentum in order to obtain a constant of the motion. According to (1198), the relationship between the electron's spin angular momentum and its intrinsic (i.e., non-orbital) magnetic moment is