1.17: Radiation Density and Irradiance
( \newcommand{\kernel}{\mathrm{null}\,}\)
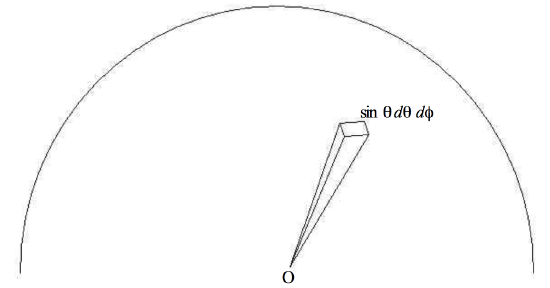
FIGURE I.7
Figure I.7 shows a hemisphere filled with radiation, the energy density being u J m−3. The motion of the photons is presumed to be isotropic, and all are moving at speed c. The centre of the base of the hemisphere, O, is being irradiated - i.e. bombarded with photons coming from all directions. How is the irradiance E at O related to the energy density? How much energy per unit area is arriving at O per unit time? I shall show that the answer is
E=uc/4.
Photons are arriving at O from all directions, but only a fraction
sinθδθδϕ4π
are coming from directions within the elemental solid angle between θ and θ+δθ and ϕ and ϕ+δϕ.
If there are n photons per unit volume, the rate at which photons (moving at speed c) are passing through an elemental area A at O from directions within the elemental solid angle sinθδθδϕ is
sinθδθδϕ4π×ncδAcosθ.
(This is because the elemental area presents a projected area δA cosθ to the photons arriving from that particular direction.)
The rate at which photons arrive per unit area (divide by δA) from the entire hemisphere above (integrate) is
∫2π0∫π/20ncsinθcosθdθdϕ4π
The rate at which energy arrives per unit area from the hemisphere above is
∫2π0∫π/20ucsinθcosθdθdϕ4π=uc/4,
which was to be demonstrated (Quod Erat Demonstrandum)
A more careful argument should convince the reader that it does not matter if all the photons do not carry the same energy. Just divide the population of photons into groups having different energies. The total energy is the sum of the energies of all the photons, whether these are equal or not.
I mentioned in section 1.12 that Stefan's law is sometimes written L=aT4, where a is Stefan's constant divided by π. It is also sometimes written u=a T4, and in this case a=4σ/c.


