1.7: Uniform Solid Tetrahedron, Pyramid and Cone
- Page ID
- 8346
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
A median of a tetrahedron is a line from a vertex to the centroid of the opposite face.
The four medians of a tetrahedron are concurrent at a point 3/4 of the way from a vertex to the centroid of the opposite face.
The centre of mass of a uniform solid tetrahedron is at the meet of the medians.
Theorem I can be derived by a similar vector geometric argument used for the plane triangle. It is slightly more challenging than for the plane triangle, and it is left as an exercise for the reader. I draw two diagrams (Figure I.14). One shows the point \( \text{C}_{1}\) that is 3/4 of the way from the vertex \( \text{A}\) to the centroid of the opposite face. The other shows the point \( \text{C}_{2}\) that is 3/4 of the way from the vertex \( \text{B}\) to the centroid of its opposite face. You should be able to show that
\( {\bf \text{C}_{1}}=({\bf\text{A+B+D}})/{4}\)
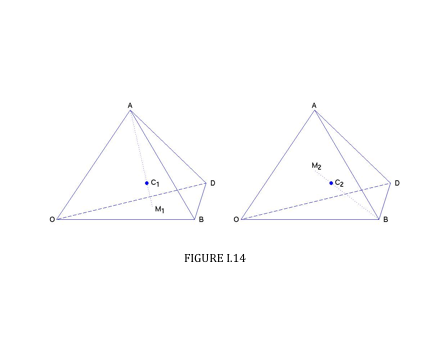
In fact this suffices to prove Theorem I, because, from the symmetry between \( {\bf \text{A}}\), \( {\bf \text{B}}\) and \( {\bf \text{D}}\), one is bound to arrive at the same expression for the three-quarter way mark on any of the four medians. But for reassurance you should try to show, from the second figure, that
\( {\bf \text{C}_{2}={\bf\text{A+B+D}})/{4}\)
The argument for Theorem II is easy, and is similar to the corresponding argument for plane triangles.
Pyramid.
A right pyramid whose base is a regular polygon (for example, a square) can be considered to be made up of several tetrahedra stuck together. Therefore the centre of mass is 3/4 of the way from the vertex to the mid point of the base.
Cone.
A right circular cone is just a special case of a regular pyramid in which the base is a polygon with an infinite number of infinitesimal sides. Therefore the centre of mass of a uniform right circular cone is 3/4 of the way from the vertex to the centre of the base.
We can also find the position of the centre of mass of a solid right circular cone by calculus. We can find its volume by calculus, too, but we'll suppose that we already know, from the theorem of Pappus, that the volume is \( \frac{1}{3}\) × base × height.
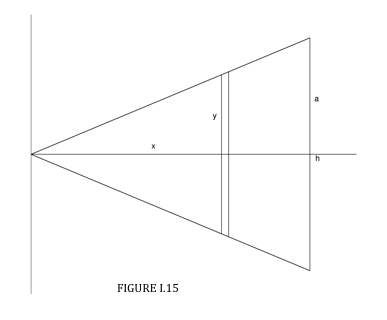
Consider the cone in Figure I.15, generated by rotating the line \( y= \frac{ax}{h} \) (between \( x = 0 \) and \( x = h \)) through 360o about the \( x \) axis. The radius of the elemental slice of thickness \( dx \) at \( x \) is \( \frac{ax}{h} \). Its volume is \( \frac{\pi a^{2}x^{2} \delta x }{h^2} \).
Since the volume of the entire cone is \( \frac{\pi a^{2}h}{3} \), the mass of the slice is
\(M \times \frac{ \pi a^{2}x^{2} \delta x}{h^{2}} \div \frac{\pi a^{2}h}{3} = \frac{3Mx^{2}\delta x}{h^3} \)
where \( M \) is the total mass of the cone. The first moment of mass of the elemental slice with respect to the \( y \) axis is \( \frac{3Mx^{3}dx}{h^{3}} \) .
The position of the centre of mass is therefore
\( \overline{x} = \frac{3}{h^{3}} \int_0^h x^3 dx = \frac{3}{4} h \)


