19.1: Introduction to Cycloids
- Page ID
- 7051
Let us set up a coordinate system \(Oxy\), and a horizontal straight line \(y = 2a\). We imagine a circle of diameter \(2a\) between the \(x\)-axis and the line \(y = 2a\), and initially the lowest point on the circle, P, coincides with the origin of coordinates O. We now allow the circle to roll counterclockwise without slipping on the line \(y = 2a\), so that the centre of the circle moves to the right. As the circle rolls on the line, the point P describes a curve, which is known as a cycloid.
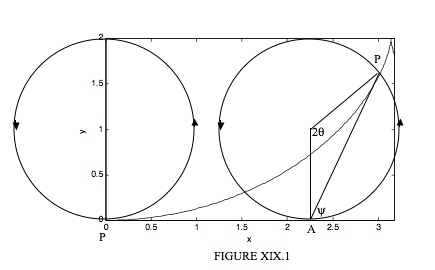
When the circle has rolled through an angle \(2\theta \), the centre of the circle has moved to the right by a horizontal distance \(2a \theta \), while the horizontal distance of the point P from the centre of the circle is \( a \sin 2 \theta \) and the vertical distance of the point \(P\) below the centre of the circle is \( a \cos 2 \theta \). Thus the coordinates of the point \(P\) are
\[ x = a(2 \theta + \sin 2 \theta) \label{19.1.1} \tag{19.1.1} \]
and
\[ y = a (1 - \cos 2 \theta ). \label{19.1.2}\tag{19.1.2} \]
Equations \(\ref{19.1.1}\) and \(\ref{19.1.2}\) are the parametric equations of the cycloid. Using a simple trigonometric identity, Equation \(\ref{19.1.2}\) can also be written
\[ y = 2a \sin^2 \theta . \label{19.1.3}\tag{19.1.3} \]
When the \(x\)-coordinate of P is 2.500\(a\), what (to four significant figures) is its \(y\)-coordinate?
Solution
We have to find \(2 \theta \) by solution of \( 2 \theta +\sin 2 \theta \). By Newton-Raphson iteration or otherwise, we find \(2 \theta \) = 0.931 599 201 radians, and hence y = 0.9316\(a\).


