20.4.2: The Couette Viscometer
- Page ID
- 8533
A cylindrical vessel of radius \(b\) contains the liquid whose viscosity is to be measured. A smaller, solid cylinder of radius \(a\) and length \(l\) is suspended from a torsion wire, whose torsion constant \(c\) is known, and is immersed in the liquid in the vessel, the two cylinders being coaxial. The vessel containing the liquid is spun about its axis at an angular speed \( \Omega\), thus setting the liquid in motion. This causes a viscous torque on the inner cylinder, which is therefore pulled round through an angle \( \phi \). When the restoring torque of the torsion wire \( c \phi \) is equal to the viscous torque, the system will be in equilibrium, and one can then calculate the viscosity \( \eta \) of the liquid. We shall refer to Figure XX.11. In the simple analysis given below, we suppose that the angular and linear speed and gradients are sufficiently small that the flow is nonturbulent. We also neglect the effects of viscous drag on the flat ends of the cylinder. Thus the diameter of the cylinder, in our analysis, must be much less than its length.
Incidentally, for a long time I thought that the word “couette” must be French for something. It is – it’s French for “feather bed” or for “pigtail”. But the Couette viscometer is actually named after a little-known nineteenth century French scientist, Maurice Couette.
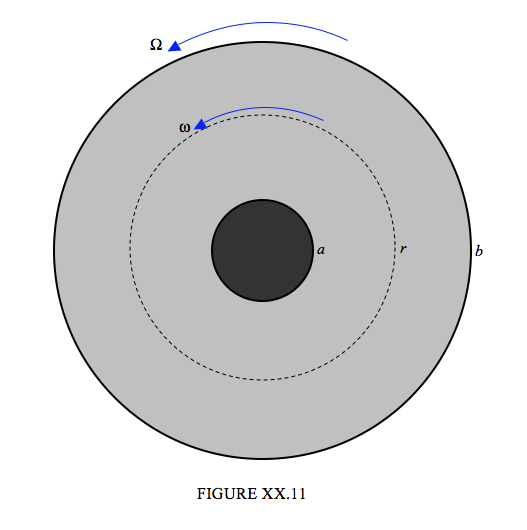
Let us calculate the viscous torque on the liquid within radius \( r \). Notice that, since we have a steady-state situation, this torque is independent of \(r\); in particular the torque on the liquid within radius \(r\) is the same as the torque (which we can measure with the torsion wire) on the inner cylinder. The area of the curved surface of the liquid within radius \(r\) is \( 2 \pi lr\). The viscous torque on this surface is \(r\) times \( \eta \) times the area times the transverse velocity gradient. But we have to be careful about this last term. If the whole body of the liquid were rotating as a solid body with angular speed \( \omega \), the speed at radius \(r\) would be \(r \omega \) and hence there would be a transverse velocity gradient equal to \( \omega \) − but no viscous drag! But the liquid is not, of course, rotating as a solid, and \( \omega \) (as well as \(v\)) is a function of \(r\). Since \(v = r \omega \), the velocity gradient is \( \frac{dv}{dr} = r \frac{d \omega}{dr} + \omega \) and the only part of this that goes into the expression for the viscous torque is the part \( r \frac{d \omega}{dr} \).Thus the expression for the torque on the liquid within radius r (and hence also on the inner cylinder) is
\[ \tau = r. \eta . 2 \pi r l. r \frac{d \omega}{dr}\tag{20.4.5}\label{eq:20.4.5} \]
That is,
\[ \frac{d \omega}{dr} = \frac{\tau}{2 \pi \eta l r^3} . \tag{20.4.6}\label{eq:20.4.6} \]
Integration from \( r = a, \omega = 0 \) to \( r = b, \omega = \Omega \) gives
\[ \tau = \frac{4 \pi \eta l \Omega a^2 b^2}{b^2 - a^2} \tag{20.4.7}\label{eq:20.4.7} \]
In equilibrium, this is equal to \(c \phi \), where \(c\) is the torsion constant of the suspension and \( \phi \) is the angle through which the inner cylinder has turned, and hence the viscosity can be determined. You should, as usual, check the dimensions of Equation \(\ref{eq:20.4.7}\).


