2.1: Mass
- Page ID
- 935
Change is impossible, claimed the ancient Greek philosopher Parmenides. His work was nonscientific, since he didn't state his ideas in a form that would allow them to be tested experimentally, but modern science nevertheless has a strong Parmenidean flavor. His main argument that change is an illusion was that something can't be turned into nothing, and likewise if you have nothing, you can't turn it into something. To make this into a scientific theory, we have to decide on a way to measure what “something” is, and we can then check by measurements whether the total amount of “something” in the universe really stays constant. How much “something” is there in a rock? Does a sunbeam count as “something?” Does heat count? Motion? Thoughts and feelings.
If you look at the table of contents of this book, you'll see that the first four chapters have the word “conservation” in them. In physics, a conservation law is a statement that the total amount of a certain physical quantity always stays the same. This chapter is about conservation of mass. The metric system is designed around a unit of distance, the meter, a unit of mass, the kilogram, and a time unit, the second. Numerical measurement of distance and time probably date back almost as far into prehistory as counting money, but mass is a more modern concept. Until scientists figured out that mass was conserved, it wasn't obvious that there could be a single, consistent way of measuring an amount of matter, hence jiggers of whiskey and cords of wood. You may wonder why conservation of mass wasn't discovered until relatively modern times, but it wasn't obvious, for example, that gases had mass, and that the apparent loss of mass when wood was burned was exactly matched by the mass of the escaping gases.
Once scientists were on the track of the conservation of mass concept, they began looking for a way to define mass in terms of a definite measuring procedure. If they tried such a procedure, and the result was that it led to nonconservation of mass, then they would throw it out and try a different procedure. For instance, we might be tempted to define mass using kitchen measuring cups, i.e., as a measure of volume. Mass would then be perfectly conserved for a process like mixing marbles with peanut butter, but there would be processes like freezing water that led to a net increase in mass, and others like soaking up water with a sponge that caused a decrease. If, with the benefit of hindsight, it seems like the measuring cup definition was just plain silly, then here's a more subtle example of a wrong definition of mass. Suppose we define it using a bathroom scale, or a more precise device such as a postal scale that works on the same principle of using gravity to compress or twist a spring. The trouble is that gravity is not equally strong all over the surface of the earth, so for instance there would be nonconservation of mass when you brought an object up to the top of a mountain, where gravity is a little weaker.
Although some of the obvious possibilities have problems, there do turn out to be at least two approaches to defining mass that lead to its being a conserved quantity, so we consider these definitions to be “right” in the pragmatic sense that what's correct is what's useful.
One definition that works is to use balances, but compensate for the local strength of gravity. This is the method that is used by scientists who actually specialize in ultraprecise measurements. A standard kilogram, in the form of a platinum-iridium cylinder, is kept in a special shrine in Paris. Copies are made that balance against the standard kilogram in Parisian gravity, and they are then transported to laboratories in other parts of the world, where they are compared with other masses in the local gravity. The quantity defined in this way is called gravitational mass.

Figure b: A measurement of gravitational mass: the sphere has a gravitational mass of five kilograms.
A second and completely different approach is to measure how hard it is to change an object's state of motion. This tells us its inertial mass. For example, I'd be more willing to stand in the way of an oncoming poodle than in the path of a freight train, because my body will have a harder time convincing the freight train to stop. This is a dictionary-style conceptual definition, but in physics we need to back up a conceptual definition with an operational definition, which is one that spells out the operations required in order to measure the quantity being defined. We can operationalize our definition of inertial mass by throwing a standard kilogram at an object at a speed of 1 m/s (one meter per second) and measuring the recoiling object's velocity. Suppose we want to measure the mass of a particular block of cement. We put the block in a toy wagon on the sidewalk, and throw a standard kilogram at it. Suppose the standard kilogram hits the wagon, and then drops straight down to the sidewalk, having lost all its velocity, and the wagon and the block inside recoil at a velocity of 0.23 m/s. We then repeat the experiment with the block replaced by various numbers of standard kilograms, and find that we can reproduce the recoil velocity of 0.23 m/s with four standard kilograms in the wagon. We have determined the mass of the block to be four kilograms.1 Although this definition of inertial mass has an appealing conceptual simplicity, it is obviously not very practical, at least in this crude form. Nevertheless, this method of collision is very much like the methods used for measuring the masses of subatomic particles, which, after all, can't be put on little postal scales!

Figure c: A measurement of inertial mass: the wagon recoils with the same velocity in experiments 1 and 2, establishing that the inertial mass of the cement block is four kilograms.
Astronauts spending long periods of time in space need to monitor their loss of bone and muscle mass, and here as well, it's impossible to measure gravitational mass. Since they don't want to have standard kilograms thrown at them, they use a slightly different technique (figures d and e). They strap themselves to a chair which is attached to a large spring, and measure the time it takes for one cycle of vibration.
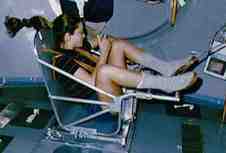
Figure d (left): The time for one cycle of vibration is related to the object's inertial mass.
Figure e (right): Astronaut Tamara Jernigan measures her inertial mass aboard the Space Shuttle.
1.1.1 Problem-solving techniques
How do we use a conservation law, such as conservation of mass, to solve problems? There are two basic techniques.
As an analogy, consider conservation of money, which makes it illegal for you to create dollar bills using your own inkjet printer. (Most people don't intentionally destroy their dollar bills, either!) Suppose the police notice that a particular store doesn't seem to have any customers, but the owner wears lots of gold jewelry and drives a BMW. They suspect that the store is a front for some kind of crime, perhaps counterfeiting. With intensive surveillance, there are two basic approaches they could use in their investigation. One method would be to have undercover agents try to find out how much money goes in the door, and how much money comes back out at the end of the day, perhaps by arranging through some trick to get access to the owner's briefcase in the morning and evening. If the amount of money that comes out every day is greater than the amount that went in, and if they're convinced there is no safe on the premises holding a large reservoir of money, then the owner must be counterfeiting. This inflow-equals-outflow technique is useful if we are sure that there is a region of space within which there is no supply of mass that is being built up or depleted.
| Example 1: A stream of water |
|---|
| If you watch water flowing out of the end of a hose, you'll see that the stream of water is fatter near the mouth of the hose, and skinnier lower down. This is because the water speeds up as it falls. If the cross-sectional area of the stream was equal all along its length, then the rate of flow (kilograms per second) through a lower cross-section would be greater than the rate of flow through a cross-section higher up. Since the flow is steady, the amount of water between the two cross-sections stays constant. Conservation of mass therefore requires that the cross-sectional area of the stream shrink in inverse proportion to the increasing speed of the falling water.
f / Example 1. |
self-check:
Suppose the you point the hose straight up, so that the water is rising rather than falling. What happens as the velocity gets smaller? What happens when the velocity becomes zero?
(answer in the back of the PDF version of the book)
How can we apply a conservation law, such as conservation of mass, in a situation where mass might be stored up somewhere? To use a crime analogy again, a prison could contain a certain number of prisoners, who are not allowed to flow in or out at will. In physics, this is known as a closed system. A guard might notice that a certain prisoner's cell is empty, but that doesn't mean he's escaped. He could be sick in the infirmary, or hard at work in the shop earning cigarette money. What prisons actually do is to count all their prisoners every day, and make sure today's total is the same as yesterday's. One way of stating a conservation law is that for a closed system, the total amount of stuff (mass, in this chapter) stays constant.
| Example 2: Lavoisier and chemical reactions in a closed system |
|---|
| The French chemist Antoine-Laurent Lavoisier is considered the inventor of the concept of conservation of mass. Before Lavoisier, chemists had never systematically weighed their chemicals to quantify the amount of each substance that was undergoing reactions. They also didn't completely understand that gases were just another state of matter, and hadn't tried performing reactions in sealed chambers to determine whether gases were being consumed from or released into the air. For this they had at least one practical excuse, which is that if you perform a gas-releasing reaction in a sealed chamber with no room for expansion, you get an explosion! Lavoisier invented a balance that was capable of measuring milligram masses, and figured out how to do reactions in an upside-down bowl in a basin of water, so that the gases could expand by pushing out some of the water. In a crucial experiment, Lavoisier heated a red mercury compound, which we would now describe as mercury oxide (HgO), in such a sealed chamber. A gas was produced (Lavoisier later named it “oxygen”), driving out some of the water, and the red compound was transformed into silvery liquid mercury metal. The crucial point was that the total mass of the entire apparatus was exactly the same before and after the reaction. Based on many observations of this type, Lavoisier proposed a general law of nature, that mass is always conserved. (In earlier experiments, in which closed systems were not used, chemists had become convinced that there was a mysterious substance, phlogiston, involved in combustion and oxidation reactions, and that phlogiston's mass could be positive, negative, or zero depending on the situation!)
a / Portrait of Monsieur Lavoisier and His Wife, by Jacques-Louis David, 1788. Lavoisier invented the concept of conservation of mass. The husband is depicted with his scientific apparatus, while in the background on the left is the portfolio belonging to Madame Lavoisier, who is thought to have been a student of David's. |
1.1.2 Delta notation
A convenient notation used throughout physics is \(\Delta\), the uppercase Greek letter delta, which indicates “change in” or “after minus before.” For example, if \(b\) represents how much money you have in the bank, then a deposit of $100 could be represented as $\Delta{}b=$100$. That is, the change in your balance was $100, or the balance after the transaction minus the balance before the transaction equals $100. A withdrawal would be indicated by \(\Delta{}b\lt0\). We represent “before” and “after” using the subscripts \(i\) (initial) and \(f\) (final), e.g., \(\Delta{}b=b_f-b_i\). Often the delta notation allows more precision than English words. For instance, “time” can be used to mean a point in time (“now's the time”), \(t\), or it could mean a period of time (“the whole time, he had spit on his chin”), \(\Delta{}t\).
This notation is particularly convenient for discussing conserved quantities. The law of conservation of mass can be stated simply as \(\Delta{}m=0\), where \(m\) is the total mass of any closed system.
self-check:
If \(x\) represents the location of an object moving in one dimension, then how would positive and negative signs of \(\Delta{}x\) be interpreted?
(answer in the back of the PDF version of the book)
Discussion Questions
If an object had a straight-line \(x-t\) graph with \(\Delta x=0\) and \(\Delta t\ne0\), what would be true about its velocity? What would this look like on a graph? What about \(\Delta t=0\) and \(\Delta x\ne0\)?
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.




