12.5: The Onset of Turbulence
- Page ID
- 1575
Learning Objectives
By the end of this section, you will be able to:
- Calculate Reynolds number.
- Use the Reynolds number for a system to determine whether it is laminar or turbulent.
Sometimes we can predict if flow will be laminar or turbulent. We know that flow in a very smooth tube or around a smooth, streamlined object will be laminar at low velocity. We also know that at high velocity, even flow in a smooth tube or around a smooth object will experience turbulence. In between, it is more difficult to predict. In fact, at intermediate velocities, flow may oscillate back and forth indefinitely between laminar and turbulent.
An occlusion, or narrowing, of an artery, such as shown in Figure \(\PageIndex{1}\), is likely to cause turbulence because of the irregularity of the blockage, as well as the complexity of blood as a fluid. Turbulence in the circulatory system is noisy and can sometimes be detected with a stethoscope, such as when measuring diastolic pressure in the upper arm’s partially collapsed brachial artery. These turbulent sounds, at the onset of blood flow when the cuff pressure becomes sufficiently small, are called Korotkoff sounds. Aneurysms, or ballooning of arteries, create significant turbulence and can sometimes be detected with a stethoscope. Heart murmurs, consistent with their name, are sounds produced by turbulent flow around damaged and insufficiently closed heart valves. Ultrasound can also be used to detect turbulence as a medical indicator in a process analogous to Doppler-shift radar used to detect storms.
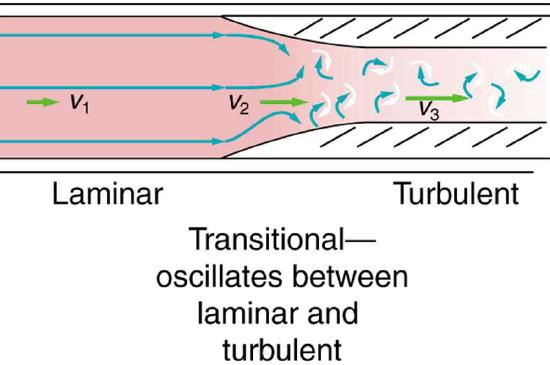
An indicator called the Reynolds number \(N_R\) can reveal whether flow is laminar or turbulent. For flow in a tube of uniform diameter, the Reynolds number is defined as
\[ \underbrace{N_R = \dfrac{2\rho vr}{\eta}}_{\text{flow in tube}}\]
where \(\rho\) is the fluid density, \(v\) its speed, \(\eta\) its viscosity, and \(r\) the tube radius. The Reynolds number is a unitless quantity. Experiments have revealed that \(N_R\) is related to the onset of turbulence. For \(N_R\) below about 2000, flow is laminar. For \(N_R\) above about 3000, flow is turbulent. For values of \(N_R\) between about 2000 and 3000, flow is unstable—that is, it can be laminar, but small obstructions and surface roughness can make it turbulent, and it may oscillate randomly between being laminar and turbulent. The blood flow through most of the body is a quiet, laminar flow. The exception is in the aorta, where the speed of the blood flow rises above a critical value of 35 m/s and becomes turbulent.
Example \(\PageIndex{1}\): Is This Flow Laminar or Turbulent?
Calculate the Reynolds number for flow in the needle considered in Example 12.8 to verify the assumption that the flow is laminar. Assume that the density of the saline solution is \(1025 \, kg/m^3\).
Strategy
We have all of the information needed, except the fluid speed \(v\), which can be calculated from \(\overline{v} = Q/A = 1.70 \, m/s\) (verification of this is in this chapter’s Problems and Exercises).
Solution
Entering the known values into \(N_R = \frac{2\rho vr}{\eta}\) gives
\[N_R = \dfrac{2\rho vr}{\eta}\]
\[= \dfrac{2(1025 \, kg/m^3)(1.70 \, m/s)(0.150 \times 10^{-3} \, m)}{1.00 \times 10^{-3} \, N\cdot s/m^2}\]
\[= 523.\]
Discussion
Since \(N_R\) is well below 2000, the flow should indeed be laminar.
Take-Home Experiment: Inhalation
Under the conditions of normal activity, an adult inhales about 1 L of air during each inhalation. With the aid of a watch, determine the time for one of your own inhalations by timing several breaths and dividing the total length by the number of breaths. Calculate the average flow rate \(Q\) of air traveling through the trachea during each inhalation.
The topic of chaos has become quite popular over the last few decades. A system is defined to be chaotic when its behavior is so sensitive to some factor that it is extremely difficult to predict. The field of chaos is the study of chaotic behavior. A good example of chaotic behavior is the flow of a fluid with a Reynolds number between 2000 and 3000. Whether or not the flow is turbulent is difficult, but not impossible, to predict—the difficulty lies in the extremely sensitive dependence on factors like roughness and obstructions on the nature of the flow. A tiny variation in one factor has an exaggerated (or nonlinear) effect on the flow. Phenomena as disparate as turbulence, the orbit of Pluto, and the onset of irregular heartbeats are chaotic and can be analyzed with similar techniques.
Summary
- The Reynolds number \(N_R\) can reveal whether flow is laminar or turbulent. It is \[N_R = \dfrac{2\rho vr}{\eta}.\]
- For \(N_R\) below about 2000, flow is laminar. For \(N_R\) above about 3000, flow is turbulent. For values of \(N_R\) between 2000 and 3000, it may be either or both.
Glossary
- Reynolds number
- a dimensionless parameter that can reveal whether a particular flow is laminar or turbulent


