02. Analysis Tools
- Page ID
- 553
Applying the Impulse-Momentum Relation to a Single Object
Let’s investigate the following scenario:
A boy pulls a 30 kg sled, including the mass of his kid brother, along ice. The boy pulls on the tow rope, oriented at 600above horizontal, with a force of 110 N until his kid brother begins to cry. Like clockwork, his brother always cries upon reaching a speed of 2.0 m/s. The frictional coefficient is (0.20,0.15).
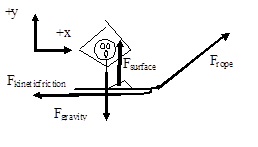
Event 1: The instant before the sled begins to move.
Event 2: The instant the sled reaches 2.0 m/s.
Let’s apply the impulse-momentum relations to see what they reveal about the situation.
Applying impulse-momentum separately in the x- and y-directions yields:
x-direction y-direction
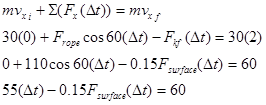
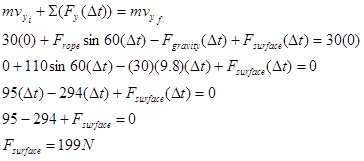
Substituting the value for the force of the surface into the x-equation,
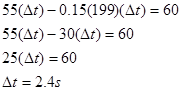
The kid brother begins to cry after only 2.4 s.
Applying the Work-Energy Relation to a Single Object
What will the work-energy relation tell us about the same scenario?
A boy pulls a 30 kg sled, including the mass of his kid brother, along ice. The boy pulls on the tow rope, oriented at 600above horizontal, with a force of 110 N until his kid brother begins to cry. Like clockwork, his brother always cries upon reaching a speed of 2.0 m/s. The frictional coefficient is (0.20,0.15).
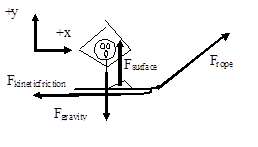
Event 1: The instant before the sled begins to move.
Event 2: The instant the sled reaches 2.0 m/s.
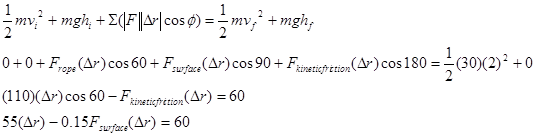
Notice that the force of the surface does no work, the force of the rope does positive work, and the force of friction does negative work. Each of these terms should make sense if you remember that work is the transfer of energy into (positive) or out of (negative) the system of interest. Also recall that in this form of the work-energy relation we conceptualize gravity as a source of potential energy, not as a force that does work.
Using the result for the force of the surface determined in the first example, Fsurface= 199 N, gives:
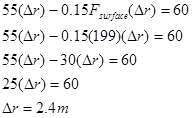
The kid brother begins to cry after traveling 2.4 m.


