20.2.3: Capillary Rise
( \newcommand{\kernel}{\mathrm{null}\,}\)
When the lower end of a narrow capillary tube is immersed in a liquid, the liquid inside the tube rises a little above the level of the liquid outside. If is then very simple to calculate how far the liquid rises in terms of the surface tension, the angle of contact and the inside radius of the tube. See Figure XX.5.
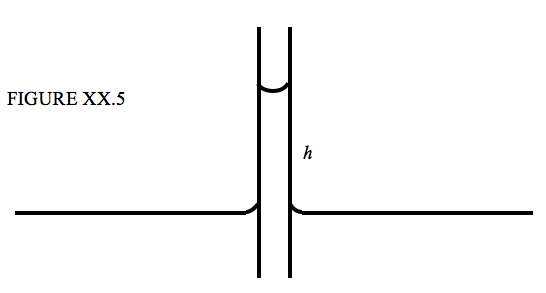
The upward force due to surface tension is 2πaγcosθ where a is the inside radius of the tube, and, if we neglect the very small mass of the liquid in the meniscus (the curved surface at the top of the liquid column), the weight of the liquid column is πa2hρg, and therefore
h=2γcosθρga.
Of course if θ is obtuse (as with mercury in contact with glass), h will be negative, and the level of the mercury in the tube will be below the outside level.


