1.2: Boyle's Law and the Law of Atmospheres
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}We’ve discussed the concept of pressure in the previous lecture, introduced units of pressure (Newtons per square meter, or Pascals, and the more familiar pounds per square inch) and noted that a fluid in a container exerts pressure on all the walls, vertical as well as horizontal—if a bit of wall is removed, the fluid will squirt out.
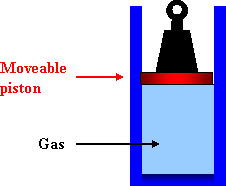
Everyone knows that although water (like other liquids) is pretty much incompressible, air is compressible—you can squeeze a small balloon to a noticeably smaller volume with your hands, and you can push in a bicycle pump to some extent even if you block the end so no air escapes. . Boyle was the first person to make a quantitative measurement of how the volume of a fixed amount of air went down as the pressure increased.
One might imagine doing the experiment with gas in a cylinder as in the diagram here, putting on different weights and measuring the volume of the gas. Once the piston is at rest, the pressure of the gas multiplied by the area of the piston would just balance the weight of the piston plus the added weight, so the pressure is easy to find.
But there is one tricky point here: if the gas is compressed fairly rapidly—such as by adding a substantial weight, so the piston goes down suddenly—the gas heats up. Then, as the heat escapes gradually through the walls of the cylinder, the gas gradually settles into an even smaller volume.
Boyle’s idea was to find out how the volume of the gas varied with outside pressure if the temperature of the gas stayed the same. So, if he’d done his experiment with the cylinder pictured above, he would have had to wait quite a time between volume measurements to be sure the gas was back to room temperature.
But Boyle didn’t use a piston and cylinder. He did the experiment in 1662. Possibly the gun barrels manufactured at the time would have worked, with a greasy piston (I’m not sure) but he found a very elegant alternative: he trapped the air using mercury in a closed glass tube, and varied the pressure as explained below (in his own words).
He found a simple result: if the pressure was doubled, at constant temperature, the gas shrank to half its previous volume. If the pressure was tripled, it went to one-third the original volume, and so on. That is, for pressure P and volume V, at constant temperature T, PV = constant. This is Boyle’s Law.
After reviewing Boyle’s ingenious experiment, we shall see how Boyle’s Law is the key to understanding a central feature of the earth’s atmosphere: just how the density and pressure of air decreases with altitude. Of course, the temperature of the atmosphere also varies with height and weather, complicating the picture, but Boyle’s law gives us a very good start in analyzing the situation.
Boyle’s Experiment
Robert Boyle was born on 1627, the fourteenth child of the Earl of Cork, an Irish landowner. He wrote the account below in 1662. (It is from his book A Defense of the Doctrine Touching the Spring and Weight of the Air. I’ve added some notes in square brackets, which I hope clarify what’s going on. Regular brackets, ( ), are Boyle’s own.)
“We took then a long glass-tube, which, by a dexterous hand and the help of a lamp, [heating it so it softens] was in such a manner crooked at the bottom, that the part turned up was almost parallel to the rest of the tube [they bent it into the shape in the diagram] and the orifice of this shorter leg of the siphon (if I may so call the whole instrument) being hermetically sealed, the length of it was divided into inches (each of which was subdivided into eight parts) by a streight list of paper, which containing those divisions was carefully pasted all along it. Then putting in as much quicksilver as served to fill the arch or bended part of the siphon, that the mercury standing in a level might reach in the one leg to the bottom of the divided paper, and just to the same height of horizontal line in the other; we took care, by frequently inclining the tube, so that the air might freely pass from one leg into the other by the sides of the mercury (we took, I say, care) that the air at last included in the shorter cylinder should be of the same laxity with the rest of the air about it. [He means at the same pressure, that is, the normal atmospheric pressure.]
This done, we began to pour quicksilver into the longer leg of the siphon, which by its weight pressing up that in the shorter leg, did by degrees streighten [compress] the included air: and continuing this pouring in of quicksilver till the air in the shorter leg was by condensation reduced to take up by half the space it possessed before; we cast our eyes upon the longer leg of the glass, on which was likewise pasted a list of paper carefully divided into inches and parts, and we observed, not without delight and satisfaction, that the quicksilver in that longer part of the tube was twenty-nine inches higher than the other.”
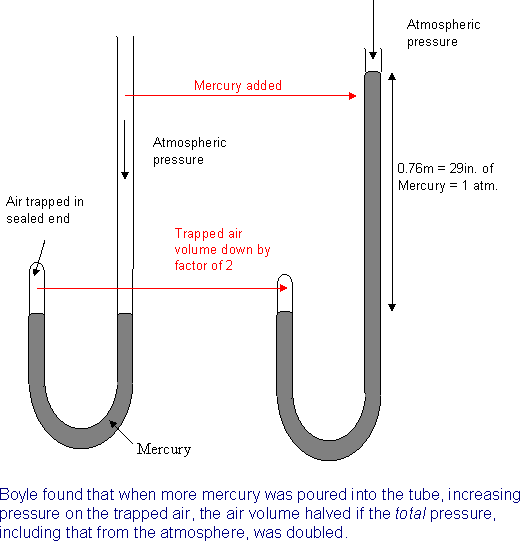
Boyle’s “delight and satisfaction” in that last sentence arose because he knew that the extra pressure exerted by the added twenty-nine inches of mercury was equal to an extra atmosphere, so the air trapped in the shorter tube had halved in volume when the pressure was doubled. He went on the repeat the experiment many times, with different heights of the column of mercury in the longer tube, and checking each day on the actual atmospheric pressure at the time of the experiment.
He established Boyle’s Law,
PV = const
for the range of pressures he used. It is important to note that in his experiments he allowed a long enough time between volume measurements for the trapped air to get back to room temperature.
The Law of Atmospheres: An Ocean of Water
First, a quick reminder of how we found the pressure variation with depth in an ocean of water at rest. We imagine isolating a small cylinder of water, with its axis vertical, and construct a free body diagram:
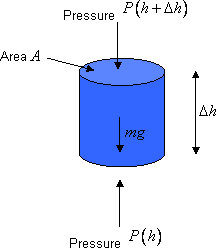
The pressure forces from the surrounding water acting on the curved sides obviously all cancel each other. So the only forces that count are the weight of the cylinder of water, and the pressure forces on the top and the bottom—that on the bottom being greater, since it must balance the pressure on the top plus the weight, since the cylinder is at rest.
Taking the cylinder to have cross-section area A, height \Delta h , and the water to have density \rho , the cylinder has volume A \Delta h , mass \rho A \Delta h , and therefore weight \rho A \Delta h g.
The pressure P is a function of height h above the bottom, P = P(h).
We’ve measured h here from the bottom of the ocean, because in the next section, we’ll apply the same analysis to the atmosphere, where we do live at the bottom of the “sea”.
The pressure on top of the cylinder exerts a downward force equal to pressure \, \times \, area = P(h+ \Delta h) A the bottom feels an upward pressure P(h) A ,
so since the total force must be zero,
P(h + \Delta h) A - P(h)A + \rho \, A \Delta H g = 0 .
This equation can be rearranged to:
\dfrac { P(h + \Delta h) - P(h)}{ \Delta h} = - \rho g. .
Recalling that the differential is defined by
\dfrac {df(x)}{dx} = lim \dfrac {f(x + \Delta x) - f(x)}{ \Delta x} ,
we see that this pressure equation in the limit \Delta h \rightarrow 0 becomes: \dfrac {dP(h)}{dh} = - \rho g .
Since \rho g is a constant, the solution is simple:
P(h) = - \rho g(h - h_0)
where we’ve written the constant of integration in the form \rho gh .
Notice the pressure in this ocean drops to zero at height h = h0 – obviously the surface! This means our formula describes water pressure in an ocean of depth h0, and is just a different way of writing that the pressure is \rho g times the depth below the surface. (We are subtracting off the atmospheric pressure acting down on the ocean’s surface from the air above it—we’re just considering the extra pressure from the weight of the water itself as we descend. Remember air pressure is the same as approximately thirty feet of water, so is a small correction in a real ocean)
An Ocean of Air - Law of Atmospheres
We now go through exactly the same argument for an “ocean of air”, drawing the same free body diagram for a small vertical cylinder, and arriving at the same differential equation,
\dfrac {dP(h)}{dh} = - \rho g .
But it does not have the same solution! The reason is that \rho , which we took to be constant for water (an excellent approximation), is obviously not constant for air. It is well known that the air thins out with increasing altitude.
The key to solving this equation is Boyle’s Law: for a given quantity of gas, it has the form PV = const. , but notice that means that if the pressure of the gas is doubled, the gas is compressed into half the space, so its density is also doubled.
So an alternative way to state Boyles law is
\rho (h) = CP(h)
where C is a constant (assuming constant temperature). Putting this in the differential equation:
\dfrac{ dP(h)}{dh} = - CP(h) g .
This equation can be solved (if this is news to you, see the footnote at end of this section):
P(h) = P_0e^{-C_gh} .
The air density decreases exponentially with height: this equation is the Law of Atmospheres.
This density decrease does not happen with water because water is practically incompressible. One analogy is to imagine the water to be like a tower of bricks, one on top of the other, and the air a tower of brick-shaped sponges, so the sponges at the bottom are squashed into much greater density—but this isn’t quite accurate, because at the top of the atmosphere, the air gets thinner and thinner without limit, unlike the sponges.
Footnote: Solving the Differential Equation
The equation is the same as \dfrac {df(x)}{dx} = af(x) , where a is a constant. If you are already familiar with the exponential function, and know that \dfrac {d}{dx}e^{ax} = ae^{ax} , you can see the equation is solved by the exponential function. Otherwise, the equation can be rearranged to \dfrac{df}{f} = adx , then integrated using \int \dfrac {df}{f} = ln f to give ln \, f(x) = ax + c , with c a constant of integration. Finally, taking the exponential of each side, using e^{hf(x)} = f(x) , gives f(x) = Ce^{ax} , where C = e^c .
Exercises
1. Atmospheric pressure varies from day to day, but 1 atm is defined as 1.01 x 105 Pa. Calculate how far upwards such a pressure would force a column of water in a “water barometer”.
2. The density of air at room temperature is about 1.29 kg/m3. Use this together with the definition of 1 atm above to find the constant C in the Law of Atmospheres written above. Use your result to estimate the atmospheric pressure on top of the Blue Ridge (say 4000 feet), Snowmass (11,000 feet) and Mount Everest (29,000 feet).
3. As a practical matter, how would you measure the density of air in a room? Actually, Galileo did this in the early 1600’s. Can you figure out how he managed to do it? (His result was off by a factor of two, but that was still pretty good!)
Contributors and Attributions
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


