2.3: Membrane Curvature

There is a large variety of complex shapes of cells and cell organelles found in nature, and understanding functions of the morphology and how it is produced has been an intriguing question and a challenge. For example, cells without internal membranes, such as prokaryotic cells and erythrocytes can take different shapes suited for their purposes. Spirochetes, a type of bacteria, has corkscrew shape which may be an advantage for penetration and packing into host cells while the biconcave disk-like shape of erythrocytes provides the optimal surface-to-volume ratio for the oxygen exchange between haemoglobin and the outside medium [4].

There are significant local differences in membrane curvature even within one single cell with internal membranes giving intercellular organelles a variety of shapes. Plasma membranes, organelle membranes of Golgi, endosome and endoplasmic reticulum (ER), as seen in Figure \(\PageIndex{1}\), all have varied curvature and their membrane curvature regularly goes through dynamic remodeling for their specific functions [1]. The shapes defined by the curvatures of their intercellular membranes of Golgi and ER, for example, maximize the surface area while keeping the internal volume low, which allows efficient and fast protein trafficking in and out of these organelles [4].

Figure \(\PageIndex{1}\) Local differences in membrane curvature in a cell [1].

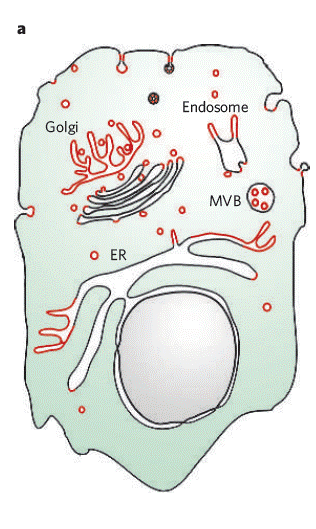
Conformation (Curvature and shape) of cellular or intercellular membranes consisting of semi-permeable phospholipid bilayers are actively modulated by the interaction between phospholipids, cholesterols and proteins. It is essential for living organisms to regulate membrane curvatures because this allows cells and organelles take specific shapes that are suitable for their functions, and processes, such as endocytosis and exocytosis depend, which are vital in living organisms, on membrane remodeling to sustain life and malfunction of the regulating system can lead to serious diseases [2, 3].

Definition of curvature

A biological membrane is commonly described as a two-dimensional surfaces, which spans a three-dimensional space. There are two curvatures that characterize the shape of a membrane at each point in space, and mathematically, they are called the principal curvatures and are expressed as c₁ and c₂ [4]. These curvatures are equal to the inverse values of the radii of curvature and Figure \(\PageIndex{2}\) shows how the radii are determined. Two different combinations of the curvatures are used to describe the shape of a membrane. One is as total curvature,

\[ J = c_1+c_2\]

and the other is Gaussian curvature

\[ K = c_1 \times c_2.\]

The basic membrane shapes and the corresponding total curvatures and Gaussian curvatures are indicated in Figure \(\PageIndex{3}\) [4]. Total curvature is a measure in terms of its "curvedness," torsion and direction and takes into account the 2- and 3-dimensional space while the Gaussian curvature is a measure of the "curvedness" a surface displays and is an intrinsic property of a membrane, which means that this measure does not change as long as the surface is not stretched nor compressed [4].

Figure \(\PageIndex{2}\) Determining membrane curvature [4].

As can be seen from Figure \(\PageIndex{3}\), curvatures can be positive or negative. For cellular membranes, positive or negative curvature is determined by curve directionality toward or away relative to the compartment or volume contained by the membrane [1]. Positive curvature builds a sphere while negative curvature is in the opposite direction, like at the neck of a vesicle budding.

The Helfrich theories allows calculation of bending energy required to produce these curvatures using two principal curvature values, c₁ and c₂, spontaneous curvature of a membrane, c₀, and the membrane bending modulus κ_b (Equation \ref{eq1}) [5]. Spontaneous curvature is intrinsic to lipid types and depending on their chemical compositions and structures, different lipids prefer different curvatures as further mentioned in Section 2. Typical value for bending modulus of a phospholipid membrane is about 10^-19 J and it can be measured using a technique called micropipette aspiration.

\[E_{bend} = \dfrac{1}{2} κ_b (c_1+c_2-c_0)^2 \label{eq1}\]

Figure \(\PageIndex{3}\) Basic membrane shapes [4].

Lipid Composition

Although many curvature-generating proteins have larger effects in membrane dynamics, lipid composition influences curvatures because the chemical properties of different lipid acyl chains or head groups favor different membrane curvatures [1]. Based on their preferred curvatures, also referred to as spontaneous curvatures, lipids can be classified into three types: type 0, type I, and type II (Figure \(\PageIndex{4}\)). Type 0 lipids such as phosphatidylcholines (DOPC) prefer no curvature and often form flat bilayers. Type I lipids are found in modified forms of DOPC where one fatty acid residue is removed, for example lyso-PC [5]. Their larger head groups relative to their long fatty acid chains lead to cone-shaped structure, inducing positive curvature, and therefore, formation of micelles [5]. Due to their smaller headgroups compared to their wider fatty acid chains, type II lipids such as phosphatidylethanolamine (PE) prefer negative curvature, and often form what is called H_II-phase.

Figure \(\PageIndex{4}\) The shapes of lipid molecules can induce spontaneous curvature on membranes [5].

In membranes with multiple lipid components, lipids can respond to curvature by concentrating in domains of curvature that they prefer [1, 6]. Baumgart et al. used freely suspended giant unilamellar vesicles (GUVs), consisting of ternary mixture of the lipids sphingomyelin, dioleoylphophatidylcholine (DOPC) and cholesterol, to directly observe this correlation between domain composition and local membrane curvature. (Figure5) In there experiments, they observed the lipid membrane of this composition phase separated into a short-range order phase (L_o), which favored lower curvature suggesting their higher membrane rigidity, and a disordered liquid phase (L_d), which favored higher curvature suggesting their lower membrane rigidity.

Figure \(\PageIndex{5}\) Structure of multicomponent vesicles [6].

Membrane Proteins

Proteins can generate membrane curvatures either by transporting lipids across the membrane or templating the membrane. Flippase is one protein known to transfer lipids from one leaflet to the other creating membrane asymmetry which leads to membrane curvatures. There are four types of proteins which act as mechanisms for templating membrane curvatures: transmembrane proteins, cytoskeletal proteins and microtubule motor activity, peripheral membrane proteins as scaffolds and amphipathic helices that are inserted into the bilayer [1].

Figure \(\PageIndex{6}\) Mechanisms of membrane deformation [1].

Transmembrane proteins such as ion channels, transporters and receptors that have a conical or inverted conical shape prefer curvatures that mold around their shapes, causing their associated membranes to bend. Extramembrane domains can play a role in generating membrane curvatures when there are not symmetric on both sides of the membranes [7, 8]. The membrane may bend away from the side with the largest extramembrane domain to avoid protein crowding on one side [8]. Transmembrane proteins can also oligomerize and form clusters and scaffold membranes leading to an even greater effect on local curvature [1, 7].

Generation of high membrane curvature structures often involve macroscopic scaffolding by cytoskeletal proteins and microtubule motor activity [7]. The cytoskeleton has a large role in maintaining membrane tension which affects membrane shape by connecting to the bilayer at regular intervals and providing an underlying scaffold [1, 7]. Active membrane pulling or pushing by molecular motors such as kinesins, dynein and myosin also induces membrane reorganization and supports some of the membrane curvatures that shape organelles [7, 9].

Peripheral membrane proteins can interact with membranes in a scaffold-like manner [1]. Dynamin family proteins, including classical dynamin and dynamin-related proteins, play active roles in membrane dynamics to catalyze membrane remodeling, such as in organelle division and vesicle invagination [1, 10]. Commonly, dynamin proteins interact with inositol lipids and self-assemble into oligomers that form helical structures to induce tubular membranes. Interestingly, cryo-EM data has shown that the yeast dynamin-related protein Dnm1 assembles into distinct helical structures, and in vitro liposome assays showed that Dnm1 constricts synthetic membranes [10]. These data further supported the role of this dynamin-related protein in membrane dynamics, in particular, for mitochondrial membrane division [10]. Oligomerized hydrophilic protein domains can generate curvatures through nanoscopic scaffolding. For example, coat proteins such as clathrin, COPI and COPII can influence membrane bending by polymerizing into curved structures. However, these proteins do not have direct associations with membrane and rely on adaptor proteins to link them to membranes [1, 7]. Another example of peripheral membrane scaffolding membranes is through BAR (Bin-Amphiphysin-Rvs) domains which are protein dimerization domains found in many proteins. They are banana-shaped which allow them to preferentially bind to concave membrane surfaces that are negatively-charged and function as a curvature-sensing protein.

Figure \(\PageIndex{7}\) BAR domain with low-curvature membrane and high-curvature membrane [1].

Proteins with amphipathic helices insert into bilayers to induce positive curvature [1]. Amphipathic helices are alpha helices with a charged, polar side and a hydrophobic side, allowing them to act like wedges to insert into one leaflet of the membrane. Commonly, these helices are not structured until inserted into a membrane where lipid headgroups are displaced and acyl chains are reoriented. For example, epsin is a protein involved in clathrin-coated pit formation in endocytosis that helps to drive membrane curvature by the insertion of its amphipathic helix (Figure \(\PageIndex{8}\)) [1].

Figure \(\PageIndex{8}\) Amphipathic helices and membrane curvature [1].

Functions of Dynamic Membrane Remodeling

The generation and maintenance of curvature is essential in eukaryotic life as they have trafficking and cellular functions. The formation of high-curvature transport intermediates is necessary for compartmentalization and the characteristic shapes of organelles are maintained by their membrane curvatures as shown in Figure \(\PageIndex{1}\) [7]. These organelles shapes are dynamic constantly going through changes in response to the needs of the cell.

For example, membrane scission, a processes involved in exocytosis and in generation of transport carriers, requires the localized and timely connection in trans of two bilayer membranes to separate an organelle from its membrane of origin. Members of the dynamin superfamily mainly drives membrane scission by oligomerizing at the neck of nascent vesicles and triggering fusion between the two lipid bilayers. This can cause the scission of th eneck and detachment of the vesicle. High local concentrations of hydrophobic insertions at the neck of constricted vesicle carriers supports the fission sf nascent membrane-trafficking vesicles by creating sufficient stress on the bilayer to favor scission in vesicles such as COPII vesicles [7].

References

1. McMahon, H. T.; Gallop, J. L. Membrane curvature and mechanisms of dynamic cell membrane remodeling. Nature, 2005, 438, 590- 596.
2. Sodt, A.; R. Paster. Molecular modeling of lipid membrane curvature induction by a peptide: More than simply shape. Biophysical Journal. 2014, 106, 1958-1969.
3. Baumgart, T.; Capraro, B. R.; Zhu, C.; Das, S. L. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu. Rev. Phys. Chem. 2011, 62, 483-506.
4. Zimmerberg, J.; Kozlov, M. M. How proteins produce cellular membrane curvature. Nature, 2005, 7, 9-19.
5. Phillips, R.; Kondev, J.; Theriot, J.; Garcia, H. G. Physical Biology of the Cell, 2013, Garland Science, Taylor & Francis Group, LLC: Abingdon, UK.
6. Baumgart, T.; Hess, S. T.; Webb, W. W. Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature, 2003, 425, 821-824.
7. McMahon, H. T.; Boucrot, E. Membrane curvature at a glance. J. Cell Sci. 2015, 128, 1065-1070.
8. Copic, A.; Latham, C. F.; Horlbeck, M. A; D'Accangelo, J. G.; Miller, E. A. ER cargo properties specify a requirement for COPII coat rigidity mediated by Sec 13p. Science, 2012, 335, 1359-1362.
9. Leduc, C.; Campas, O.; Joanny, J. F.; Prost, J.; Basserearu, P. Mechanism of membrane nanotube formation by molecular motors. Biochim. Biophys. Acta, 2010, 1798, 1418-1426.
10. Mears, J. A.; Lackner, L. L.; Fang, S.; Ingerman, E.; Nunnari, J.; Hinshaw, J. E. Conformational changes in Dnm1 support a contractile mechanism for mitochondrial fission. Nat. Struct. Mol. Biol. 2011, 18, 20-26.