2.2: Affine Properties of Lorentz Geometry (Part 1)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Parallelism and measurement
We think of a frame of reference as a body of measurements or possible measurements to be made by some observer. Ordered geometry lacks measure. The following argument shows that merely by adding a notion of parallelism to our geometry, we automatically gain a system of measurement.
We only expect Lorentz frames to be local, but we do need them to be big enough to cover at least some amount of spacetime. If Betty does an Eötvös experiment by releasing a pencil and a lead ball side by side, she is essentially trying to release them at the same event A, so that she can observe them later and determine whether their world-lines stay right on top of one another at point B. That was all that was required for the Eötvös experiment, but in order to set up a Lorentz frame we need to start dealing with objects that are not right on top of one another. Suppose we release two lead balls in two different locations, at rest relative to one another. This could be the first step toward adding measurement to our geometry, since the balls mark two points in space that are separated by a certain distance, like two marks on a ruler, or the goals at the ends of a soccer field. Although the balls are separated by some finite distance, they are still close enough together so that if there is a gravitational field in the area, it is very nearly the same in both locations, and we expect the distance defined by the gap between them to stay the same. Since they are both subject only to gravitational forces, their world-lines are by definition straight lines (geodesics). The goal here is to end up with some kind of coordinate grid defining a (t,x) plane, and on such a grid, the two balls' world-lines are vertical lines. If we release them at events P and Q, then observe them again later at R and S, PQRS should form a rectangle on such a plot. In the figure, the irregularly spaced tick marks along the edges of the rectangle are meant to suggest that although ordered geometry provides us with a well-defined ordering along these lines, we have not yet constructed a complete system of measurement.
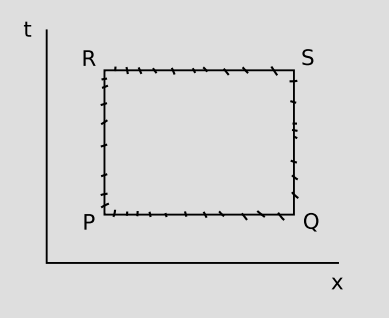
The depiction of PQSR as a rectangle, with right angles at its vertices, might lead us to believe that our geometry would have something like the concept of angular measure referred to in Euclid's E4, equality of right angles. But this is too naive even for the Euclidean 3+1 spacetime of Newton and Galileo. Suppose we switch to a frame that is moving relative to the first one, so that the balls are not at rest. In the Euclidean spacetime, time is absolute, so events P and Q would remain simultaneous, and so would R and S; the top and bottom edges PQ and RS would remain horizontal on the plot, but the balls' world-lines PR and QS would become slanted. The result would be a parallelogram. Since observers in different states of motion do not agree on what constitutes a right angle, the concept of angular measure is clearly not going to be useful here. Similarly, if Euclid had observed that a right angle drawn on a piece of paper no longer appeared to be a right angle when the paper was turned around, he would never have decided that angular measure was important enough to be enshrined in E4.
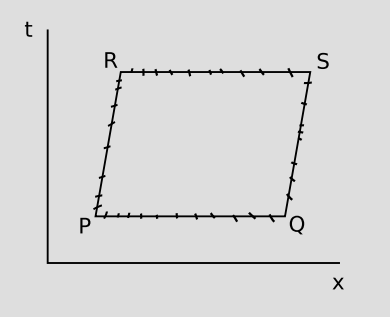
In the context of relativity, where time is not absolute, there is not even any reason to believe that different observers must agree on the simultaneity of PQ and RS. Our observation that time flows differently depending on the observer's state of motion tells us specifically to expect this not to happen when we switch to a frame moving to the relative one. Thus in general we expect that PQRS will be distorted into a form like the one shown in Figure 2.1.3. We do expect, however, that it will remain a parallelogram; a Lorentz frame is one in which the gravitational field, if any, is constant, so the properties of spacetime are uniform, and by symmetry the new frame should still have PR=QS and PQ=RS.
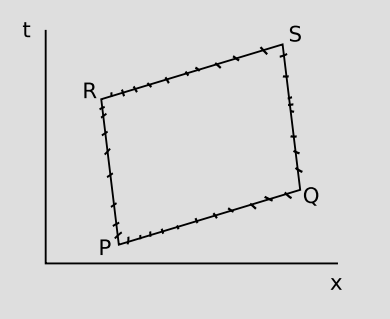
With this motivation, we form the system of affine geometry by adding the following axioms to set O1-O4.1 The notation [PQRS] means that events P, Q, S, and R form a parallelogram, and is defined as the statement that the lines determined by PQ and RS never meet at a point, and similarly for PR and QS.
- A1 Constructibility of parallelograms: Given any P, Q, and R, there exists S such that [PQRS], and if P, Q, and R are distinct then S is unique.
- A2 Symmetric treatment of the sides of a parallelogram: If [PQRS], then [QRSP], [QPSR], and [PRQS].
- A3 Lines parallel to the same line are parallel to one another: If [ABCD] and [ABEF], then [CDEF].
Note
The axioms are summarized for convenient reference in Appendix C. This formulation is essentially the one given by Penrose, The Road to Reality, in section 14.1.
The following theorem is a stronger version of Playfair's axiom E5, the interpretation being that affine geometry describes a spacetime that is locally flat.
- Theorem: Given any line ℓ and any point P not on the line, there exists a unique line through P that is parallel to ℓ.
This is stronger than E5, which only guarantees uniqueness, not existence. Informally, the idea here is that A1 guarantees the existence of the parallel, and A3 makes it unique.2
proof
Pick any two distinct points A and B on ℓ, and construct the uniquely determined parallelogram [ABPQ] (axiom A1). Points P and Q determine a line (axiom O1), and this line is parallel to ℓ (definition of the parallelogram). To prove that this line is unique, we argue by contradiction. Suppose some other parallel m to exist. If m crosses the infinite line BQ at some point Z, then both [ABPQ] and [ABPZ], so by A1, Q=Z, so the ℓ and m are the same. The only other possibility is that m is parallel to BQ, but then the following chain of parallelisms holds: PQ || AB || m || BQ. By A3, lines parallel to another line are parallel to each other, so PQ || BQ, but this is a contradiction, since they have Q in common.
Although these new axioms do nothing more than to introduce the concept of parallelism lacking in ordered geometry, it turns out that they also allow us to build up a concept of measurement. Let ℓ be a line, and suppose we want to define a number system on this line that measures how far apart events are. Depending on the type of line, this could be a measurement of time, of spatial distance, or a mixture of the two. First we arbitrarily single out two distinct points on ℓ and label them 0 and 1. Next, pick some auxiliary point q0 not lying on ℓ. By A1, construct the parallelogram 01q0q1. Next construct q01q12. Continuing in this way, we have a scaffolding of parallelograms adjacent to the line, determining an infinite lattice of points 1, 2, 3, . . . on the line, which represent the positive integers. Fractions can be defined in a similar way. For example, 12 is defined as the point such that when the initial lattice segment 0 12 is extended by the same construction, the next point on the lattice is 1.
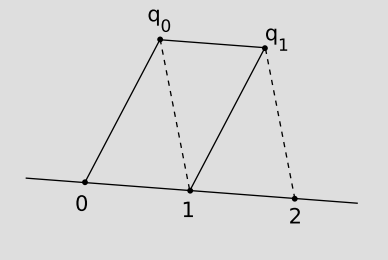
The continuously varying variable constructed in this way is called an affine parameter. The time measured by a free-falling clock is an example of an affine parameter, as is the distance measured by the tick marks on a free-falling ruler. Since light rays travel along geodesics, the wave crests on a light wave can even be used analogously to the ruler’s tick marks.
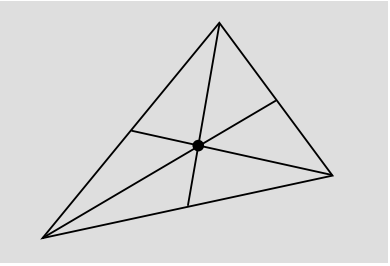
Example 1: centroids
The affine parameter can be used to define the centroid of a set of points. In the simplest example, finding the centroid of two points, we simply bisect the line segment as described above in the construction of the number 12. Similarly, the centroid of a triangle can be defined as the intersection of its three medians, the lines joining each vertex to the midpoint of the opposite side.
Example 2: Conservation of momentum
In nonrelativistic mechanics, the concept of the center of mass is closely related to the law of conservation of momentum. For example, a logically complete statement of the law is that if a system of particles is not subjected to any external force, and we pick a frame in which its center of mass is initially at rest, then its center of mass remains at rest in that frame. Since centroids are well defined in affine geometry, and Lorentz frames have affine properties, we have grounds to hope that it might be possible to generalize the definition of momentum relativistically so that the generalized version is conserved in a Lorentz frame. On the other hand, we don’t expect to be able to define anything like a global Lorentz frame for the entire universe, so there is no such natural expectation of being able to define a global principle of conservation of momentum. This is an example of a general fact about relativity, which is that conservation laws are difficult or impossible to formulate globally.
Although the affine parameter gives us a system of measurement for free in a geometry whose axioms do not even explicitly mention measurement, there are some restrictions:
- The affine parameter is defined only along straight lines, i.e., geodesics. Alice’s clock defines an affine parameter, but Betty’s does not, since it is subject to nongravitational forces.
- We cannot compare distances along two arbitrarily chosen lines, only along a single line or two parallel lines.
- The affine parameter is arbitrary not only in the choice of its origin 0 (which is to be expected in any case, since any frame of reference requires such an arbitrary choice) but also in the choice of scale. For example, there is no fundamental way of deciding how fast to make a clock tick.
We will eventually want to lift some of these restrictions by adding to our kit a tool called a metric, which allows us to define distances along arbitrary curves in space time, and to compare distances in different directions. The affine parameter, however, will not be entirely superseded. In particular, we’ll find that the metric has a couple of properties that are not as nice as those of the affine parameter. The square of a metric distance can be negative, and the metric distance measured along a light ray is precisely zero, which is not very useful.
Exercise 2.2.1
Self-check: By the construction of the affine parameter above, affine distances on the same line are comparable. By another construction, verify the claim made above that this can be extended to distances measured along two different parallel lines.
Example 3: Area and volume
It is possible to define area and volume in affine geometry. This is a little surprising, since distances along different lines are not even comparable. However, we are already accustomed to multiplying and dividing numbers that have different units (a concept that would have given Euclid conniptions), and the situation in affine geometry is really no different. To define area, we extend the one-dimensional lattice to two dimensions. Any planar figure can be superimposed on such a lattice, and dissected into parallelograms, each of which has a standard area.

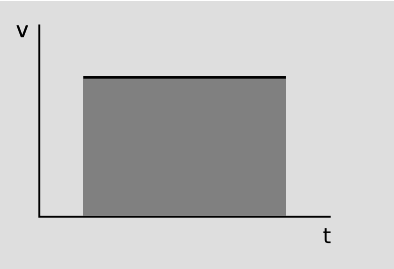
Example 4: Area on a graph of v versus t
If an object moves at a constant velocity v for time t, the distance it travels can be represented by the area of a parallelogram in an affine plane with sides having lengths v and t. These two lengths are measured by affine parameters along two different directions, so they are not comparable. For example, it is meaningless to ask whether 1 m/s is greater than, less than, or equal to 1 s. If we were graphing velocity as a function of time on a conventional Cartesian graph, the v and t axes would be perpendicular, but affine geometry has no notion of angular measure, so this is irrelevant here.
Exercise 2.2.2
Self-check: If multiplication is defined in terms of affine area, prove the commutative property ab = ba and the distributive rule a(b + c) = ab + bc from axioms A1-A3.


