18.2: The Velocity Curve from the Elements
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we calculate the velocity curve (i.e. how the radial velocity varies with time) to be expected from a star with given orbital elements. Of course, the practical situation is quite the opposite: we observe the velocity curve, and from it, we wish to determine the elements. We’ll deal with that later.
I’m going to use the convenient phrase “plane of the sky” to mean a plane tangent to the celestial sphere, or normal to the line of sight from observer to the centre of mass of the system. The centre of mass C of the system, then, is stationary in the plane of the sky. The plane of the orbits of the two stars around their centre of mass is inclined at an angle i to the plane of the sky. I am going to follow the adventures of star 1 about the centre of mass C. And I am going to assume that Chapter 9 is all fresh in your mind!
The semi major axis of the orbit of star 1 about C is a1, and the semi latus rectum l1=a1(1−e2). The angular momentum per unit mass of star 1 about C is r21˙v=√GMl1, where v is the true anomaly and M=m32/(m1+m2)2. The orbital period P is given by P2=4π2GMa31. The mean motion n is 2p/P, and hence n2 a13 = GM. Therefore the angular momentum per unit mass is
r21˙v=na21√1−e2.
In figure XVIII.1 we see the star 1 (labelled S) in orbit around C, and at some time the argument of latitude of S is θ, and its distance from C is r1. Its distance above the plane of the sky is z, and r1 sin β. The inclination of the plane of the orbit to the plane of the sky is i, and, in order to find an expression for β in terms of the argument of latitude and the inclination, I’m just going to draw, in figure VIII.2, these angles on the surface of a sphere. The sphere is centred at C, and is of arbitrary radius.
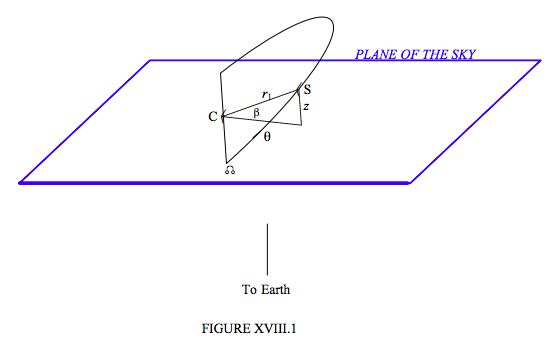
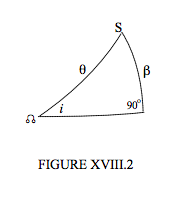
We see from this triangle that sin β = sin i sin θ. Also, the argument of latitude θ = ω + v, (ω = argument of periastron, v = true anomaly), and so
z=r1sinisin(ω+v).
At this moment, the radial velocity V of star 1 relative to the Sun is given by
V=V0+˙z,
where V0 is the radial velocity of the centre of mass C, or the systemic velocity. Differentiation of Equation 18.2.1 with respect to time gives
˙z=sin[˙r1sin(ω+v)+r1˙vcos(ω+v)].
I would like to express this entirely in terms of the true anomaly v instead of v and r1. The Equation to the ellipse is
r1=l11+ecosv=a1(1−e2)1+ecosv,
where l1 is the semi latus rectum, and so
˙r1=l1e˙vsinv(1+ecosv)2=r1e˙vsinv1+ecosv.
which helps a bit. Thus we have
˙zsini=r1˙v(esinvsin(ω+v)1+ecosv+cos(ω+v)).
We can also make use of Equation 18.2.1, and, with some help from Equation 18.2.5, we obtain
˙zsini=na1(1+ecosv)√1−e2(esinvsin(ω+v)1+ecosv+cos(ω+v))
or
˙zsini=na1√1−e2(esinvsin(ω+v)+(1+ecosv)cos(ω+v)).
Now esin v sin(ω + v) + e cosvcos(ω + v) = e cosω,so we are left with
˙z=na1sini√1−e2(cos(ω+v)+ecosω).
The quantity na1sini√1−e2, which has the dimensions of speed, is generally given the symbol K1, so that
˙z=K1(cos(ω+v)+ecosω),
and so the radial velocity (including the systemic velocity) as a function of the true anomaly and the elements is given by
V=V0+K1(cos(ω+v)+ecosω).
You can see that ˙z varies between K1(1 e cos ω) and -K1(1 - e cos ω), and that K1 is the semi-amplitude of the radial velocity curve.
Equation 18.2.12 gives the radial velocity as a function of the true anomaly. But we really want the radial velocity as a function of the time. This is easy, or at least straightforward, because we already know how to calculate the true anomaly as a function of time. I give here the relevant Equations. I have retained their original numbering, so that you can locate them in the earlier chapters.
M=2πP(t−T)
M=E−esinE
cosv=cosE−e1−ecosE
From trigonometric identities, this can also be written
sinv=√1−e2sinE1−ecosE
or
tanv=√1−e2sinEcosE−e
or
tan12v=√1+e1−etan12E
I show in figures XIII.3 and XIII.4 two examples of velocity curves. Figure XIII.3 is computed for e = 0.5, ω = 0o. Figure XIII.4 is computed for e = 0.75, ω = 90o.
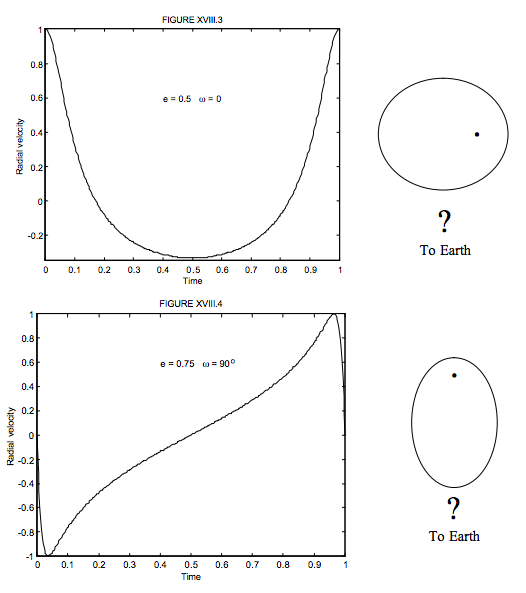
In order to draw these two figures, it will correctly be guessed that I have written a computer program that will calculate Equations 9.6.4, 9.6.5, 2.3.16 and 18.2.12 in order, for the chosen values of e and ω. This is perfectly straightforward except that Equation 9.6.5, Kepler’s Equation, requires some iteration. The solution of Kepler’s Equation was discussed in Section 9.6. If I were seriously going to be interested in computing the orbits of spectroscopic binary stars I would at this stage use this program to generate and print out 360 radial velocity curves for 36 values of ω going from 0o to 350o and ten value of e going from 0.0 to 0.9. Then, when I had a real radial velocity curve of a real spectroscopic binary star to analyse, I would be able to compare it with my set of theoretical curves and hence be able to get a least a rough first approximation to the eccentricity and argument of periastron.
I have drawn figures XVIII.3 and 4 for a systemic velocity V0 of zero. A real star will not have a zero systemic velocity and indeed one of the aims must be to determine the systemic velocity.
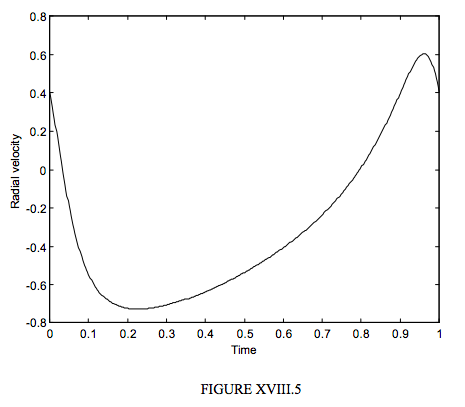
Thus in figure XVIII.5 I have drawn a radial velocity curve (I’m not saying what the values of ω and e are), but this time I have not assumed a zero systemic radial velocity. It will be noticed that the observed star spends much longer moving towards us than away from us. If we draw a horizontal line Radial Velocity = V0 across the figure, this line must be drawn such that the area between it and the radial velocity curve above it is equal to the area between it and the radial velocity curve below it. How to position this line? That is a good question. If nothing else, you can count squares on graph paper. That at least will give you a first rough idea of what the systemic velocity is.
If you have a double-lined binary, you will have two radial velocity curves. They are not quite mirror images of each other; the semiamplitude of each component is inversely proportional to its mass. But the systemic velocity is then easy, because the two curves cross when the radial velocity of each is equal to the radial velocity of the system.


